Метод наименьших квадратов и его приложения

Актуальность исследования
Большая часть задач в приложениях сводится к линейной задаче метода наименьших квадратов. Например, задача определения параметров орбитальных параметров космического корабля. Эти параметры оцениваются методом наименьших квадратов.
Многие экономические исследования основываются на математических понятиях и теоремах.
Широко применяется метод наименьших квадратов в корреляционно-регрессионном анализе, когда ставится цель дать количественное описание взаимосвязей между экономическими переменными.

Структура работы
ВВЕДЕНИЕ
ГЛАВА 1 ПАРНАЯ РЕГРЕССИЯ
ГЛАВА 2 МНОЖЕСТВЕННАЯ РЕГРЕССИЯ
ЗАКЛЮЧЕНИЕ
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ

В первой главе приведены основные понятия необходимые для теоретического изложения изучаемой темы, даны определения парной регрессии и корреляционной зависимости. Дана оценка параметров уравнения линейной парной регрессии с помощью метода наименьших квадратов, строится уравнение регрессии. Дается оценка значимости уравнения парной линейной регрессии в целом и по параметрам. Показано, как уравнение регрессии может быть использовано при прогнозировании. В последнем параграфе рассматривается криволинейная корреляция, приводятся методы линеаризации этих моделей, дается оценка параметров и уравнения регрессии.
Изложение теоретического материала сопровождается практическими задачами.

Во второй главе рассмотрена модель множественной линейной регрессии, для которой выполняются условия Гаусса-Маркова. Рассмотрены вопросы отбора факторов линейной регрессии. Дана оценка параметров уравнения множественной регрессии с помощью метода наименьших квадратов. Построены частные уравнения регрессии, которые связывают результативный признак с соответствующими факторами при закреплении других факторов, учитываемых в уравнении множественной регрессии на среднем уровне. Оценивается практическая значимость уравнения множественной регрессии с помощью показателя множественной корреляции и коэффициента детерминации.
Приведено достаточно большое число практических задач.

В работе рассмотрена, например, задача
Задача. Имеются следующие данные о розничном товарообороте магазина за первое полугодие:
Используя аналитическое выравнивание по прямой, определить объем товарооборота за июль.

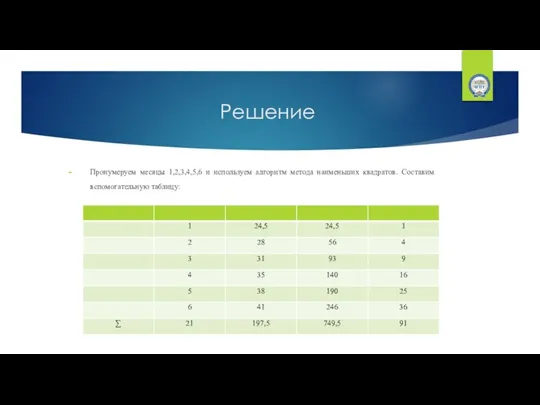
Решение
Пронумеруем месяцы 1,2,3,4,5,6 и используем алгоритм метода наименьших квадратов. Составим вспомогательную таблицу:

Заключение
Задачи, рассмотренные в работе, поставлены самостоятельно, дана интерпретация результатов. Показано, что знание экономики, а тем более управление ею, невозможно без знания математики. Стремительное развитие экономики потребовало использования вероятностно-статистических методов и математического моделирования. Правильно построенная модель позволяет контролировать экономическую ситуацию на достоверном анализе имеющихся данных, разработать варианты перспективного развития предприятия.
В данной работе изложены общематематические основы количественного анализа различных процессов, что даёт возможность применять их в практической деятельности руководителя, бухгалтера, маркетолога.