Содержание
- 2. Обратные тригонометрические функции
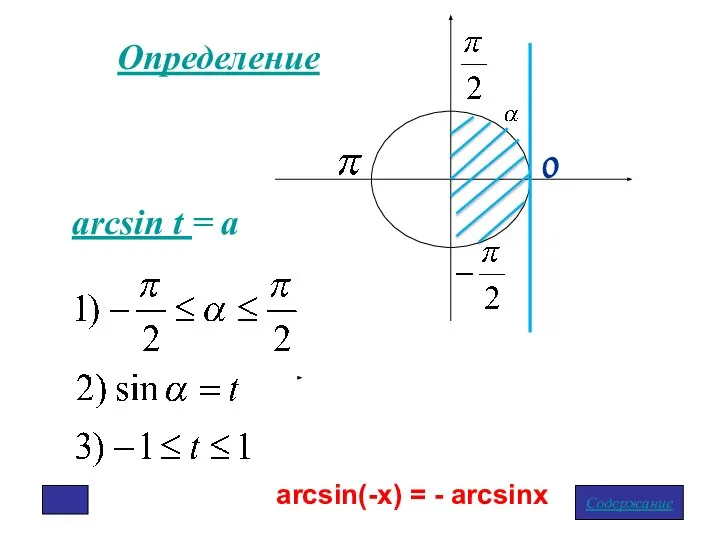
- 3. Определение arcsin t = a arcsin(-x) = - arcsinx Содержание
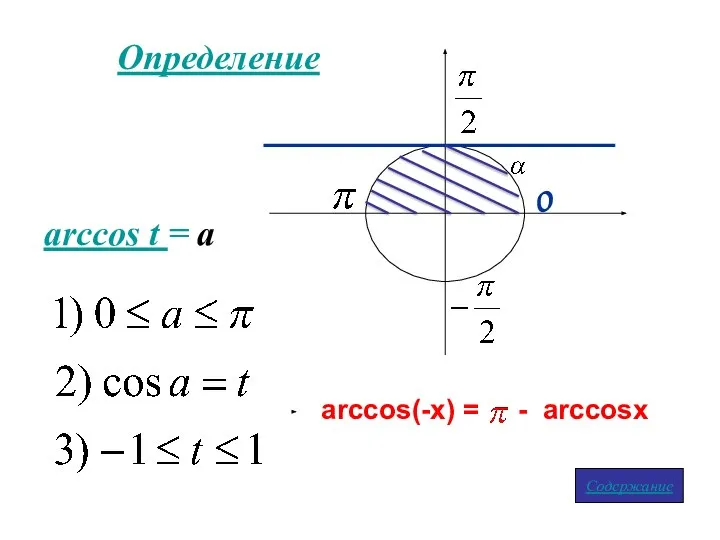
- 4. Определение arccos t = a Содержание arccos(-x) = - arccosx
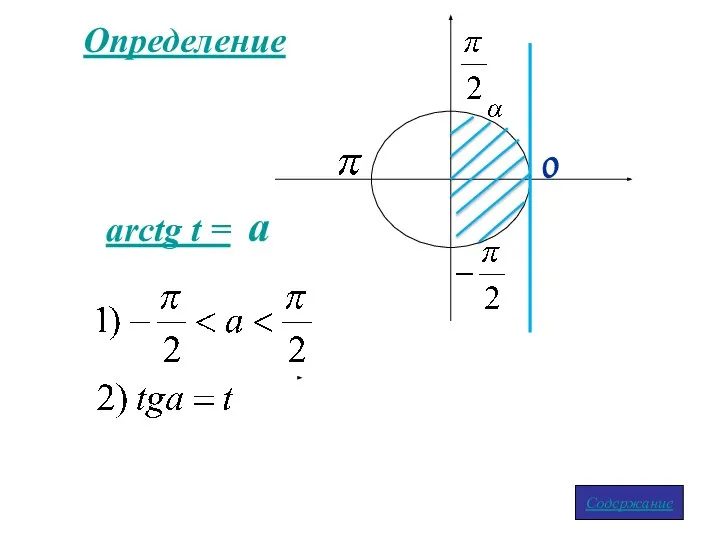
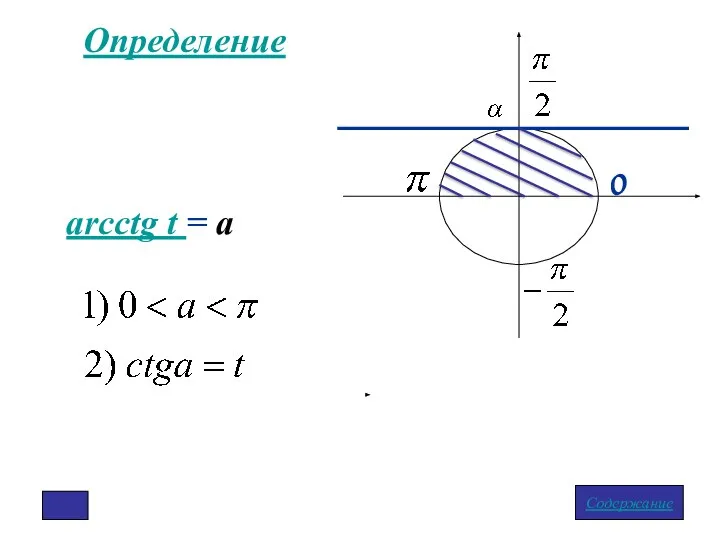
- 5. Определение arctg t = a Содержание
- 6. Определение arcctg t = a Содержание
- 7. у = arcsinx Содержание х 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок ; 3)Функция у
- 8. у=arccos x Содержание 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция у = arcсos x
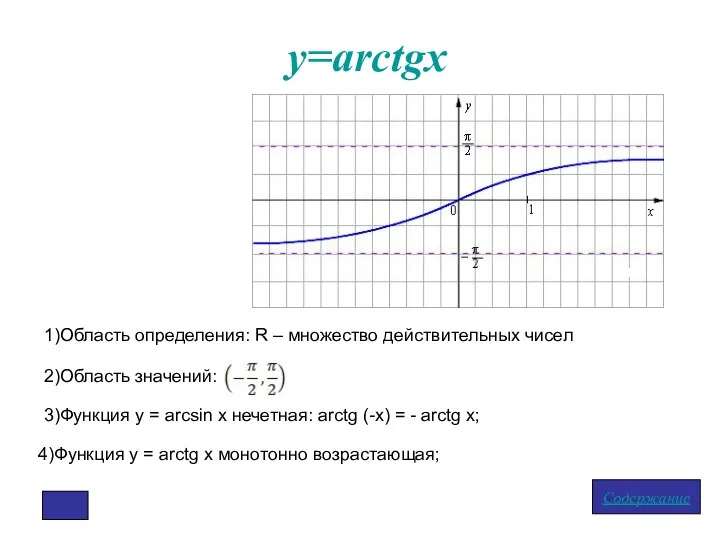
- 9. у=arctgx Содержание 1)Область определения: R – множество действительных чисел 2)Область значений: 3)Функция у = arcsin x
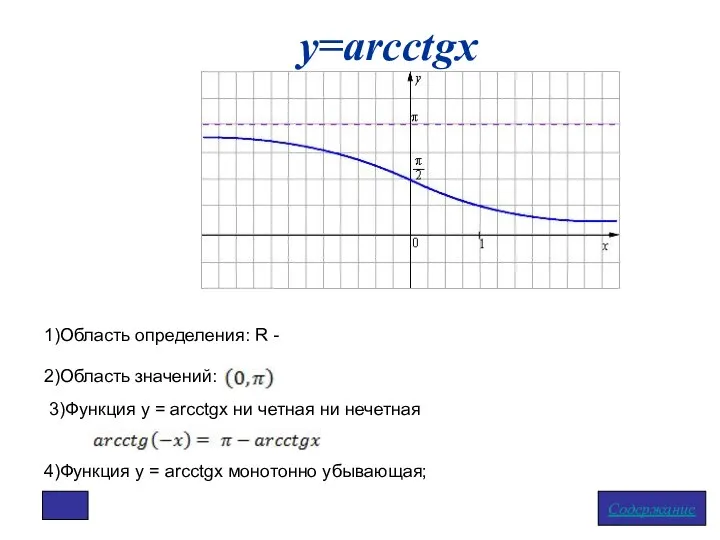
- 10. у=arcctgx Содержание 1)Область определения: R - 2)Область значений: 4)Функция у = arcсtgx монотонно убывающая; 3)Функция у
- 11. Свойства аркфункций
- 13. Скачать презентацию
![у = arcsinx Содержание х 1)Область определения: отрезок [-1; 1]; 2)Область значений:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/975284/slide-6.jpg)
![у=arccos x Содержание 1)Область определения: отрезок [-1; 1]; 2)Область значений: отрезок 3)Функция](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/975284/slide-7.jpg)

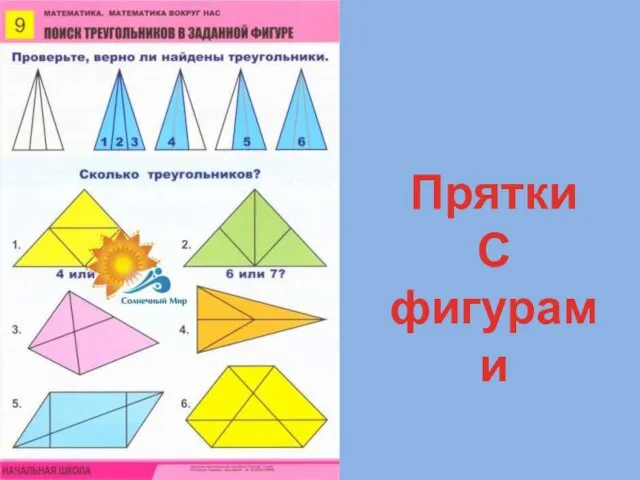 Прятки с фигурами
Прятки с фигурами Презентация на тему Итоговый урок: решение систем уравнений
Презентация на тему Итоговый урок: решение систем уравнений  Последние цифры степеней
Последние цифры степеней Решение алгебраических и трансцендентных уравнений
Решение алгебраических и трансцендентных уравнений Анализ уравнений регрессии с помощью двумерных сечений поверхностей отклика
Анализ уравнений регрессии с помощью двумерных сечений поверхностей отклика Прямоугольник. Свойства прямоугольника
Прямоугольник. Свойства прямоугольника Геометрическая прогрессия
Геометрическая прогрессия Великие математики древности
Великие математики древности Квадратичная функция проверочная работа
Квадратичная функция проверочная работа Деление
Деление Арифметичская прогрессия
Арифметичская прогрессия Верхняя, нижняя сумма Дарбу
Верхняя, нижняя сумма Дарбу На оптимизацию с решением
На оптимизацию с решением Математика в профессиях
Математика в профессиях Цилиндр. Шар. Задачи по геометрии
Цилиндр. Шар. Задачи по геометрии Графики функций. Зачет
Графики функций. Зачет Цели урока:
Цели урока: Уравнения, системы уравнений. Задание №9
Уравнения, системы уравнений. Задание №9 Квадратичная функция
Квадратичная функция Вписанная и описанная окружности
Вписанная и описанная окружности Задача 3. Построить матрицу поворота
Задача 3. Построить матрицу поворота Математические этюды
Математические этюды Применение метода интервалов для решения неравенств. 8 класс
Применение метода интервалов для решения неравенств. 8 класс Решение логарифмических уравнений
Решение логарифмических уравнений Добери знак
Добери знак Решение текстовых задач арифметическим способом
Решение текстовых задач арифметическим способом Прямоугольная система координат в пространстве
Прямоугольная система координат в пространстве Метод коэффициентов
Метод коэффициентов