Слайд 2Повторение.
Регрессионный анализ
Регрессионный анализ — статистический метод исследования зависимости между зависимой переменной Y и одной или несколькими независимыми переменными X1,X2,...,Xp.

Слайд 3Этапы получения регрессионной модели
Подбор вида функции
Вычисления параметров функции
График регрессионной модели называется трендом

Слайд 4Задача подбора вида функции
Не имеет строго решения. Перебор из конечного числа функций

и выбор лучшей из них; успех решения данной задачи зависит от опыта и интуиции исследователя.
Слайд 5Задача подбора вида функции. Виды функций.
y=a∙x+b – линейная функция
y=a ∙ x2+b ∙

x+c – квадратичная функция
y=a ∙ ln(x)+b– логарифмическая функция
y=a ∙ eb∙x– экспоненциальная функция
y=a ∙ xb– степенная функция
x– аргумент, y– значение функции, a, b, c, d– параметры функции
Слайд 6Вычисления параметров функции. Метод наименьших квадратов (18 век, математик К. Гаус)
Нужно подобрать

параметры функции (a, b, c и пр.) так, чтобы функция располагалась как можно ближе к экспериментальным точка.
Искомая функция должна быть построена так, чтобы сумма квадратов отклонений y-координат всех экспериментальных точек от y-координат графика функции была минимальной.
R2 – коэффициент детерминированности. 0
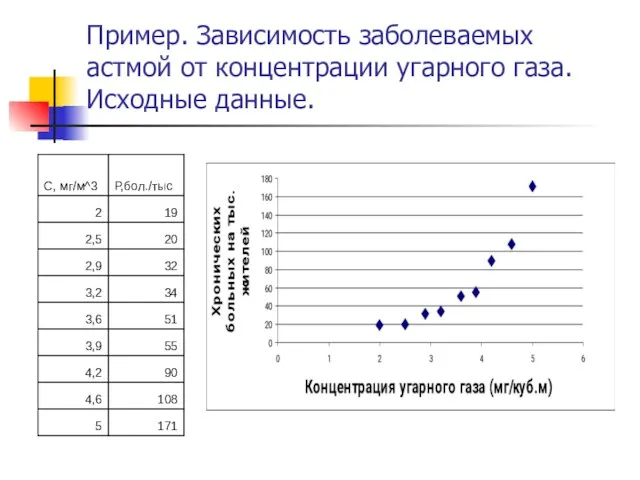
Слайд 7Пример. Зависимость заболеваемых астмой от концентрации угарного газа. Исходные данные.
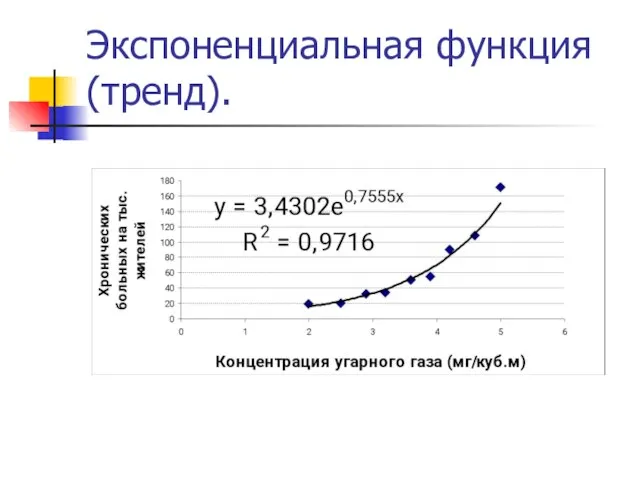
Слайд 8Экспоненциальная функция (тренд).
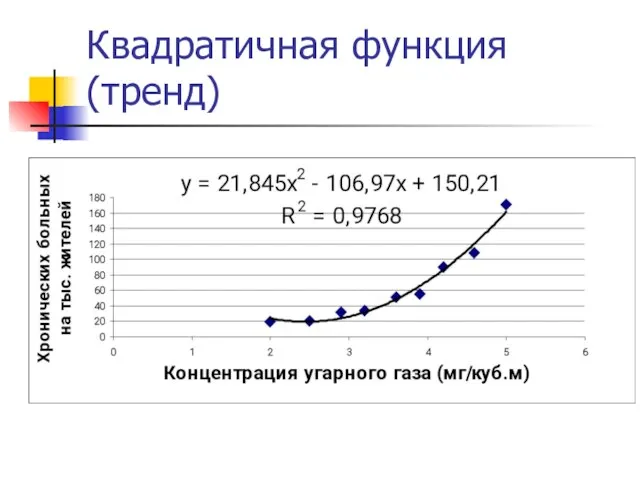
Слайд 9Квадратичная функция (тренд)








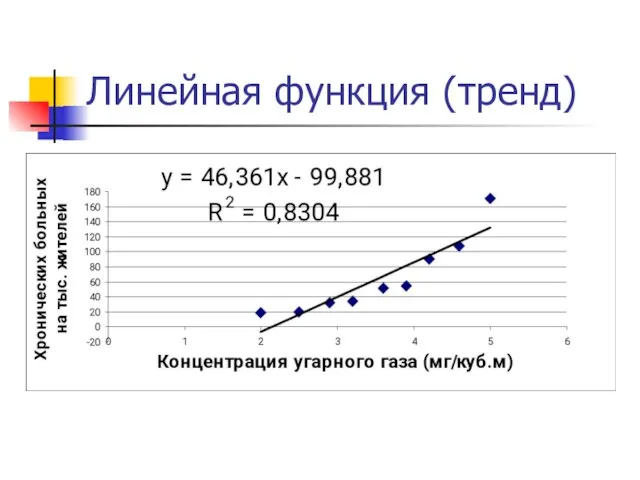
 Ветер истории дует- Он развернул паруса… Видится замок Артура, Леди Гиневы глаза…
Ветер истории дует- Он развернул паруса… Видится замок Артура, Леди Гиневы глаза… Особенности суицида в разные возрастные периоды
Особенности суицида в разные возрастные периоды Бур лун
Бур лун ПРАВИЛЬНЫЕ МНОГОГРАННИКИ
ПРАВИЛЬНЫЕ МНОГОГРАННИКИ Изделия из теста
Изделия из теста Рисунок кистей рук
Рисунок кистей рук Презентация на тему Мораль и нравственность
Презентация на тему Мораль и нравственность Проверяем знания
Проверяем знания Функциональная схема компьютера
Функциональная схема компьютера  Методы маркетинга персонала
Методы маркетинга персонала investitsii_5
investitsii_5 Колбасные кейсы. Проведения промо-акции с нестандартным подходом к тестированию продукции
Колбасные кейсы. Проведения промо-акции с нестандартным подходом к тестированию продукции «Есть в озере Псковском три острова чудных…»
«Есть в озере Псковском три острова чудных…» The Big Bang Social Theory!
The Big Bang Social Theory! Mother’s Day part2
Mother’s Day part2 Презентация на тему Книжный червь Bookworms
Презентация на тему Книжный червь Bookworms Сердце милая сторонка
Сердце милая сторонка Маркетинговые исследования в рекреационной сфере Крыма
Маркетинговые исследования в рекреационной сфере Крыма Последовательная обработка данных
Последовательная обработка данных  МЕДИЦИНСКАЯ РЕАБИЛИТАЦИЯ ДЕТЕЙ С АПЛАСТИЧЕСКИМИ АНЕМИЯМИ
МЕДИЦИНСКАЯ РЕАБИЛИТАЦИЯ ДЕТЕЙ С АПЛАСТИЧЕСКИМИ АНЕМИЯМИ Соломон
Соломон Презентация на тему Озеро Тургояк (Миасс)
Презентация на тему Озеро Тургояк (Миасс)  Правила процедуры
Правила процедуры Верстальщик
Верстальщик Экологическое право
Экологическое право Презентация на тему США 1945-1963
Презентация на тему США 1945-1963  Вологодский филиал РАНХиГС
Вологодский филиал РАНХиГС Презентация по английскому my animals 2 класс
Презентация по английскому my animals 2 класс