Метод переменных состояния

Уравнения состояния в матричной форме
1

Где [X'(t)] – матрица-столбец производных от токов в индуктивностях и напряжений в емкостях (n - элементов)

[A] – квадратная матрица коэффициентов при переменных состояния (n – строк и n – столбцов)

[X(t)] – матрица-столбец переменных состояния (n – элементов)

[F(t)] – матрица-столбец (независимых) источников ЭДС и тока (m – элементов)

[B] – прямоугольная матрица связи, состоящая из коэффициентов перед источниками ЭДС и тока
(n – строк, m – столбцов)

Алгебраические уравнения для выходных величин в матричной форме
2

Где [Y(t)] – матрица-столбец выходных величин (k - элементов)

[С] – прямоугольная матрица связи выходных величин с переменными состояния (k – строк, n – столбцов)

[D] – прямоугольная матрица связи выходных величин с источниками (k – строк, m – столбцов)

Порядок расчета

1. Из расчета схемы до коммутации определяются ННУ

2. Для схемы после коммутации по законам Кирхгофа составляем уравнения и
2
1

3. По специальным программам на ЭВМ решаем уравнения и
2
1
и получаем численные значения для Y(t)

Пример

Дано:
Определить:

1. Определяем независимые начальные условия:

2. По теореме компенсации заменим реактивные элементы источниками:
индуктивность – источником тока
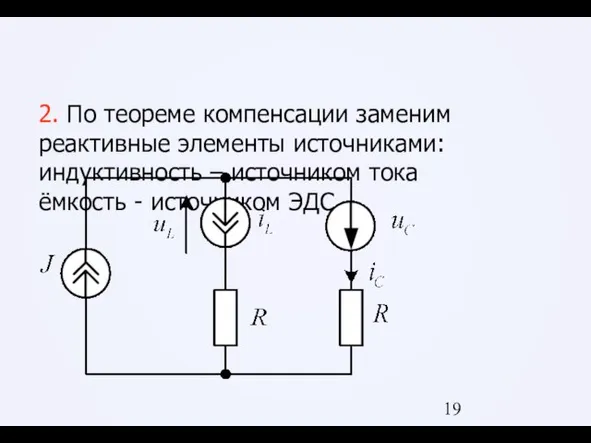
ёмкость - источником ЭДС

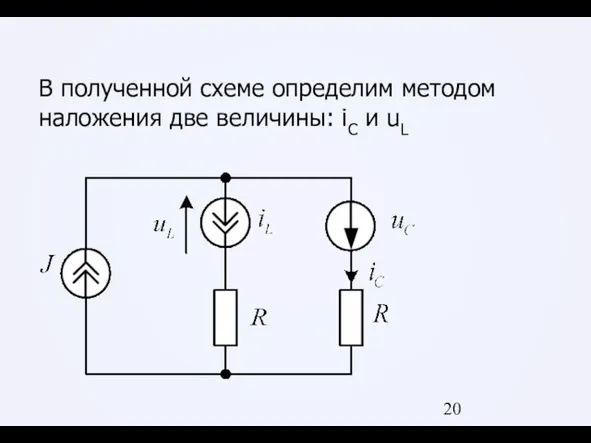
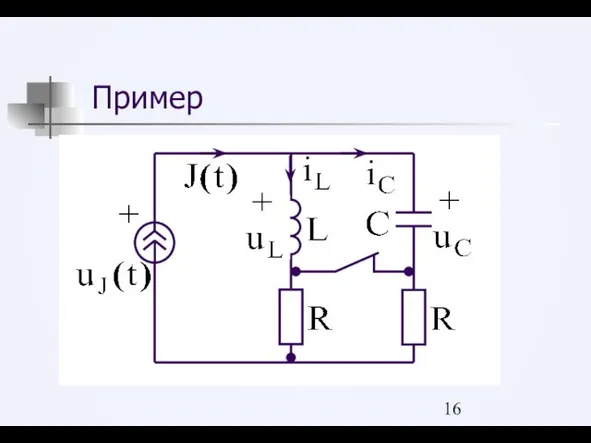
В полученной схеме определим методом наложения две величины: iC и uL

В соответствии с методом наложения:
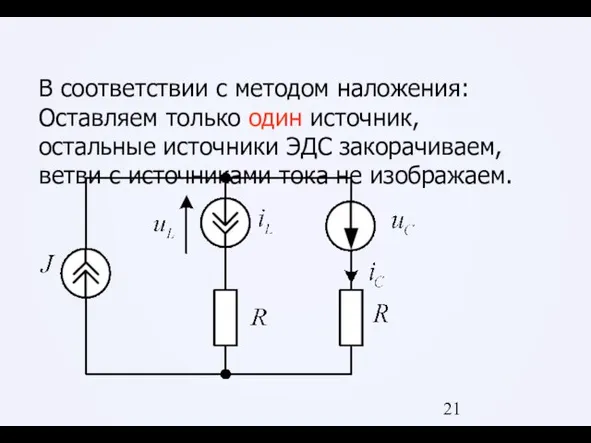
Оставляем только один источник, остальные источники ЭДС закорачиваем, ветви с источниками тока не изображаем.

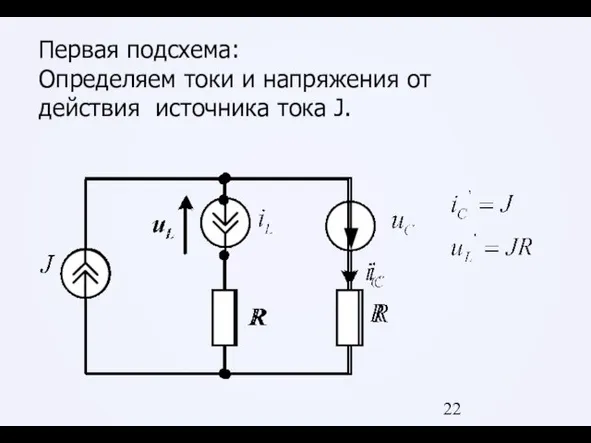
Первая подсхема:
Определяем токи и напряжения от действия источника тока J.

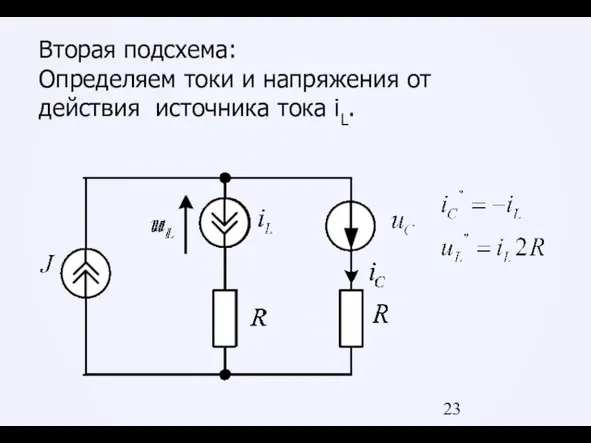
Вторая подсхема:
Определяем токи и напряжения от действия источника тока iL.

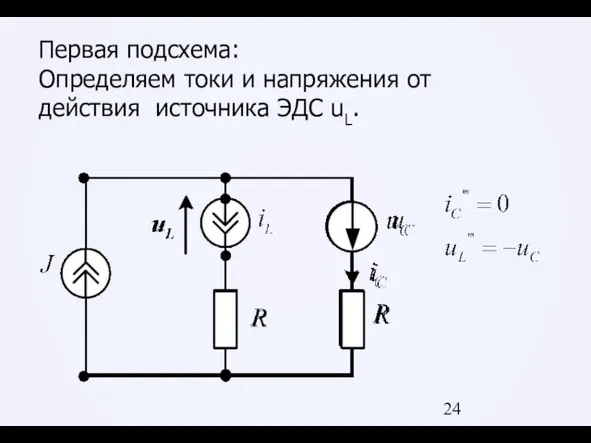
Первая подсхема:
Определяем токи и напряжения от действия источника ЭДС uL.

Примечание: для MATHCAD