Метод рационализации при решении показательных и логарифмических неравенств

Прежде чем говорить о методе рационализации в логарифмических и показательных неравенствах непосредственно, несколько слов о том, почему эта тема актуальна при подготовке к ЕГЭ.
Рассмотрим логарифмическое неравенство вида , где h,f,g- некоторые функции от х.

Стандартный метод решения такого неравенства предполагает разбор двух случаев на области допустимых значений неравенства.
В первом случае, когда основания логарифмов удовлетворяют условию
, знак неравенства обращается: .
Во втором случае, когда основания удовлетворяет условию
знак неравенства сохраняется: .
На первый взгляд – все логично, рассмотрим два случая и потом объединим ответы. Правда, при рассмотрении второго случая приходится на 90 процентов повторять выкладки из первого случая (преобразовывать, находить корни вспомогательных уравнений, определять промежутки монотонности знака). Возникает естественный вопрос – можно ли все это как-нибудь объединить, тем самым сократив время на решение задачи, что актуально для экзамена, и при этом существенно упростить вычисления? Ответ на этот вопрос и даёт метод рационализации.

Метод рационализации позволяет перейти от неравенства содержащего сложные логарифмические и показательные выражения к равносильному ему рациональному неравенству.
Метод используется при решении неравенств с переменным основанием логарифма и позволяет решать неравенства такого вида без перехода к равносильной совокупности систем, решение которой является достаточно трудоёмким и требующим большого количества времени.
Рассмотрим таблицы, позволяющие рационализировать логарифмические неравенства(заметим, что рационализация производится на ОДЗ)

Таблица работает при условии :f›0,g›0,h›0,h≠1
где f и g— функции от х,
h— функция или число,
V— один из знаков ≤,›,≥,‹
Заметим также, вторая и третья строчки таблицы — следствия первой.
Метод рационализации в логарифмических неравенствах

И еще несколько полезных следствий :
где f и g — функции от x,
h— функция или число,
V— один из знаков ‹,≥,≤,›

Пример 1:

Пример 2:

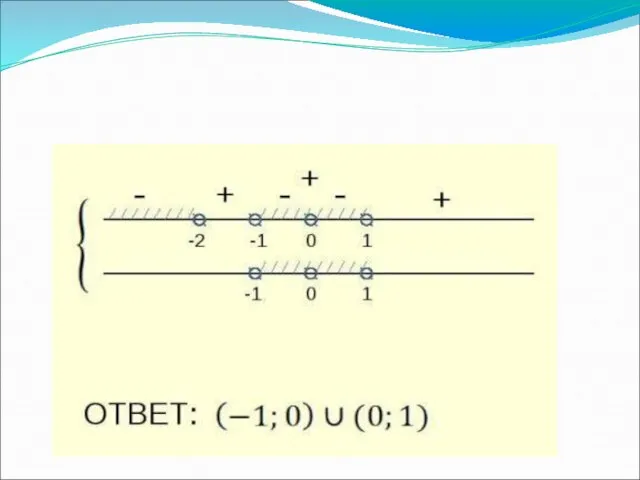
Задание для решения с доской:
Ответ:(0;0,5) U [2;3]

Рассмотрим таблицы, позволяющие рационализировать показательный неравенства .
Таблица для рационализации в показательных неравенствах:
f и g— функции от x, h— функция или число, V— один из знаков ›,≤,≥,‹.Таблица работает при условии h›0,h≠1.
Опять же, по сути, нужно запомнить первую и третью строчки таблицы. Вторая строка -частный случай первой, а четвертая строка — частный случай третьей.

Пример:
(x2-x-2)2x-6 ≥ (x2-x-2)3-4x
X2-x-2›0
х2-x-2 ≠1
((X2-x-2)-1)((2x-6)-(3-4x))≥ 0
x›2
x‹-1
(x2-x-3)(6x-9)≥0 , , ,x2= , x3=1,5
,

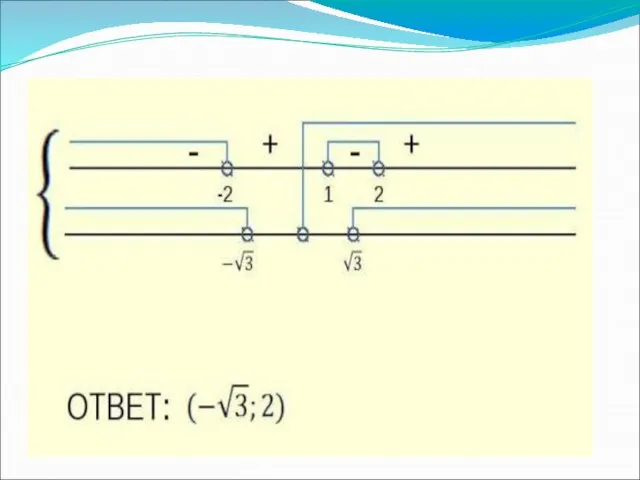
Упорядочим корни:
Так как 3‹ √­­­13 ‹4,то x2‹x3‹x1
С учётом ОДЗ получаем: ( ; -1)U( ; +∞)

Устное упражнение: назвать чему равносильно данное неравенство без учёта ОДЗ
1.logx-3(x2+3x-4)≤ logx-3(5-x)
2.(x-3)x-4 ≤
Далее рассмотрим пример решения системы неравенств:

Решение.
1.Решим первое неравенство:
2. Решим второе неравенство при всех х
При условиях и получаем неравенство
При указанных условиях получаем:
3. Решением системы является общая часть решений двух неравенств.

Так как имеем откуда получаем решение системы.
Ответ: