Содержание
- 2. Строковые метрики Расстояние Хэмминга Расстояние Левенштейна Расстояние Дамерай-Левенштейна, Метрика Нидлмана-Вунша, Метрика Смита-Вотермана Bag distance Метрики Jaro,
- 3. Операции преобразования строк Подстановка kill bill Вставка kill skill Удаление fear ear
- 4. 1. Расстояние Хэмминга (подстановка) dH(GCAT,CGAT) = 2 2. Расстояние Левенштейна (удаление, вставка, подстановка) dE(CGACG, GTCGA) =
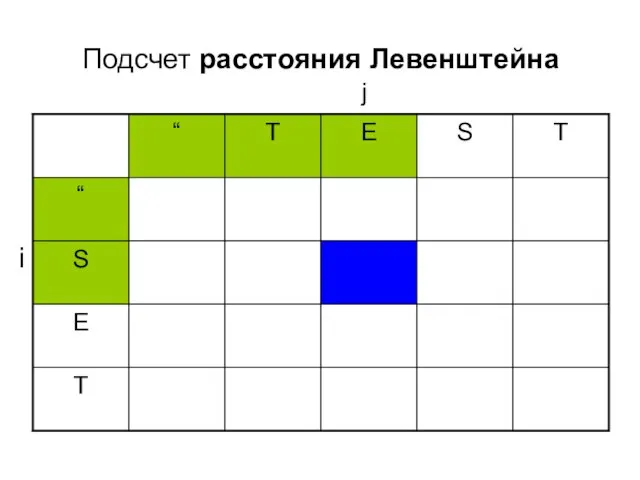
- 5. Подсчет расстояния Левенштейна i j
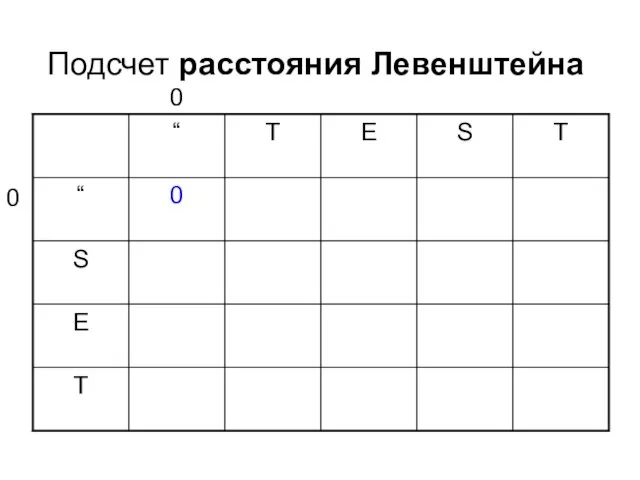
- 6. Подсчет расстояния Левенштейна 0 0
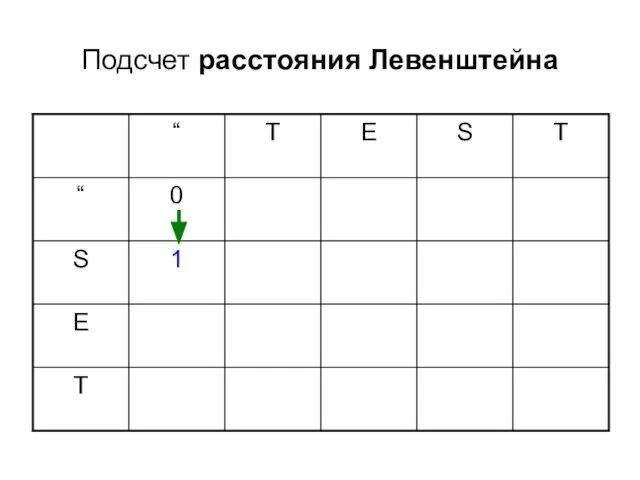
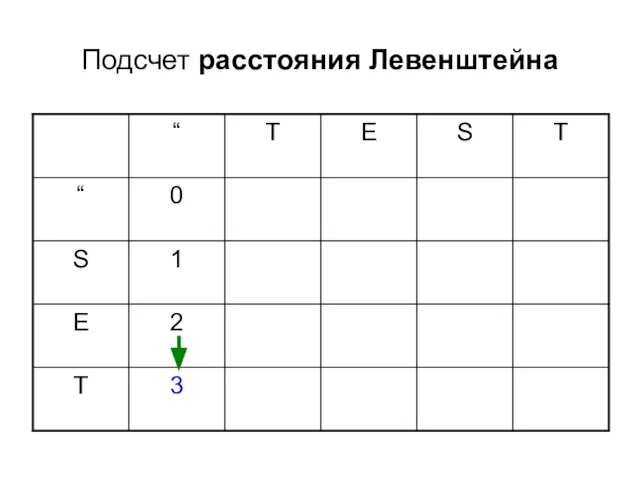
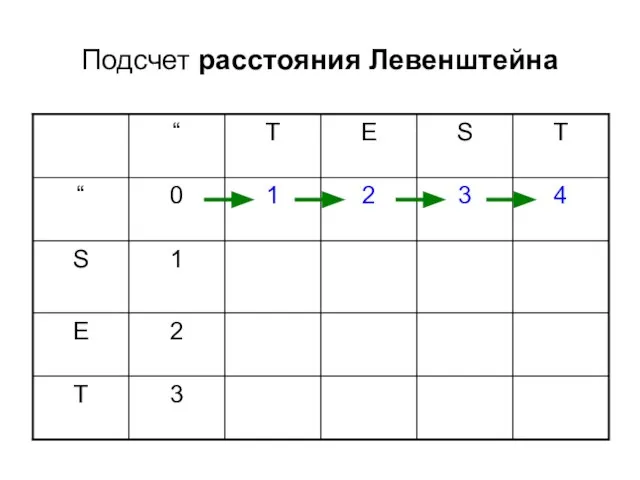
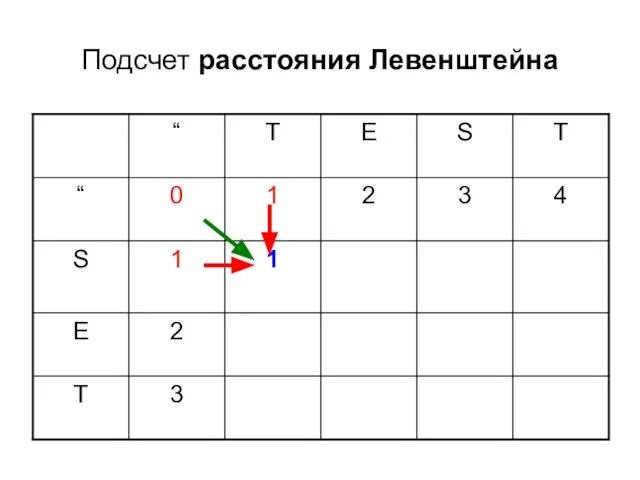
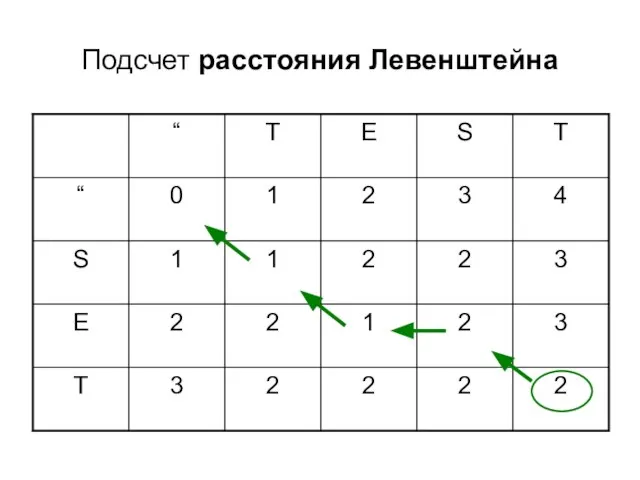
- 7. Подсчет расстояния Левенштейна
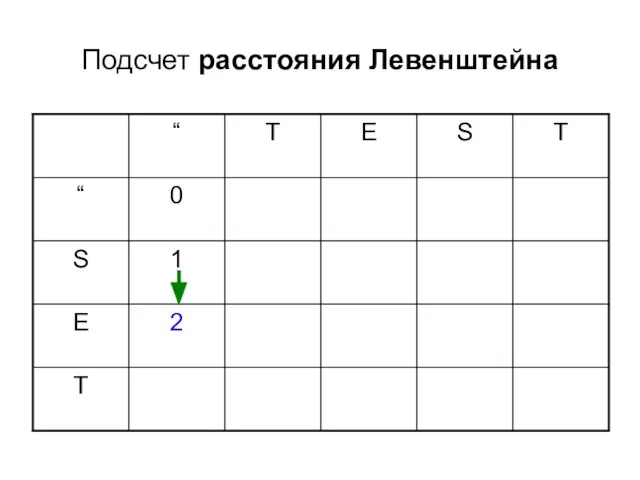
- 8. Подсчет расстояния Левенштейна
- 9. Подсчет расстояния Левенштейна
- 10. Подсчет расстояния Левенштейна
- 11. Подсчет расстояния Левенштейна
- 12. Подсчет расстояния Левенштейна
- 13. Расстояние Дамерау-Левенштейна (перестановка соседних символов) dDL(GCAT,CGAT) = 1 Метрика Нидлмана-Вунша (за операции вставки, удаления, подстановки можно
- 14. Штраф за пропуски Константный штраф dC(“gov”, “government”) = 3 Линейный штраф dL(“gov”, “government”) = 3 *
- 15. Bag distance (Bartolini, 2002)
- 16. Bag distance metric s = “bread” t = “beer” M(s) = {‘b’,‘r’,‘e’,‘a’,‘d’} M(t) = {‘b’,‘e’,‘e’,‘r’} M(s)
- 17. Jaro metric (Winkler, 1999) J(s,t) = ⅓*(Is’I/IsI + It’I/ItI + (Is’I – [Ts’,t’ /2])/Is’I) s =
- 18. Jaro metric (Winkler, 1999) Общие символы ai = bj R = [max(IsI,ItI)/2] - 1 s t
- 19. Jaro metric 1. s = “CRETA” t = “TRACES” 2. R = [max(|s|, |t|)/2] – 1
- 20. Jaro-Winkler metric JW(s,t) = J(s,t) + α* boost(s,t)*(1-J(s,t)) boost(s,t) = min( ILcp(s,t)I, p) s = “DIXON”
- 21. q-grams metric (Gravano, 2001) q-gram – подстрока заданной строки длины q s = “MARTHA” q =
- 22. q-grams metric s = “MARTHA” t = “MARCH” G2(s) = { “#M”,“MA”, “AR”, “RT”, “TH”, “HA”,
- 23. Skip-gram metric (Keskustalo, 2003) Skip-gram – “q-грамма”, которая может состоять из несоседних символов s = “MARTHA”
- 24. Общий префикс(Common Prefix) 2 CPα(s,t) = (|Lcp(s,t)| + α) / (|s| * |t|) s = “MARTHA”
- 25. Наибольшая общая подстрока 0, |Lcs(s,t)| |Lcs(s,t)| + LCS(s-Lcs(s,t), t-Lcs(s,t)) s = “abcdeftg” t = “bcdaefg” k
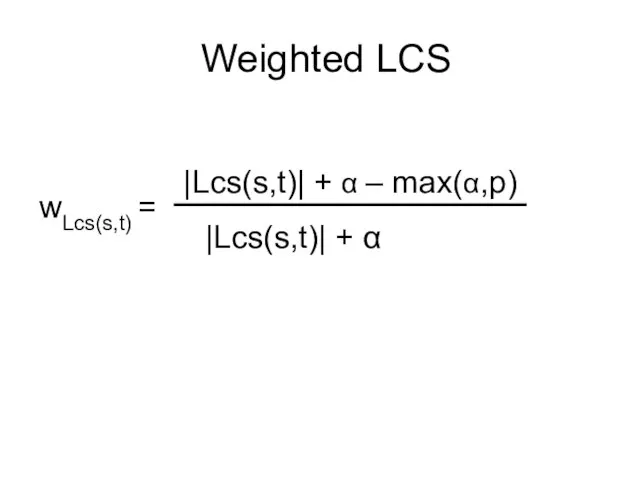
- 26. Weighted LCS |Lcs(s,t)| + α – max(α,p) |Lcs(s,t)| + α wLcs(s,t) =
- 27. Monge-Elkan (Monge and Elkan, 1996) s = {s1s2..sK} t = {t1t2..tL} Monge-Elkan(s,t) = 1/K * Ʃ
- 28. Наборы тестирующих данных Польские имена (1457) Полные польские имена (1219)
- 29. Результаты исследования
- 31. Скачать презентацию








![Jaro metric (Winkler, 1999) Общие символы ai = bj R = [max(IsI,ItI)/2] - 1 s t](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/460318/slide-17.jpg)










 Модерн
Модерн Художественные работы
Художественные работы www.marketing.rbc.ru
www.marketing.rbc.ru ИТ инфраструктура колледжа (для студентов)
ИТ инфраструктура колледжа (для студентов) Размеры и оборудование баскетбольной площадки
Размеры и оборудование баскетбольной площадки Рынок ценных бумаг
Рынок ценных бумаг Знаю, что горцам, Хоть нравы их строги,В облачном крае скалистых земельПесня нужна, словно лошадь В дороге,Песня н
Знаю, что горцам, Хоть нравы их строги,В облачном крае скалистых земельПесня нужна, словно лошадь В дороге,Песня н Каша - радость наша
Каша - радость наша Khudozhestvennaya_obrabotka_dereva
Khudozhestvennaya_obrabotka_dereva Введение стандартов ISO на системы менеджмента в практику российской компанииКейс в продолжение доклада «Международные ст
Введение стандартов ISO на системы менеджмента в практику российской компанииКейс в продолжение доклада «Международные ст Однофазные линейные электрические цепи синусоидального тока. Электродвижущие силы, напряжения и токи
Однофазные линейные электрические цепи синусоидального тока. Электродвижущие силы, напряжения и токи Рациональный потребительский бюджет
Рациональный потребительский бюджет Интегрированное производство шприцев III поколения с усовершенствованной иглой для внутримышечных инъекций
Интегрированное производство шприцев III поколения с усовершенствованной иглой для внутримышечных инъекций Социально-значимое проектирование в формировании метапредметных компетенций в условиях перехода к ФГОС ООО
Социально-значимое проектирование в формировании метапредметных компетенций в условиях перехода к ФГОС ООО Развитие творческого мышления на урокахинформатики.
Развитие творческого мышления на урокахинформатики. Presentation Title Here
Presentation Title Here  Основы теории графов
Основы теории графов source(3)
source(3) «1С:Подрядчик строительства 3.0. Управление строительным производством»
«1С:Подрядчик строительства 3.0. Управление строительным производством» Газгольдеры. Газгольдеры для нефтебаз
Газгольдеры. Газгольдеры для нефтебаз Особенности проведения государственной (итоговой) аттестации выпускников общеобразовательных учреждений в 2012 году
Особенности проведения государственной (итоговой) аттестации выпускников общеобразовательных учреждений в 2012 году Символические образы в романе И.А. Гончарова «Обломов»
Символические образы в романе И.А. Гончарова «Обломов» Деление
Деление  Венера в знаках Зодиака
Венера в знаках Зодиака Fairy Pairs. Площадки для рекламы
Fairy Pairs. Площадки для рекламы Автоматизация водоснабжения
Автоматизация водоснабжения Презентация на тему КВН по сказкам Пушкина
Презентация на тему КВН по сказкам Пушкина Разбор статьи 7 нестандартных решений в бизнесе
Разбор статьи 7 нестандартных решений в бизнесе