Содержание
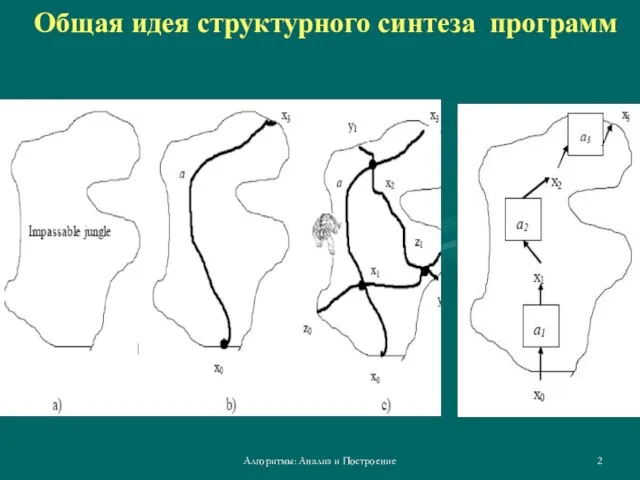
- 2. Алгоритмы: Анализ и Построение Общая идея структурного синтеза программ
- 3. Алгоритмы: Анализ и Построение Базой знаний в вычислительных моделях является множество алгоритмов, причем хороших алгоритмов (как
- 4. Алгоритмы: Анализ и Построение В дополнению к этому, так же как массив джунглей разбиваются тропинками на
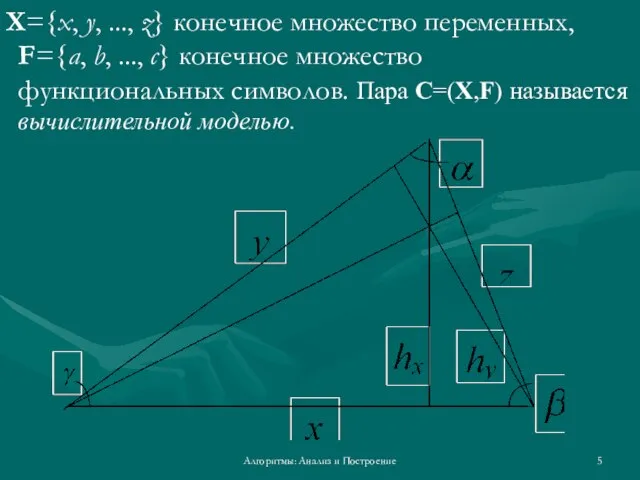
- 5. Алгоритмы: Анализ и Построение X={x, у, ..., z} конечное множество переменных, F={а, b, ..., с} конечное
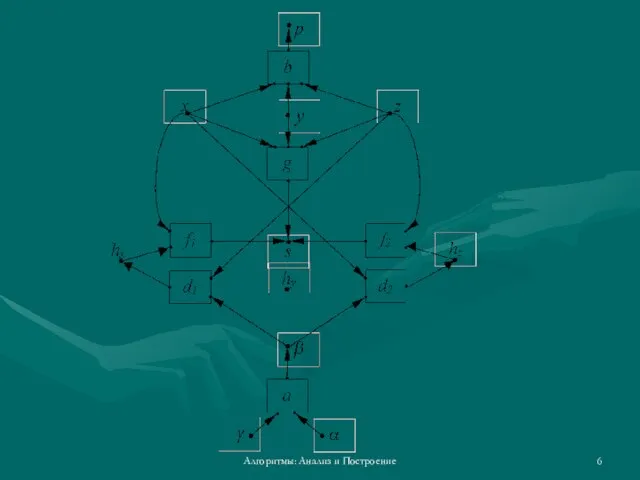
- 6. Алгоритмы: Анализ и Построение
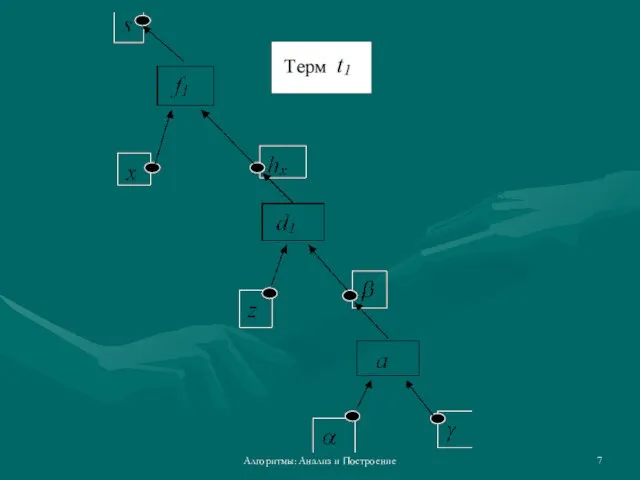
- 7. Алгоритмы: Анализ и Построение
- 8. Алгоритмы: Анализ и Построение Множества термов из T(V,F) обозначается T1, T1⊆T(V,F). Впредь будем работать только с
- 9. Алгоритмы: Анализ и Построение Планирование алгоритма Разработано много различных алгоритмов планирования. Здесь рассматривается хорошо реализуемый алгоритм,
- 10. Алгоритмы: Анализ и Построение Представление графа Пусть задана вычислительная модель С=(X,F), которая после трансляции представлена в
- 11. Алгоритмы: Анализ и Построение В восходящей части алгоритма строятся множества переменных и операций, используемых в термах
- 12. Алгоритмы: Анализ и Построение Если W⊄Vk, то планирование можно прекращать, так как в этом случае существует
- 13. Алгоритмы: Анализ и Построение Обозначим F*= Fi, и определим множества: Построение множеств Gi и Hi завершается,
- 14. Алгоритмы: Анализ и Построение Построение множеств Gi и Hi завершается, когда при некотором целом положительном r
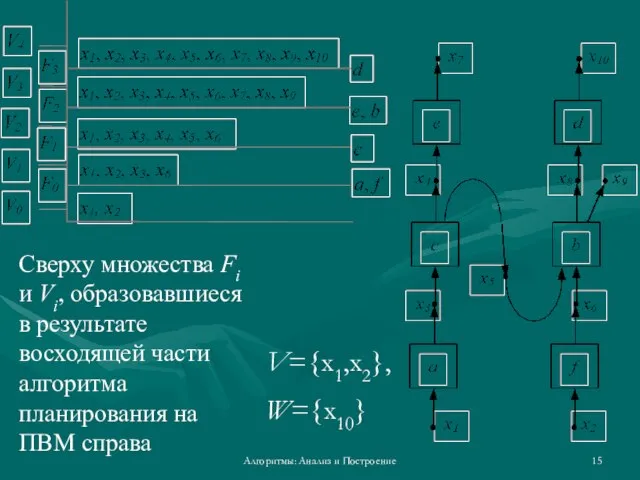
- 15. Алгоритмы: Анализ и Построение V={x1,x2}, W={x10} Сверху множества Fi и Vi, образовавшиеся в результате восходящей части
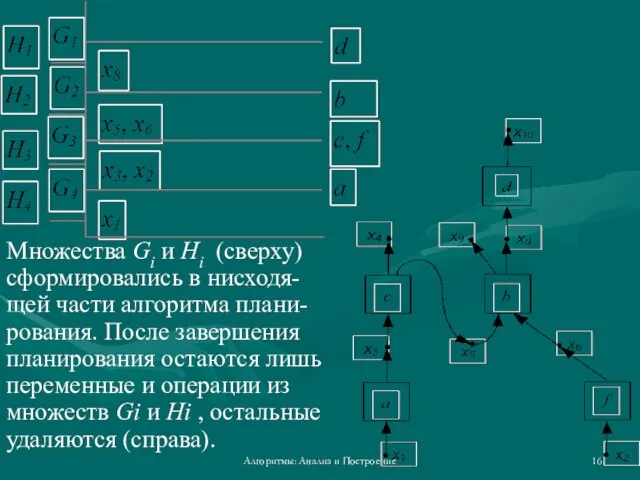
- 16. Алгоритмы: Анализ и Построение Множества Gi и Hi (сверху) сформировались в нисходя-щей части алгоритма плани-рования. После
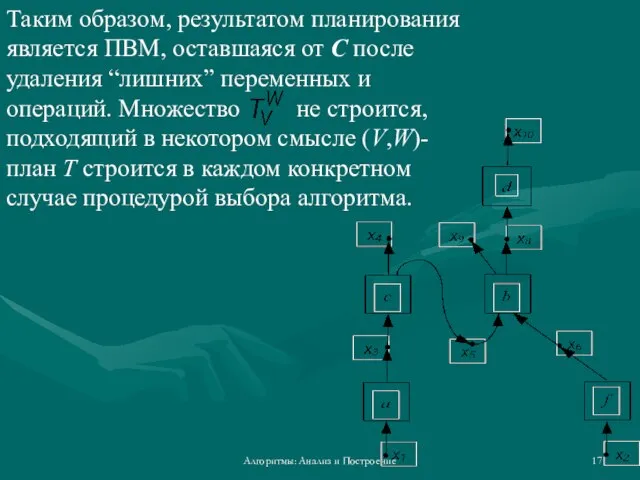
- 17. Алгоритмы: Анализ и Построение Таким образом, результатом планирования является ПВМ, оставшаяся от С после удаления “лишних”
- 18. Алгоритмы: Анализ и Построение В случае, когда W⊄Vk, сформулированная задача синтеза оказывается неразрешимой и необходимо изменить
- 19. Алгоритмы: Анализ и Построение Из описания алгоритма следует, что проверка условия in(a)⊆ Vi делается не более
- 20. Алгоритмы: Анализ и Построение При реализации алгоритма переменные и операции в ТХ и ОП могут кодироваться
- 21. Алгоритмы: Анализ и Построение ….
- 22. Алгоритмы: Анализ и Построение Ахо, Альфред, В., Хопкрофт, Джон, Ульман, Джеффри, Д. Структуры данных и алгоритмы.
- 23. Алгоритмы: Анализ и Построение Что мы называем алгоритмом? Почему? Сколько существует алгоритмов и программ, вычисляющих вычислимую
- 25. Скачать презентацию















 Методика ServQual
Методика ServQual Катя Царева представляет картины
Катя Царева представляет картины Общение и коммуникация
Общение и коммуникация PROTsEDURNYE_I_PROTsESSUAL_NYE_PRAVOOTNOShENIYa
PROTsEDURNYE_I_PROTsESSUAL_NYE_PRAVOOTNOShENIYa RAZREZY
RAZREZY Концепт-дизайн салонов маникюра LAKMODA
Концепт-дизайн салонов маникюра LAKMODA Презентация на тему Научно-практическая конференция
Презентация на тему Научно-практическая конференция Мы работаем на периметре незнания
Мы работаем на периметре незнания Об авторе Установка Ремонт камина Акции Каталог Галерея работ Отзывы Контакты
Об авторе Установка Ремонт камина Акции Каталог Галерея работ Отзывы Контакты Логистика - основные рабочие статусы
Логистика - основные рабочие статусы Презентация на тему Викторина ПДД
Презентация на тему Викторина ПДД  Создание и ведение блогов и сайтов по учебным предметам
Создание и ведение блогов и сайтов по учебным предметам ПАПКА ИНДИВИДУАЛЬНОЙ РАБОТЫ СЛУШАТЕЛЯ КУРСОВ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ УЧИТЕЛЕЙ РУССКОГО ЯЗЫКА В ШКОЛАХ С УЗБЕКСКИМ ЯЗЫКОМ ОБУЧЕН
ПАПКА ИНДИВИДУАЛЬНОЙ РАБОТЫ СЛУШАТЕЛЯ КУРСОВ ПОВЫШЕНИЯ КВАЛИФИКАЦИИ УЧИТЕЛЕЙ РУССКОГО ЯЗЫКА В ШКОЛАХ С УЗБЕКСКИМ ЯЗЫКОМ ОБУЧЕН Социальная психология практическое. Задание №8
Социальная психология практическое. Задание №8 Кадетский корпус МВД МЧС УГ №3 им. О.Г. Макарова. Проведение мероприятий, акций
Кадетский корпус МВД МЧС УГ №3 им. О.Г. Макарова. Проведение мероприятий, акций Былина как жанр. Герои былин
Былина как жанр. Герои былин Электронная почта. E-mail
Электронная почта. E-mail Осень. Магнитогорский педагогический колледж
Осень. Магнитогорский педагогический колледж Проект «мой Пушкин»
Проект «мой Пушкин» Sport in Britain
Sport in Britain Службы сопровождения в коррекционно-развивающем образовании
Службы сопровождения в коррекционно-развивающем образовании МГД-возмущениямагнитосферной плазмыУНЧ-диапазона
МГД-возмущениямагнитосферной плазмыУНЧ-диапазона Добро и зло. Понятие греха, раскаяния и воздаяния
Добро и зло. Понятие греха, раскаяния и воздаяния Презентация на тему Изделия из теста
Презентация на тему Изделия из теста Презентация на тему Игра как метод экологического воспитания
Презентация на тему Игра как метод экологического воспитания Презентация к уроку математики в 1 классе по УМК «Школа России»
Презентация к уроку математики в 1 классе по УМК «Школа России» Получение выкройки швейного изделия из журналов мод
Получение выкройки швейного изделия из журналов мод At the restaurant
At the restaurant