Методы преобразования плоскостей проекций

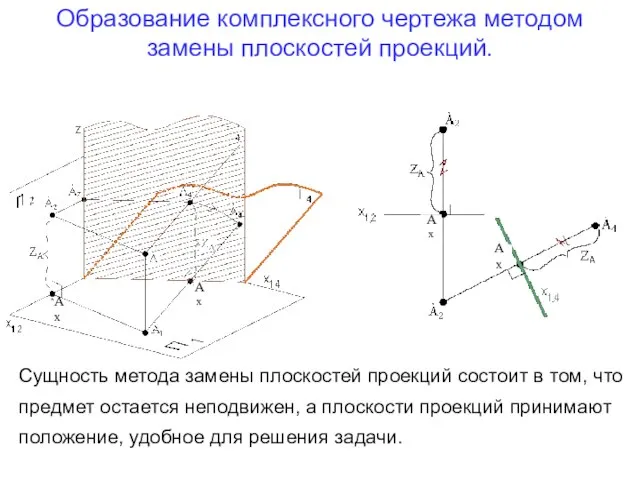
Образование комплексного чертежа методом замены плоскостей проекций.
Ах
Ах
Ах
Ах
Сущность метода замены плоскостей проекций состоит в том, что предмет остается неподвижен, а плоскости проекций принимают положение, удобное для решения задачи.

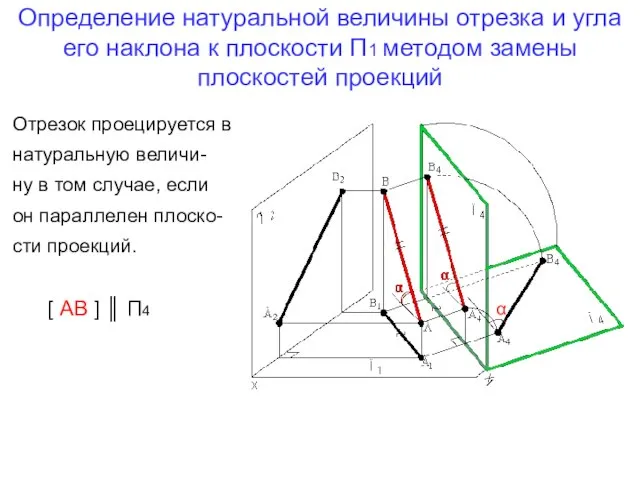
Определение натуральной величины отрезка и угла его наклона к плоскости П1 методом замены плоскостей проекций
Отрезок проецируется в натуральную величи-
ну в том случае, если
он параллелен плоско-
сти проекций.
[ АВ ] ║ П4
α

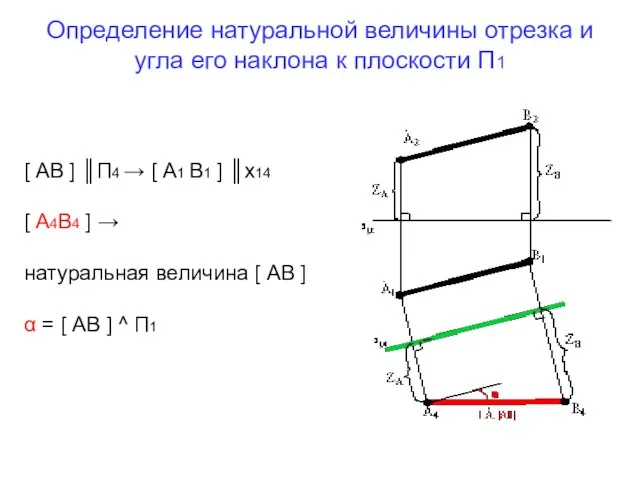
Определение натуральной величины отрезка и угла его наклона к плоскости П1
[ АВ ] ║П4 → [ А1 В1 ] ║х14
[ А4В4 ] →
натуральная величина [ АВ ]
α = [ АВ ] ^ П1

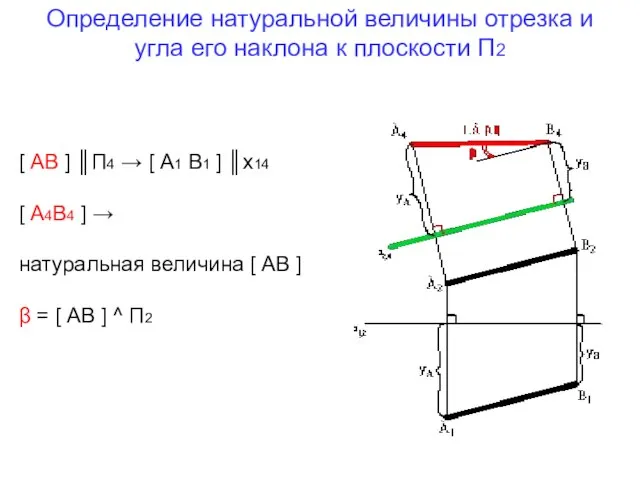
Определение натуральной величины отрезка и угла его наклона к плоскости П2
[ АВ ] ║П4 → [ А1 В1 ] ║х14
[ А4В4 ] →
натуральная величина [ АВ ]
β = [ АВ ] ^ П2

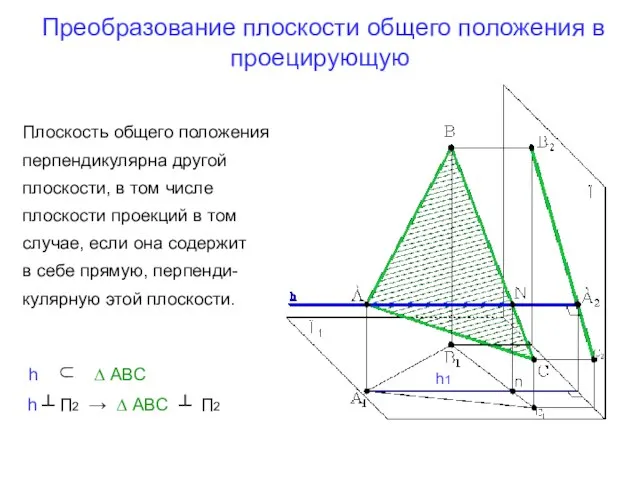
Преобразование плоскости общего положения в проецирующую
Плоскость общего положения
перпендикулярна другой
плоскости, в том числе
плоскости проекций в том
случае, если она содержит
в себе прямую, перпенди-
кулярную этой плоскости.
h
∩
∆ АВС
h ┴ П2 → ∆ АВС ┴ П2
h1

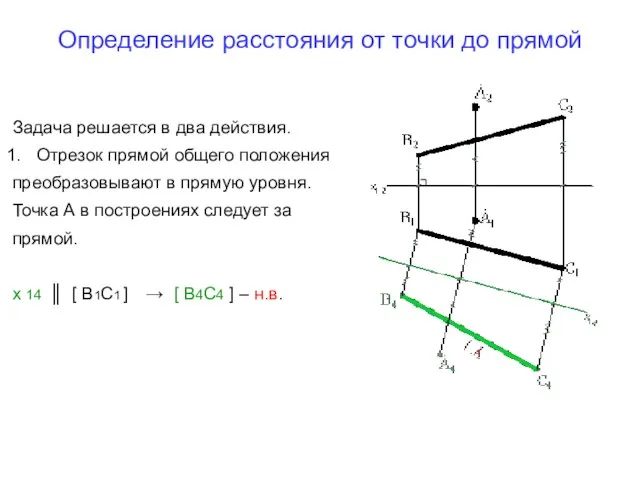
Определение расстояния от точки до прямой
Задача решается в два действия.
Отрезок прямой общего положения
преобразовывают в прямую уровня.
Точка А в построениях следует за
прямой.
х 14 ║ [ В1С1 ] → [ В4С4 ] – н.в.

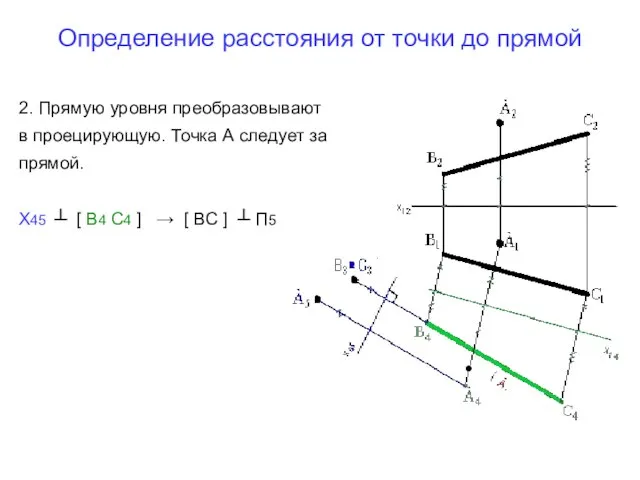
Определение расстояния от точки до прямой
2. Прямую уровня преобразовывают
в проецирующую. Точка А следует за прямой.
Х45 ┴ [ В4 С4 ] → [ ВС ] ┴ П5

Определение расстояния от точки до прямой
Отрезок прямой [ ВС ]
преобразовался в точку.
Соединяем две точки
между собой – получаем
расстояние от точки (·) А
до отрезка прямой [ ВС ].

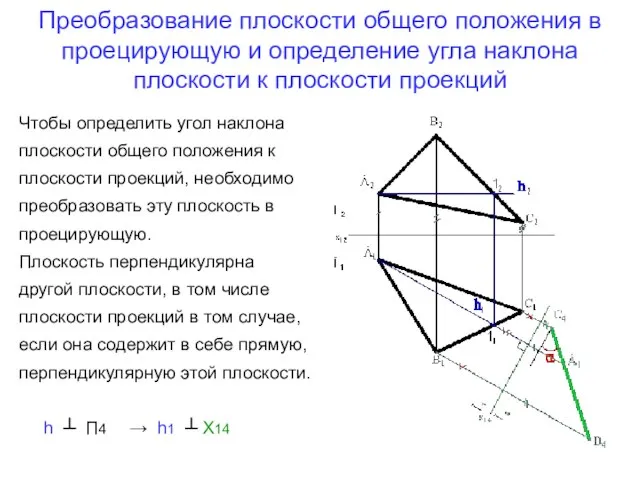
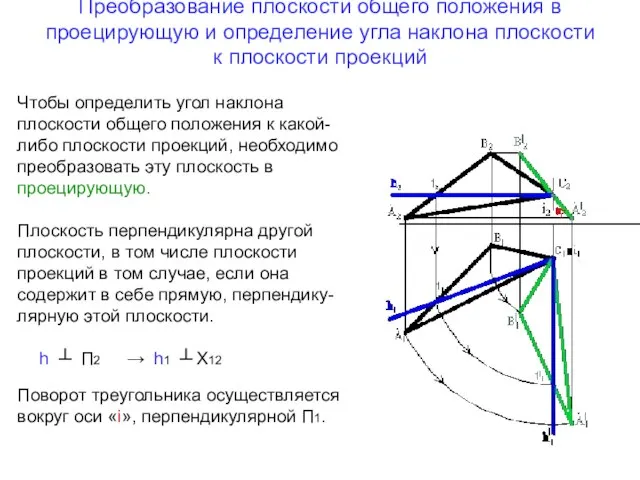
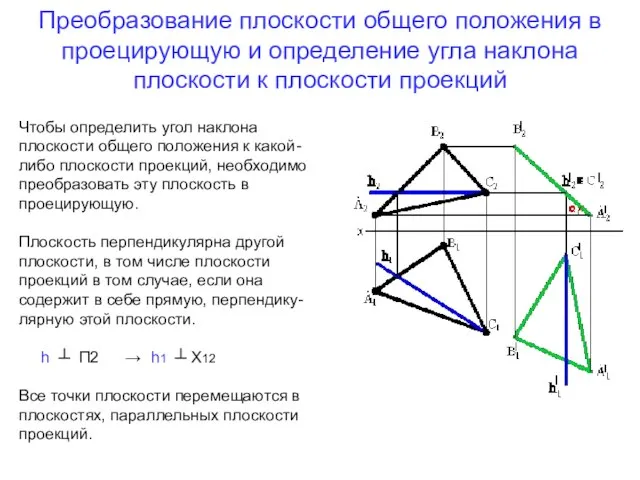
Преобразование плоскости общего положения в проецирующую и определение угла наклона плоскости к плоскости проекций
Чтобы определить угол наклона
плоскости общего положения к
плоскости проекций, необходимо
преобразовать эту плоскость в
проецирующую.
Плоскость перпендикулярна
другой плоскости, в том числе
плоскости проекций в том случае,
если она содержит в себе прямую,
перпендикулярную этой плоскости.
h ┴ П4 → h1 ┴ Х14

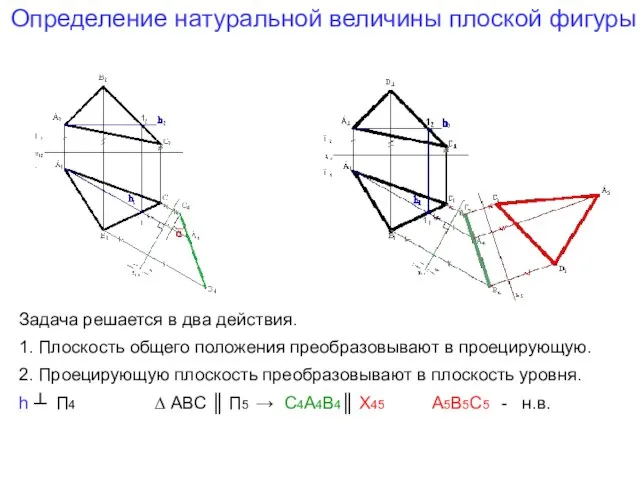
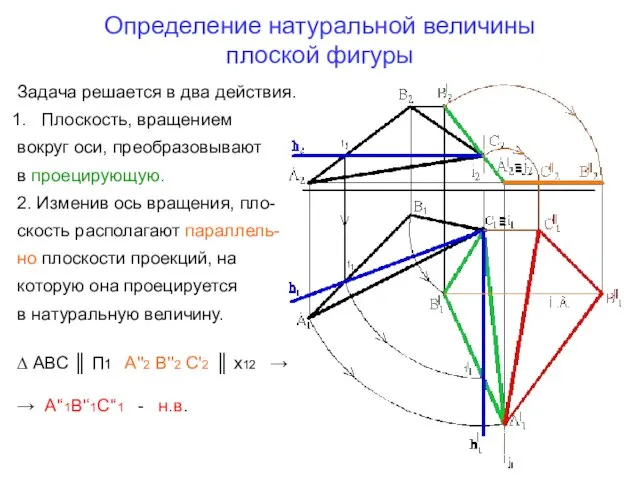
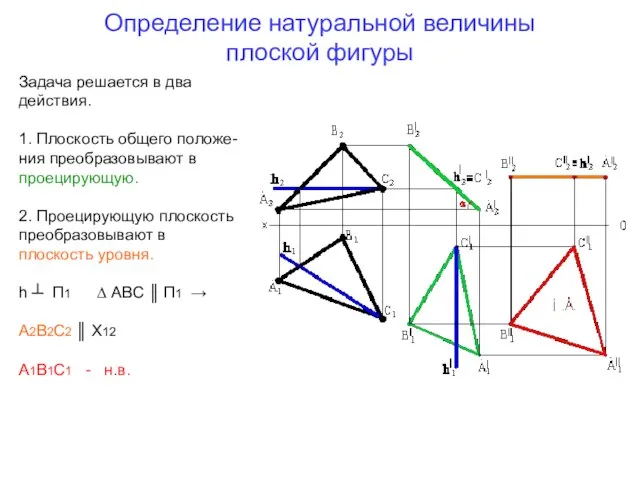
Определение натуральной величины плоской фигуры
Задача решается в два действия.
1. Плоскость общего положения преобразовывают в проецирующую.
2. Проецирующую плоскость преобразовывают в плоскость уровня.
h ┴ П4 ∆ АВС ║ П5 → С4А4В4║ Х45 А5В5С5 - н.в.

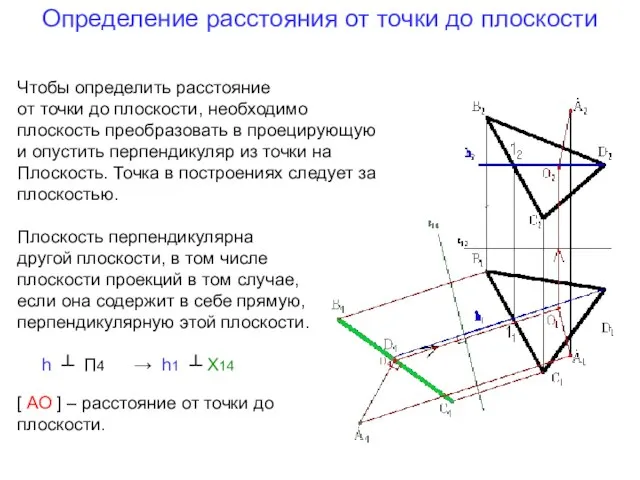
Определение расстояния от точки до плоскости
Чтобы определить расстояние
от точки до плоскости, необходимо
плоскость преобразовать в проецирующую
и опустить перпендикуляр из точки на
Плоскость. Точка в построениях следует за
плоскостью.
Плоскость перпендикулярна
другой плоскости, в том числе
плоскости проекций в том случае,
если она содержит в себе прямую,
перпендикулярную этой плоскости.
h ┴ П4 → h1 ┴ Х14
[ АО ] – расстояние от точки до
плоскости.

Определение расстояния от точки до плоскости
Рх
Рх1
Н.в.[ АО ]
Плоскость «Р» задана следами.
Чтобы определить расстояние
преобразовываем плоскость в
проецирующую, и опускаем перпендикуляр из проекции точки на след плоскости Р4.
[ АО ] – расстояние от точки до плоскости.

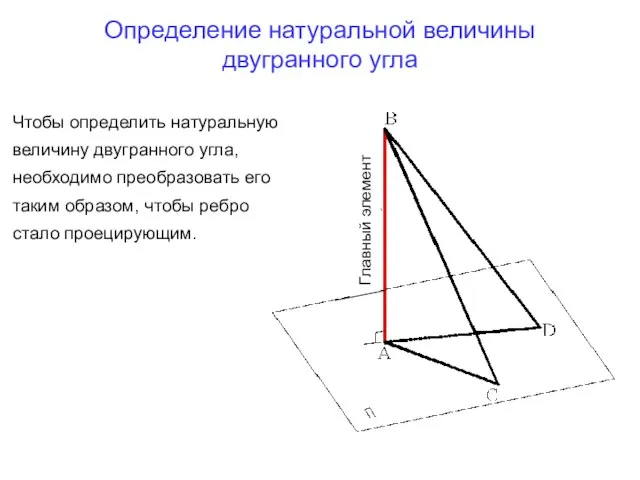
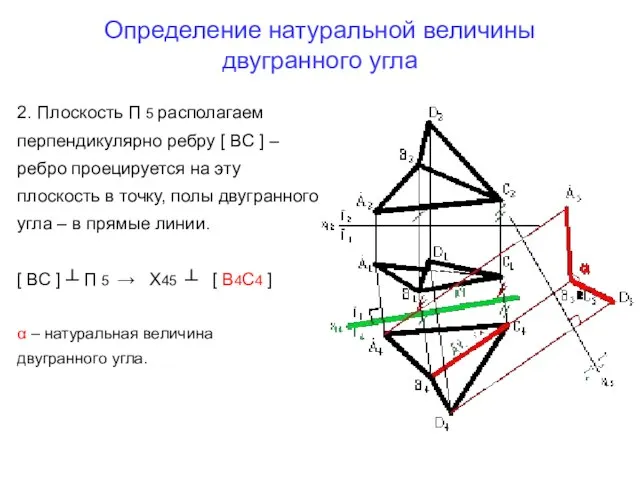
Определение натуральной величины
двугранного угла
Главный элемент
Чтобы определить натуральную
величину двугранного угла,
необходимо преобразовать его
таким образом, чтобы ребро
стало проецирующим.

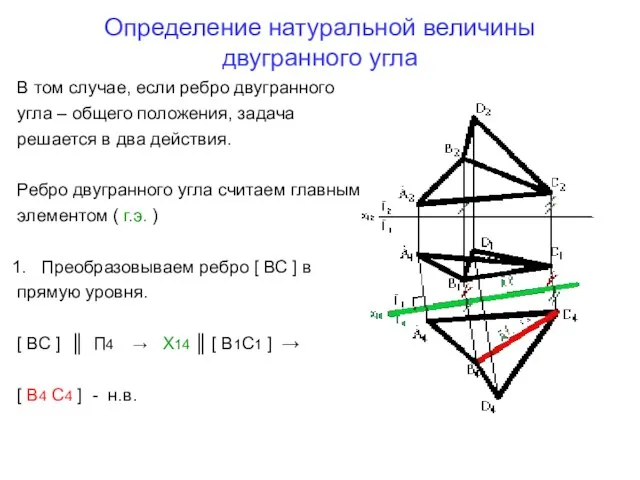
Определение натуральной величины двугранного угла
В том случае, если ребро двугранного
угла – общего положения, задача
решается в два действия.
Ребро двугранного угла считаем главным
элементом ( г.э. )
Преобразовываем ребро [ ВС ] в
прямую уровня.
[ ВС ] ║ П4 → Х14 ║ [ В1С1 ] →
[ В4 С4 ] - н.в.

Определение натуральной величины
двугранного угла
2. Плоскость П 5 располагаем
перпендикулярно ребру [ ВС ] –
ребро проецируется на эту
плоскость в точку, полы двугранного
угла – в прямые линии.
[ ВС ] ┴ П 5 → Х45 ┴ [ В4С4 ]
α – натуральная величина
двугранного угла.

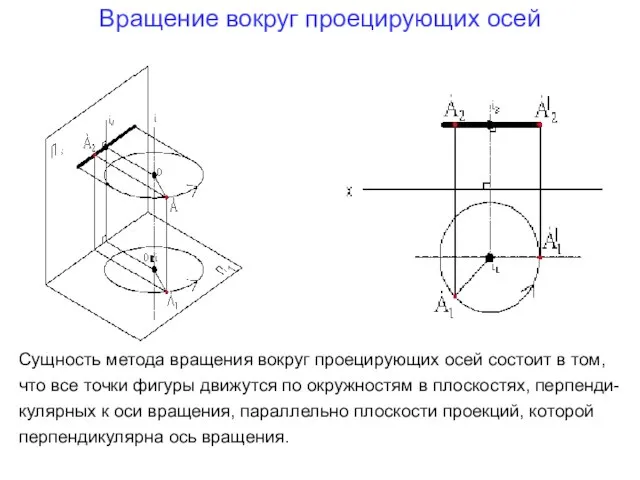
Вращение вокруг проецирующих осей
Сущность метода вращения вокруг проецирующих осей состоит в том, что все точки фигуры движутся по окружностям в плоскостях, перпенди-кулярных к оси вращения, параллельно плоскости проекций, которой перпендикулярна ось вращения.

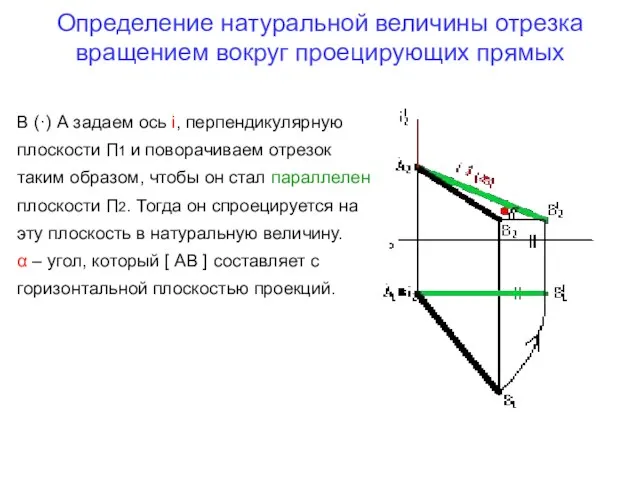
Определение натуральной величины отрезка вращением вокруг проецирующих прямых
В (·) А задаем ось i, перпендикулярную
плоскости П1 и поворачиваем отрезок
таким образом, чтобы он стал параллелен
плоскости П2. Тогда он спроецируется на
эту плоскость в натуральную величину.
α – угол, который [ АВ ] составляет с
горизонтальной плоскостью проекций.

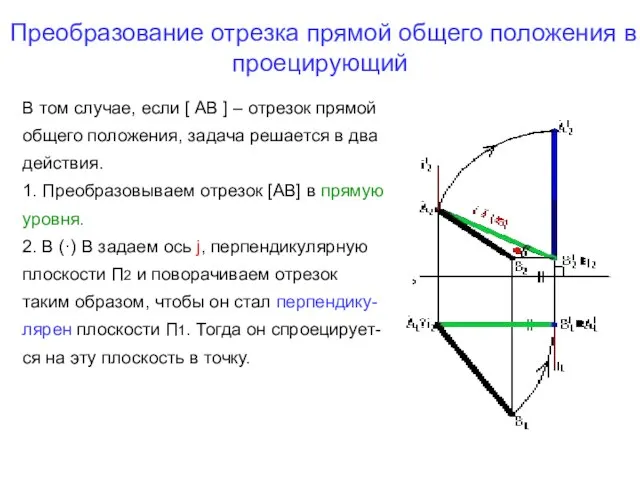
Преобразование отрезка прямой общего положения в проецирующий
В том случае, если [ АВ ] – отрезок прямой
общего положения, задача решается в два
действия.
1. Преобразовываем отрезок [АВ] в прямую уровня.
2. В (·) В задаем ось j, перпендикулярную
плоскости П2 и поворачиваем отрезок
таким образом, чтобы он стал перпендику-лярен плоскости П1. Тогда он спроецирует-ся на эту плоскость в точку.

Преобразование плоскости общего положения в проецирующую и определение угла наклона плоскости
к плоскости проекций
Чтобы определить угол наклона плоскости общего положения к какой-либо плоскости проекций, необходимо преобразовать эту плоскость в проецирующую.
Плоскость перпендикулярна другой плоскости, в том числе плоскости проекций в том случае, если она содержит в себе прямую, перпендику-лярную этой плоскости.
h ┴ П2 → h1 ┴ Х12
Поворот треугольника осуществляется вокруг оси «i», перпендикулярной П1.

Определение натуральной величины
плоской фигуры
Задача решается в два действия.
Плоскость, вращением
вокруг оси, преобразовывают
в проецирующую.
2. Изменив ось вращения, пло-
скость располагают параллель-
но плоскости проекций, на
которую она проецируется
в натуральную величину.
∆ АВС ║ П1 А''2 В''2 С'2 ║ х12 →
→ А'‘1В'‘1С'‘1 - н.в.

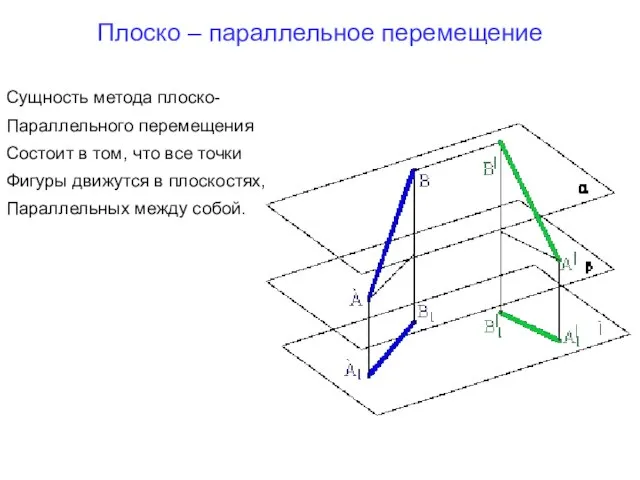
Плоско – параллельное перемещение
Сущность метода плоско-
Параллельного перемещения
Состоит в том, что все точки
Фигуры движутся в плоскостях,
Параллельных между собой.

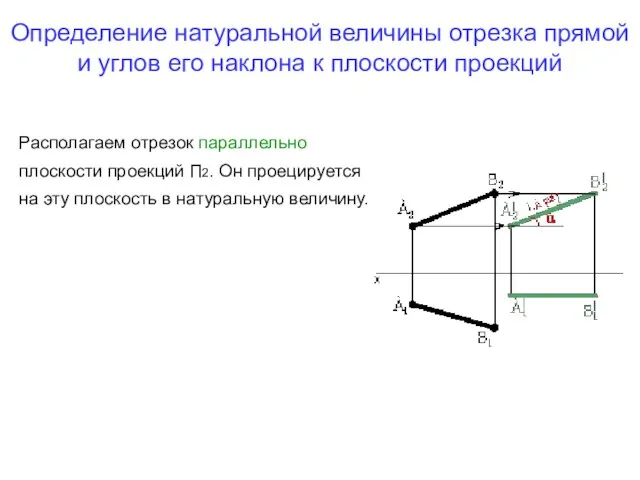
Определение натуральной величины отрезка прямой и углов его наклона к плоскости проекций
Располагаем отрезок параллельно
плоскости проекций П2. Он проецируется
на эту плоскость в натуральную величину.

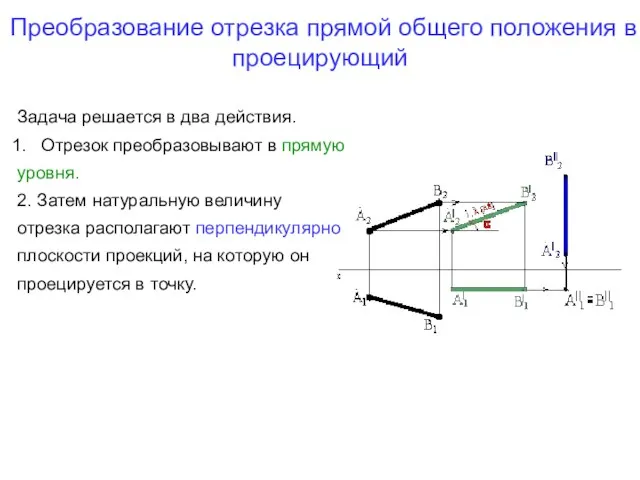
Преобразование отрезка прямой общего положения в проецирующий
Задача решается в два действия.
Отрезок преобразовывают в прямую
уровня.
2. Затем натуральную величину
отрезка располагают перпендикулярно
плоскости проекций, на которую он
проецируется в точку.

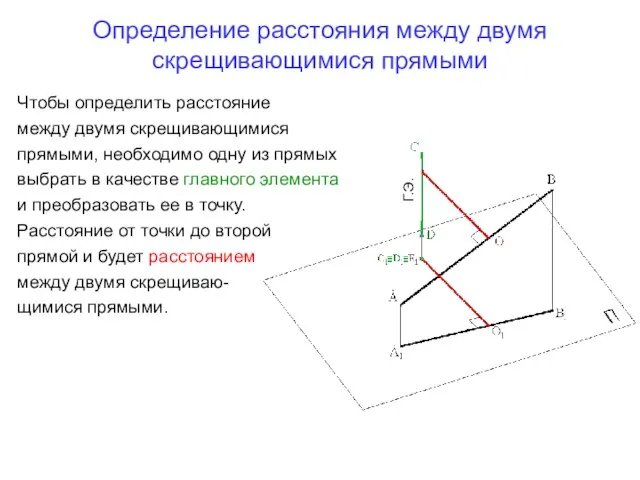
Определение расстояния между двумя скрещивающимися прямыми
Г.Э.
Чтобы определить расстояние
между двумя скрещивающимися
прямыми, необходимо одну из прямых
выбрать в качестве главного элемента
и преобразовать ее в точку.
Расстояние от точки до второй
прямой и будет расстоянием
между двумя скрещиваю-
щимися прямыми.

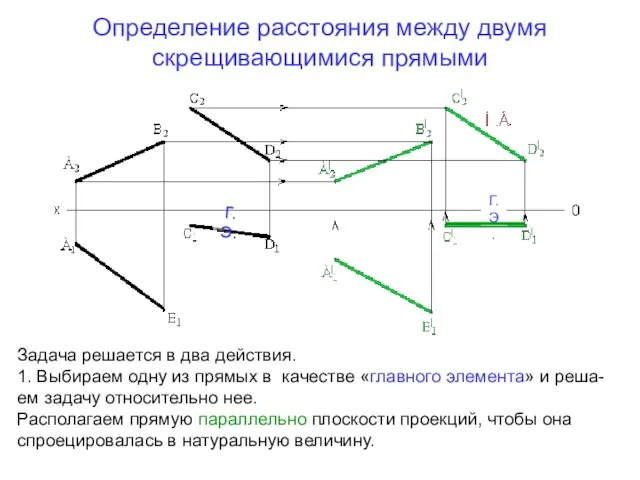
Определение расстояния между двумя скрещивающимися прямыми
Г.Э.
Г.Э.
Задача решается в два действия.
1. Выбираем одну из прямых в качестве «главного элемента» и реша-ем задачу относительно нее.
Располагаем прямую параллельно плоскости проекций, чтобы она спроецировалась в натуральную величину.

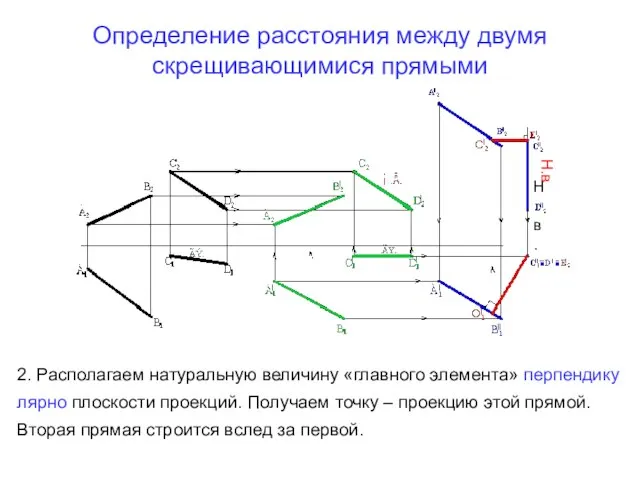
Определение расстояния между двумя скрещивающимися прямыми
Н.в.
Н.в.
2. Располагаем натуральную величину «главного элемента» перпендику
лярно плоскости проекций. Получаем точку – проекцию этой прямой.
Вторая прямая строится вслед за первой.

Преобразование плоскости общего положения в проецирующую и определение угла наклона плоскости к плоскости проекций
Чтобы определить угол наклона плоскости общего положения к какой-либо плоскости проекций, необходимо преобразовать эту плоскость в проецирующую.
Плоскость перпендикулярна другой плоскости, в том числе плоскости проекций в том случае, если она содержит в себе прямую, перпендику-лярную этой плоскости.
h ┴ П2 → h1 ┴ Х12
Все точки плоскости перемещаются в плоскостях, параллельных плоскости проекций.

Определение натуральной величины
плоской фигуры
Задача решается в два действия.
1. Плоскость общего положе-ния преобразовывают в проецирующую.
2. Проецирующую плоскость преобразовывают в плоскость уровня.
h ┴ П1 ∆ АВС ║ П1 →
А2В2С2 ║ Х12
А1В1С1 - н.в.

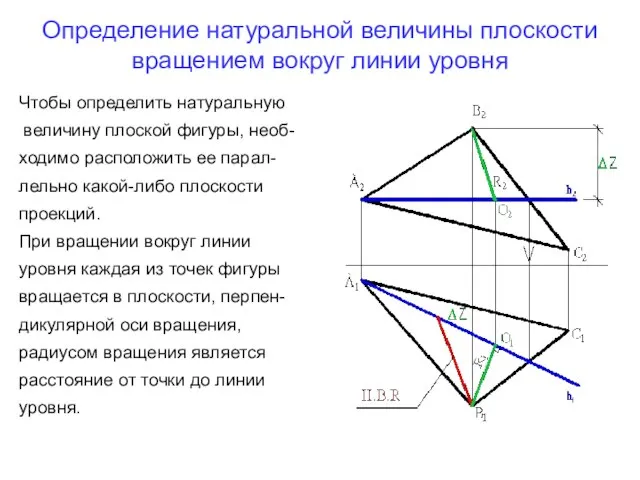
Определение натуральной величины плоскости вращением вокруг линии уровня
Чтобы определить натуральную
величину плоской фигуры, необ-
ходимо расположить ее парал-лельно какой-либо плоскости проекций.
При вращении вокруг линии уровня каждая из точек фигуры
вращается в плоскости, перпен-дикулярной оси вращения, радиусом вращения является расстояние от точки до линии уровня.