Содержание
- 2. Вопросы: Критерии оптимального выбора Математическая постановка задач планирования Геометрический метод решения задач планирования Производственная задача Транспортная
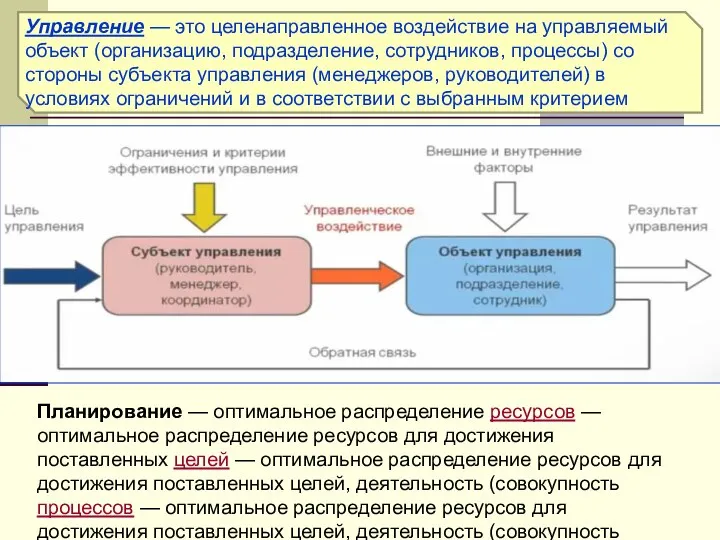
- 3. Планирование — оптимальное распределение ресурсов — оптимальное распределение ресурсов для достижения поставленных целей — оптимальное распределение
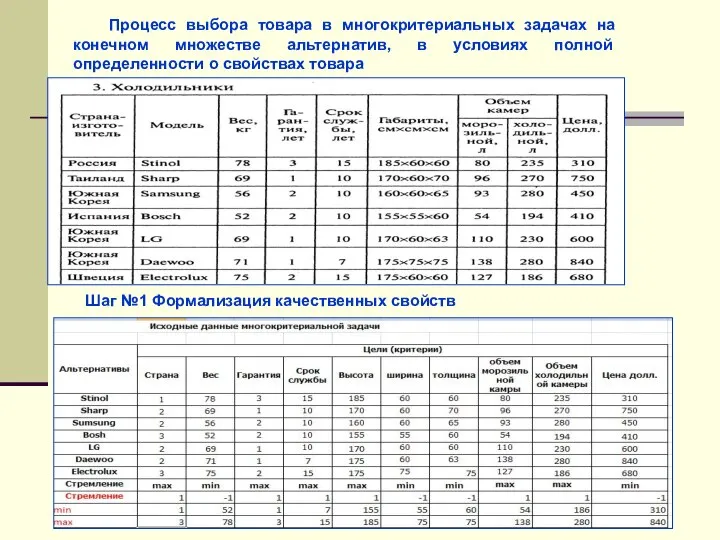
- 4. Процесс выбора товара в многокритериальных задачах на конечном множестве альтернатив, в условиях полной определенности о свойствах
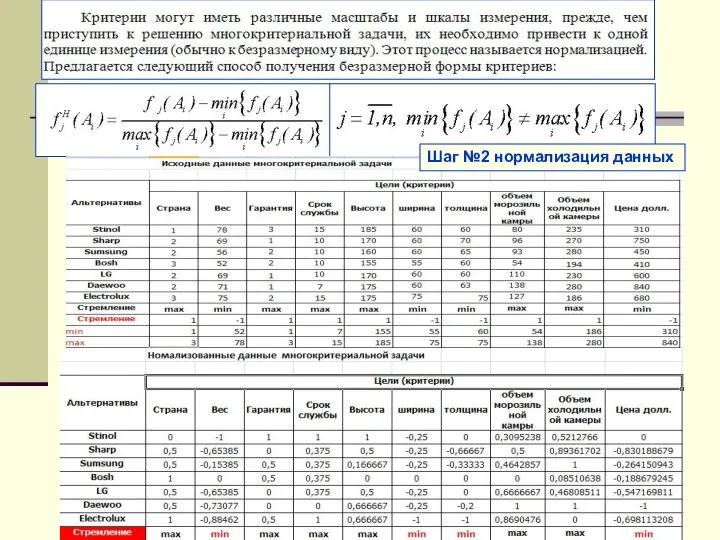
- 5. Шаг №2 нормализация данных
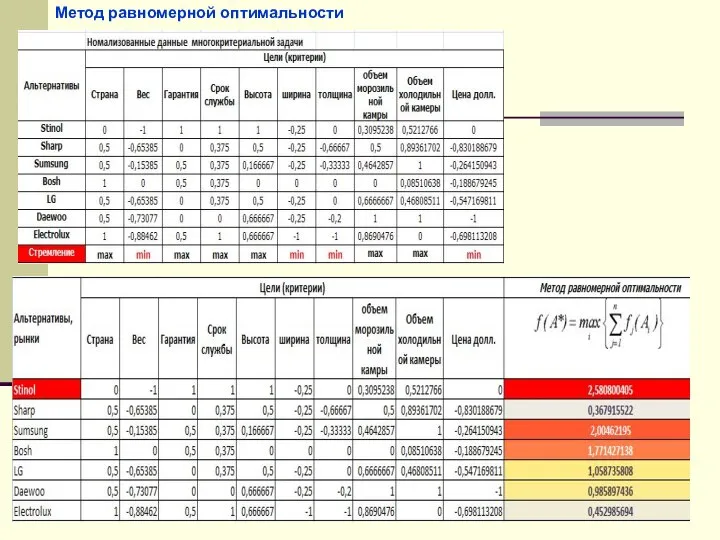
- 6. Метод равномерной оптимальности
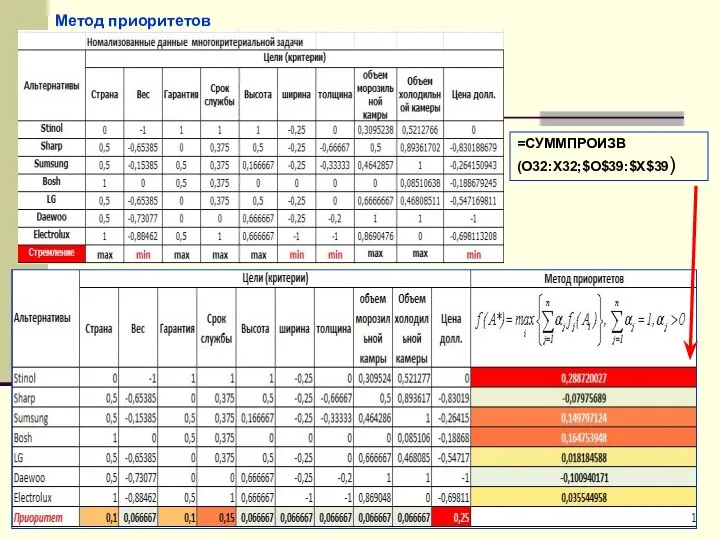
- 7. Метод приоритетов =СУММПРОИЗВ (O32:X32;$O$39:$X$39)
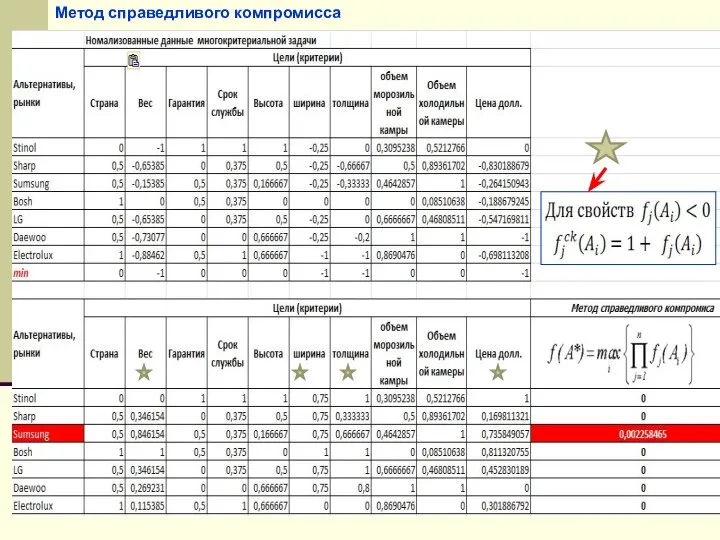
- 8. Метод справедливого компромисса
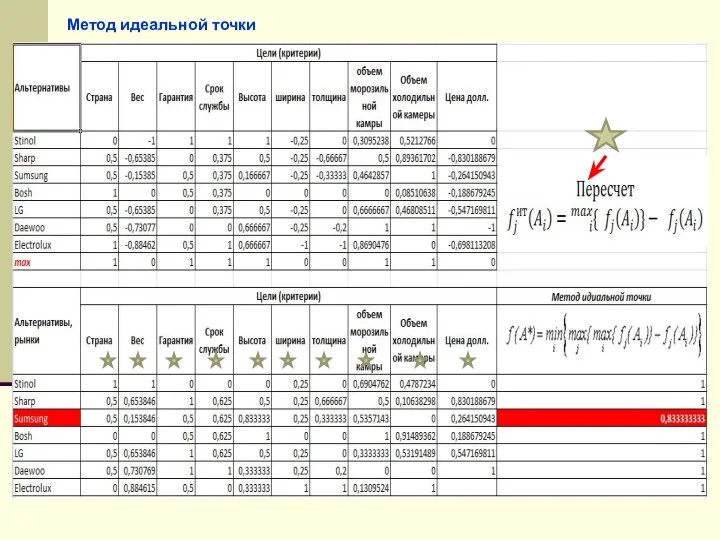
- 9. Метод идеальной точки
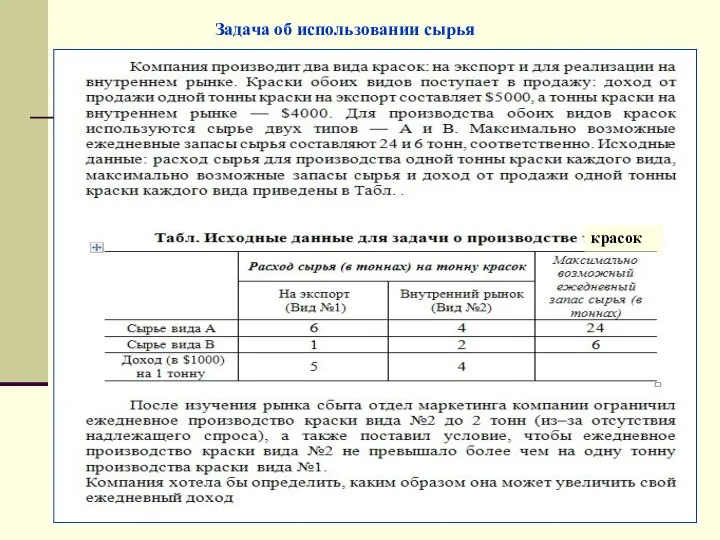
- 14. Задача об использовании сырья
- 15. Задача об использовании сырья
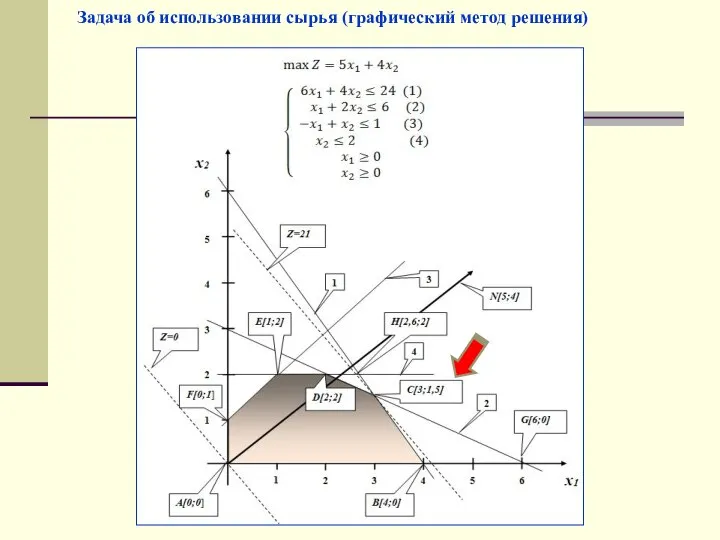
- 16. Задача об использовании сырья (графический метод решения)
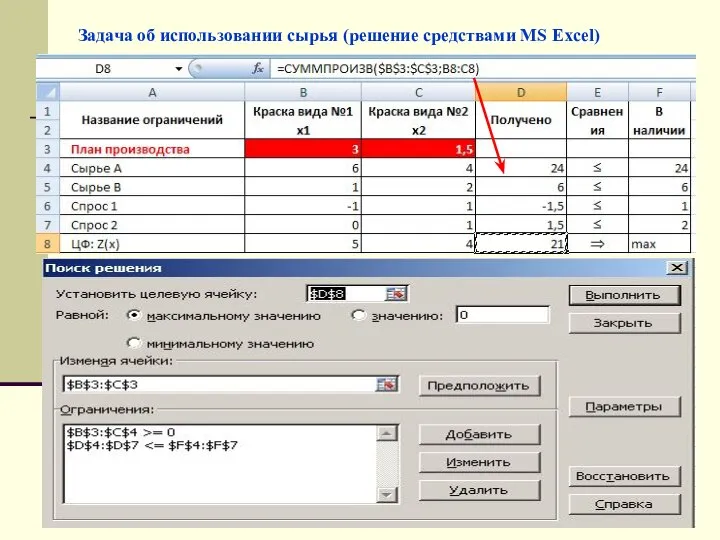
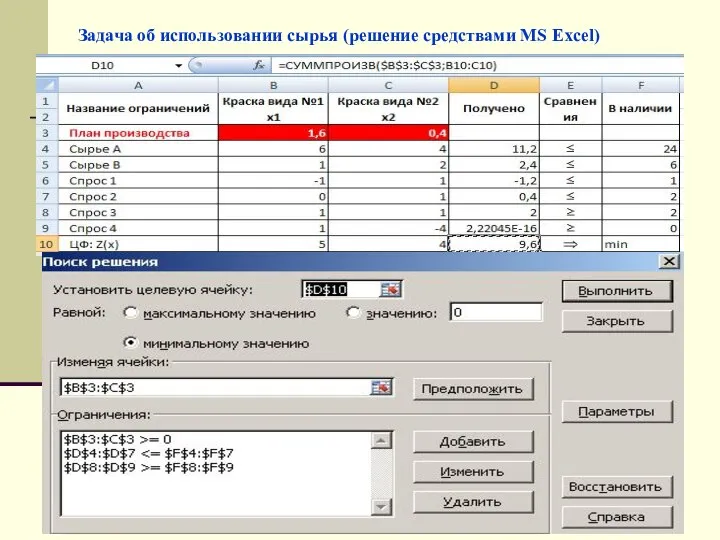
- 17. Задача об использовании сырья (решение средствами MS Excel)
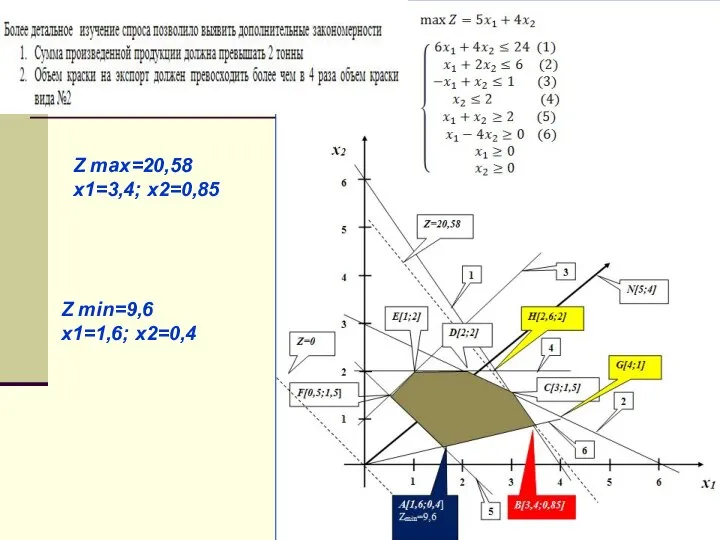
- 18. Z max=20,58 x1=3,4; x2=0,85 Z min=9,6 x1=1,6; x2=0,4
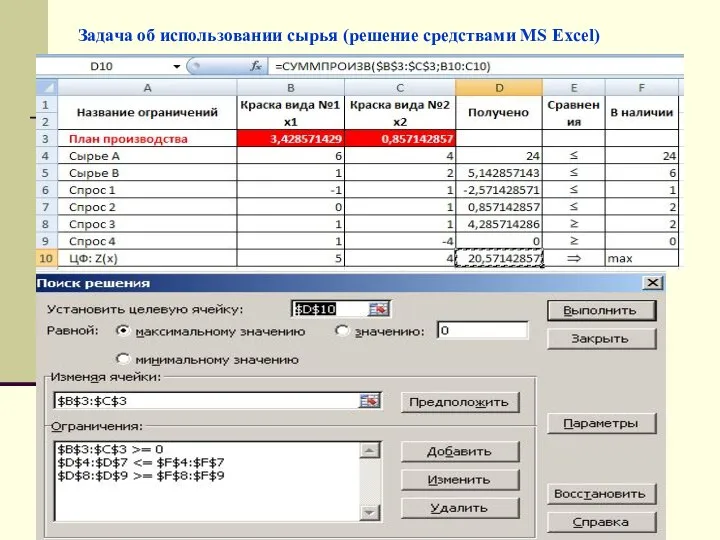
- 19. Задача об использовании сырья (решение средствами MS Excel)
- 20. Задача об использовании сырья (решение средствами MS Excel)
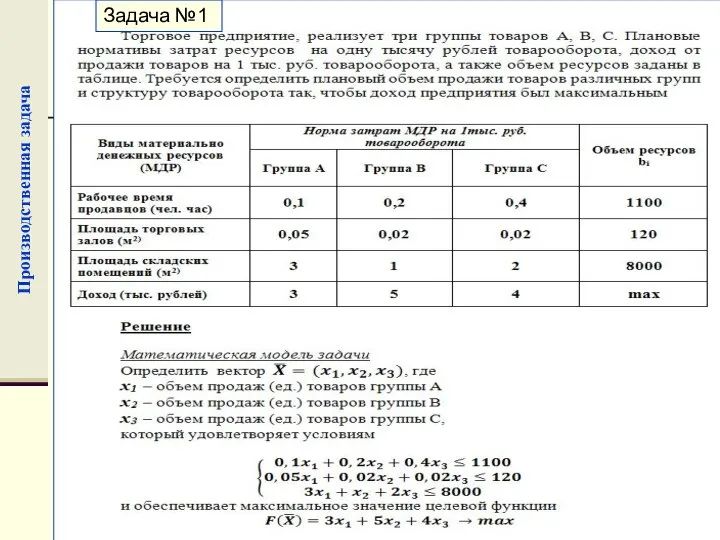
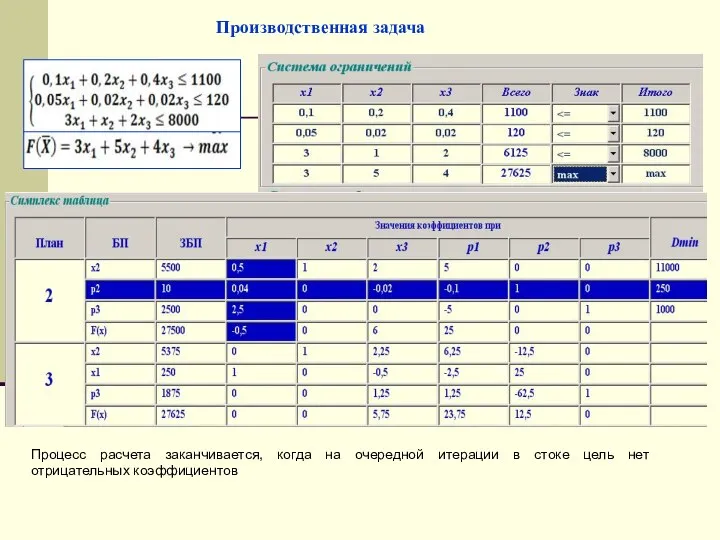
- 21. Производственная задача Задача №1
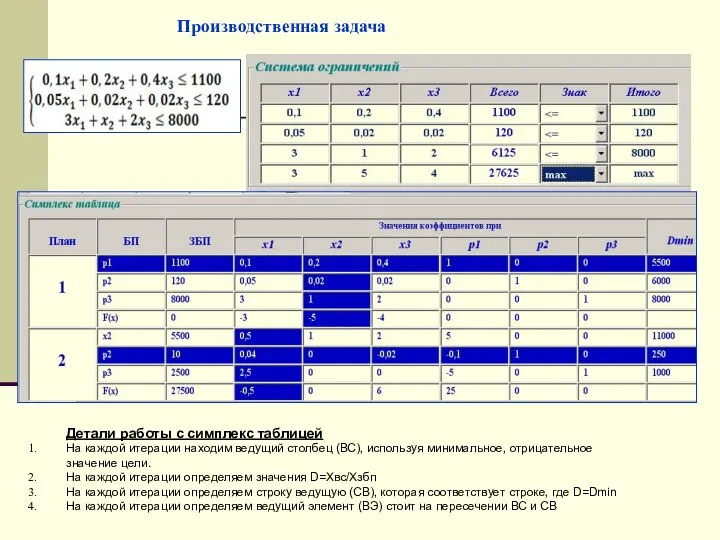
- 22. Производственная задача Детали работы с симплекс таблицей На каждой итерации находим ведущий столбец (ВС), используя минимальное,
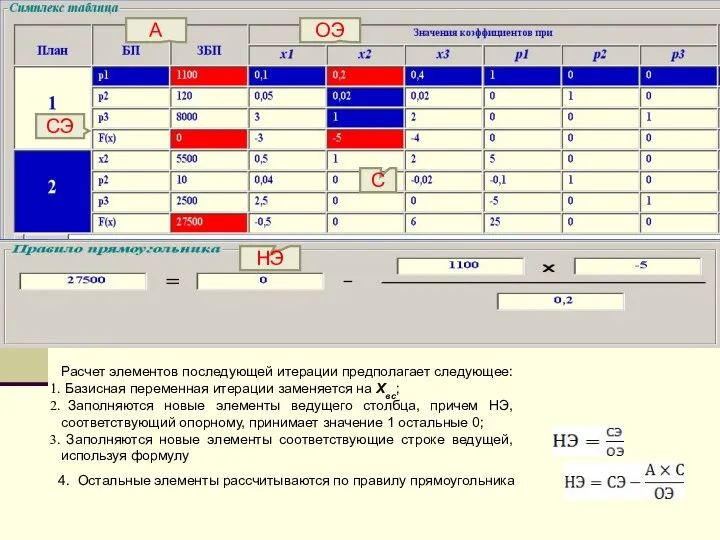
- 23. Расчет элементов последующей итерации предполагает следующее: Базисная переменная итерации заменяется на Xвс; Заполняются новые элементы ведущего
- 24. Производственная задача Процесс расчета заканчивается, когда на очередной итерации в стоке цель нет отрицательных коэффициентов
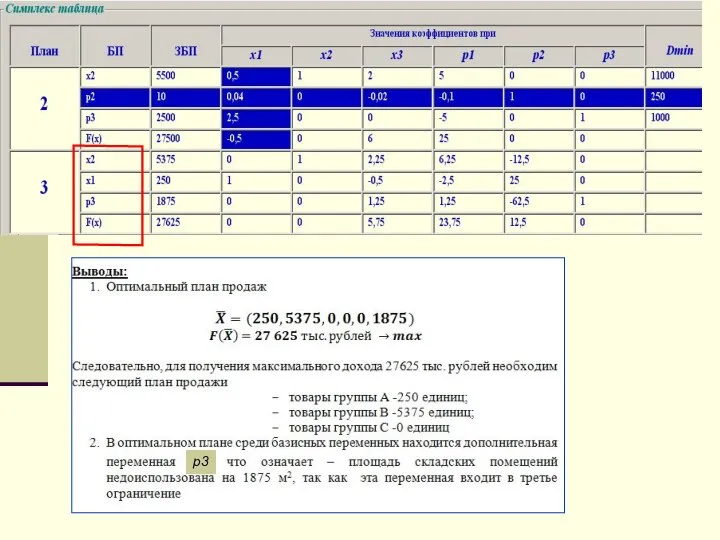
- 25. p3
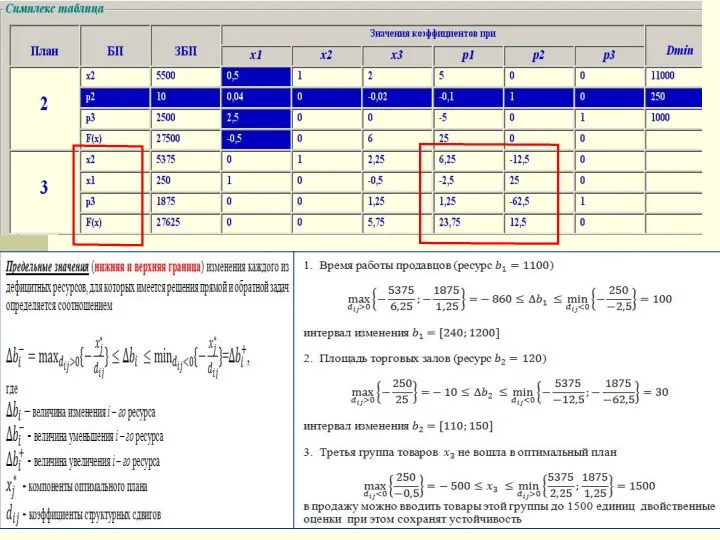
- 26. Производственная задача
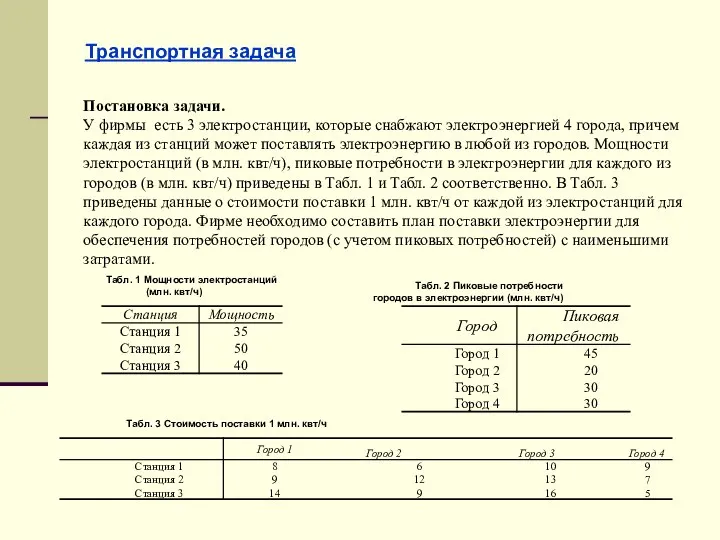
- 28. Транспортная задача
- 30. Решение транспортной задачи Решение транспортной задачи разбивается на два этапа: а) определение исходного опорного решения; б)
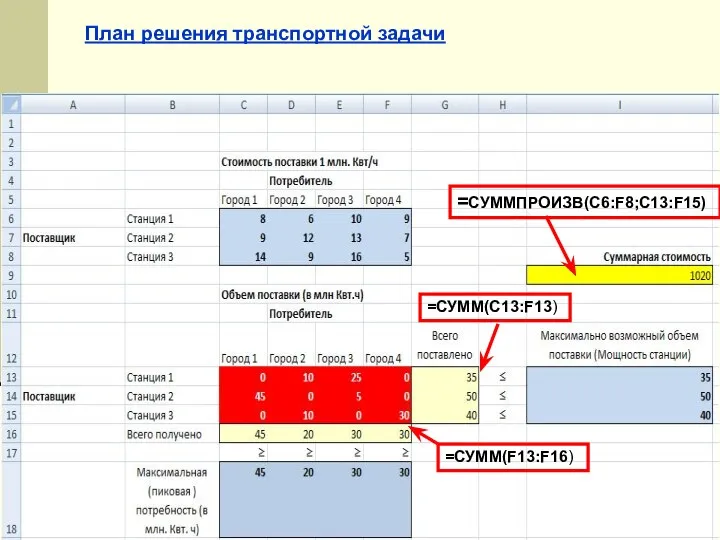
- 31. Транспортная задача Постановка задачи. У фирмы есть 3 электростанции, которые снабжают электроэнергией 4 города, причем каждая
- 32. План решения транспортной задачи =СУММПРОИЗВ(C6:F8;C13:F15) =СУММ(C13:F13) =СУММ(F13:F16)
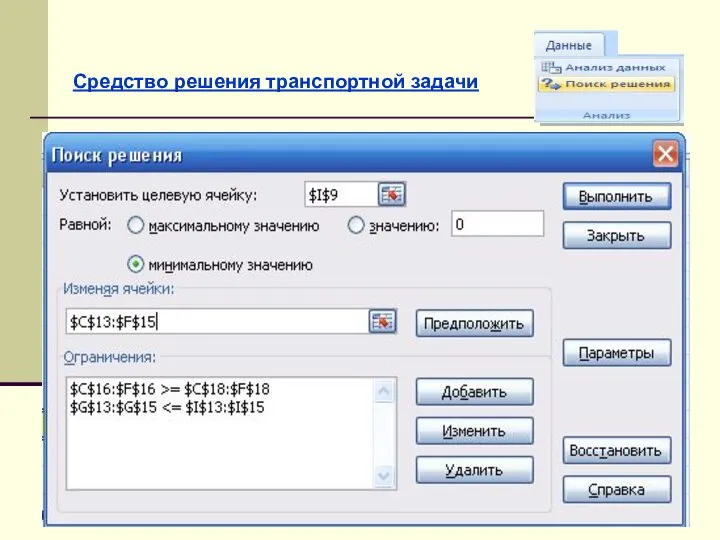
- 33. Средство решения транспортной задачи
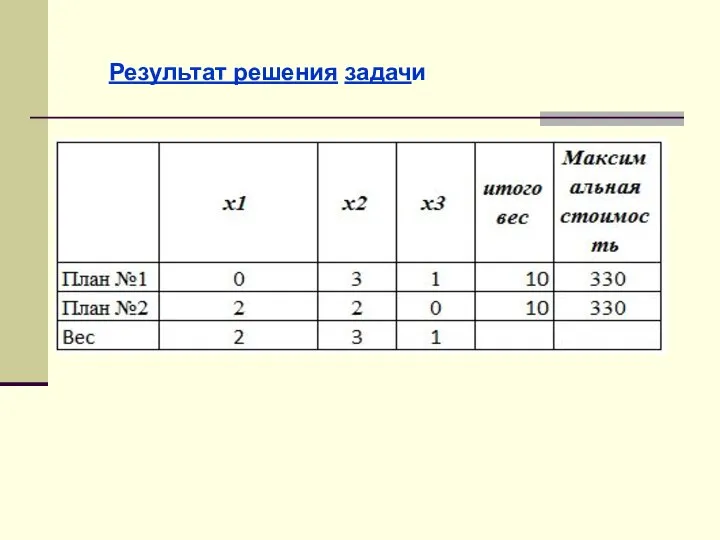
- 34. 2. Задача о рюкзаке (динамическое программирование) Постановка задачи Самолет загружается предметами N различных типов с весом
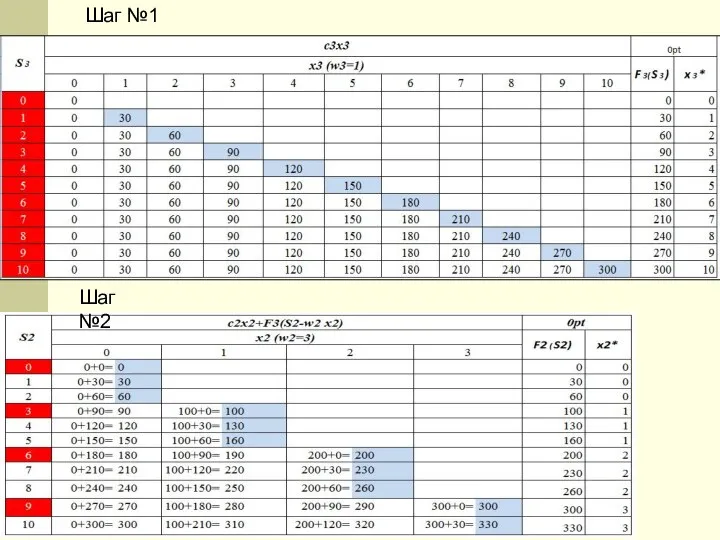
- 35. Шаг №1 Шаг №2
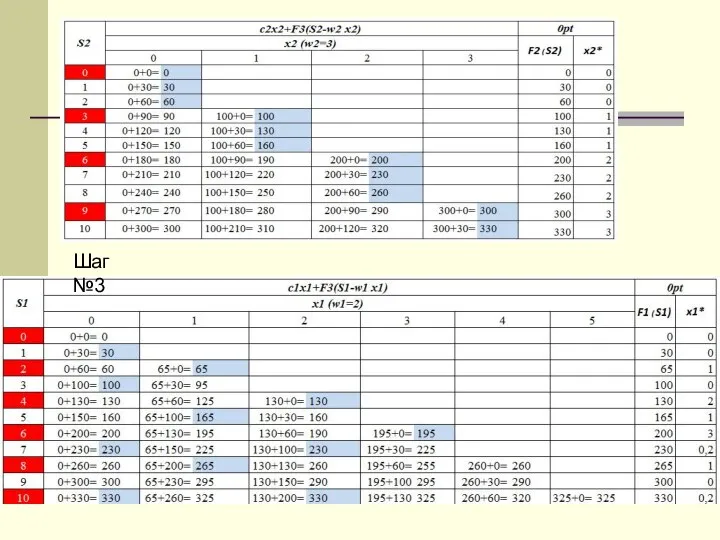
- 36. Шаг №3
- 37. Результат решения задачи
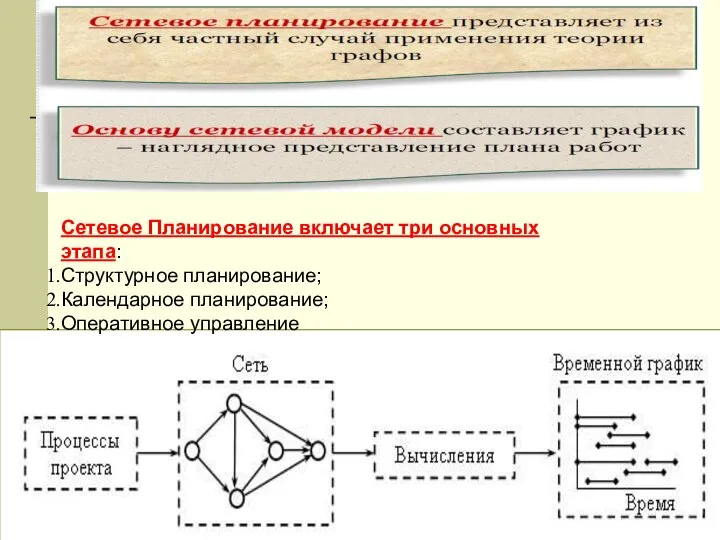
- 38. Сетевое Планирование включает три основных этапа: Структурное планирование; Календарное планирование; Оперативное управление
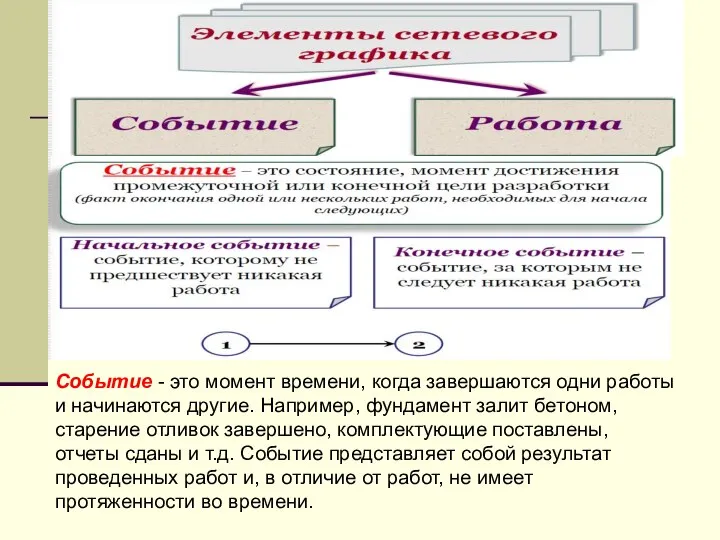
- 41. Событие - это момент времени, когда завершаются одни работы и начинаются другие. Например, фундамент залит бетоном,
- 42. По своей физической природе работы можно рассматривать как: действие: разработка чертежа, изготовление детали, заливка фундамента бетоном,
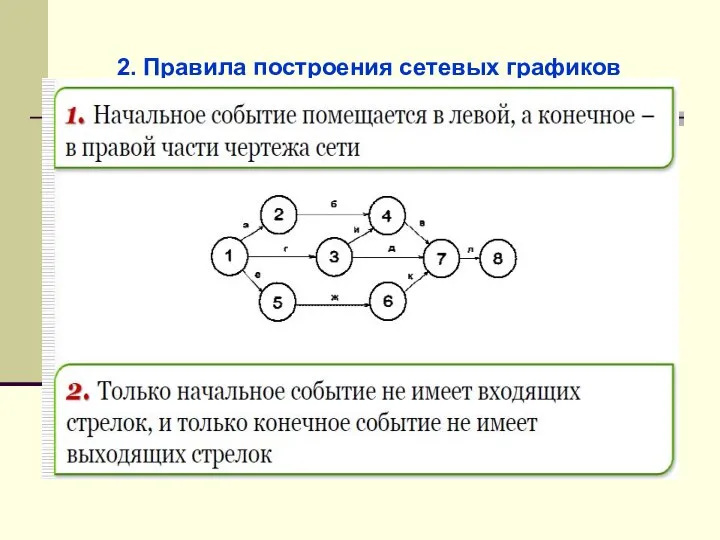
- 43. 2. Правила построения сетевых графиков
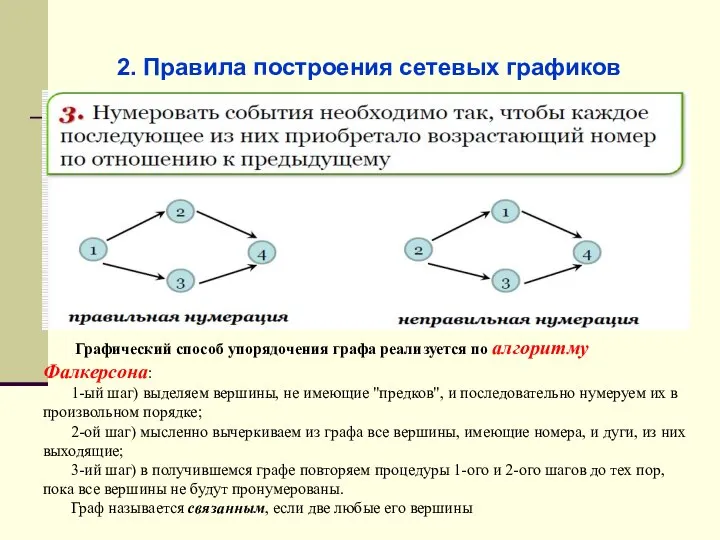
- 44. 2. Правила построения сетевых графиков Графический способ упорядочения графа реализуется по алгоритму Фалкерсона: 1-ый шаг) выделяем
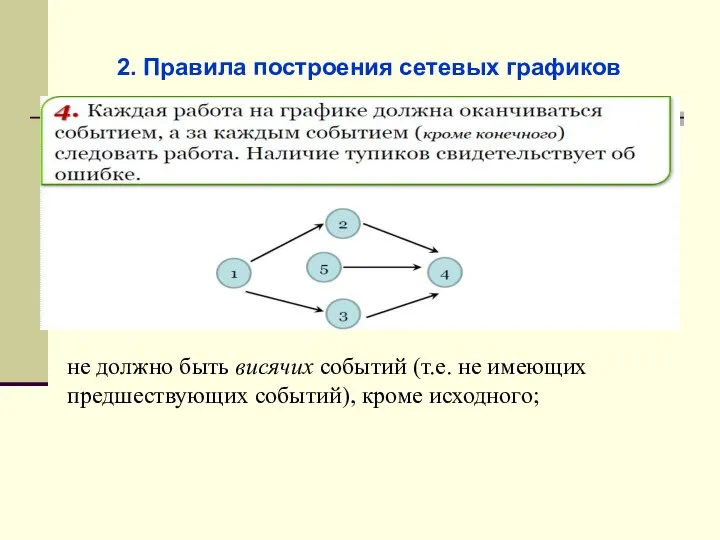
- 45. 2. Правила построения сетевых графиков не должно быть висячих событий (т.е. не имеющих предшествующих событий), кроме
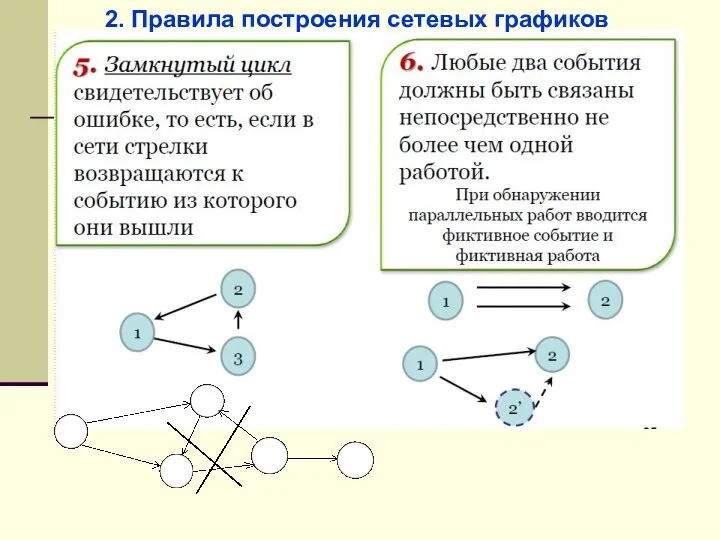
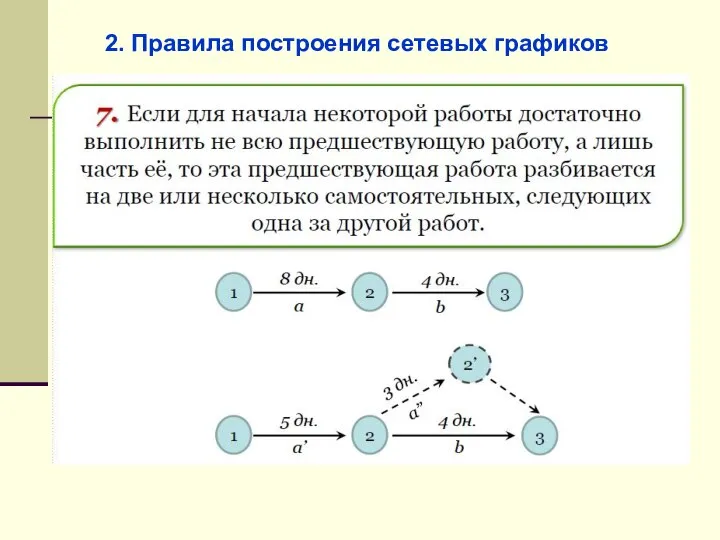
- 46. 2. Правила построения сетевых графиков
- 47. 2. Правила построения сетевых графиков
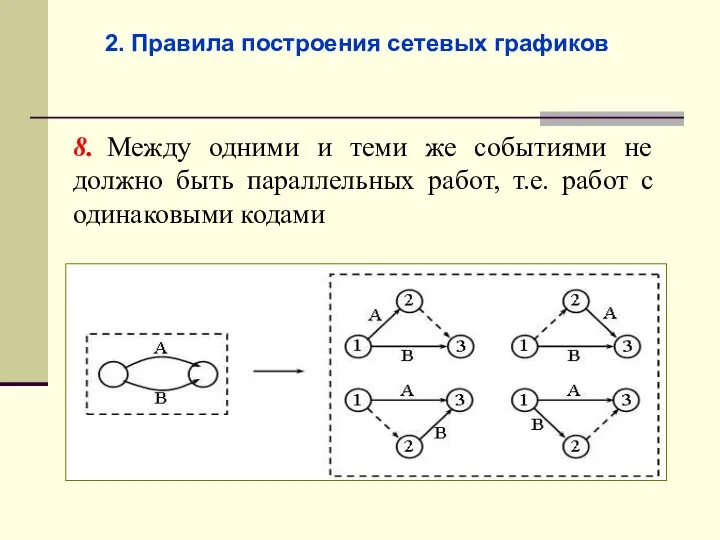
- 48. 8. Между одними и теми же событиями не должно быть параллельных работ, т.е. работ с одинаковыми
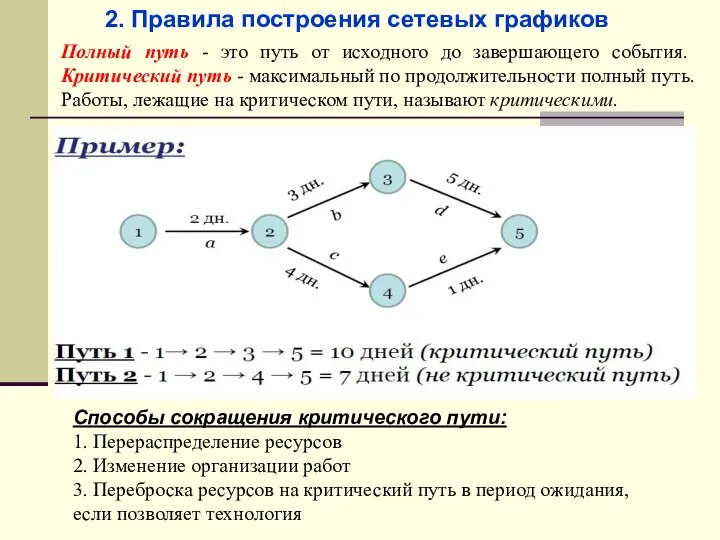
- 49. Полный путь - это путь от исходного до завершающего события. Критический путь - максимальный по продолжительности
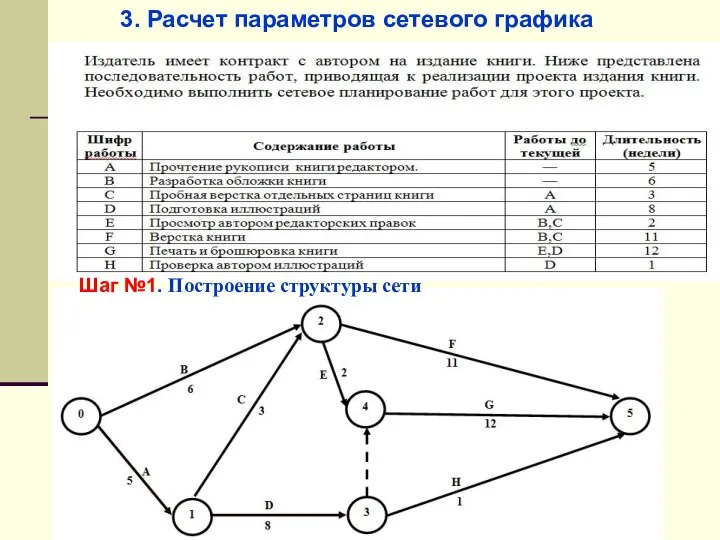
- 50. 3. Расчет параметров сетевого графика Шаг №1. Построение структуры сети
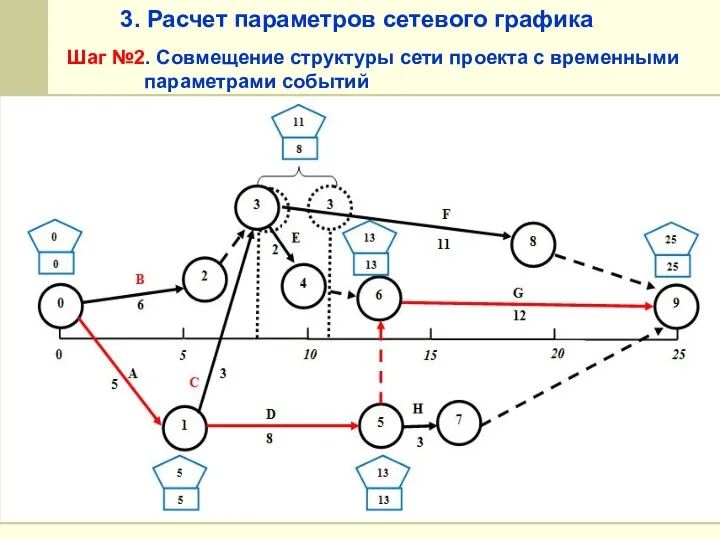
- 51. 3. Расчет параметров сетевого графика Шаг №2. Совмещение структуры сети проекта с временными параметрами событий
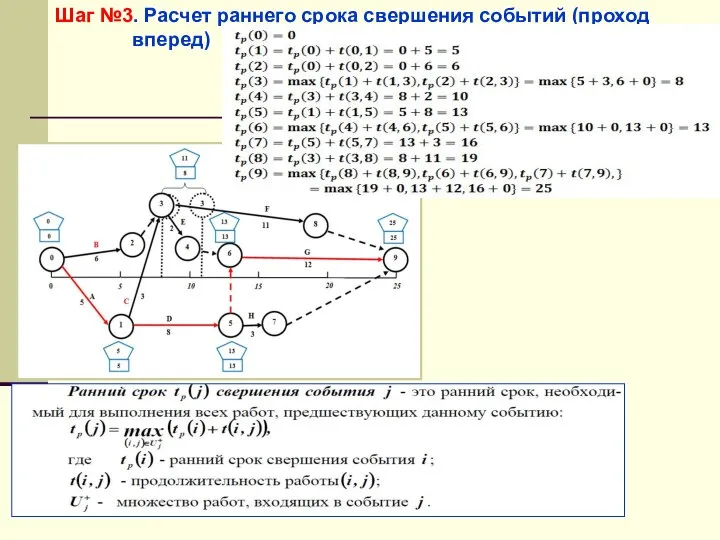
- 52. Шаг №3. Расчет раннего срока свершения событий (проход вперед)
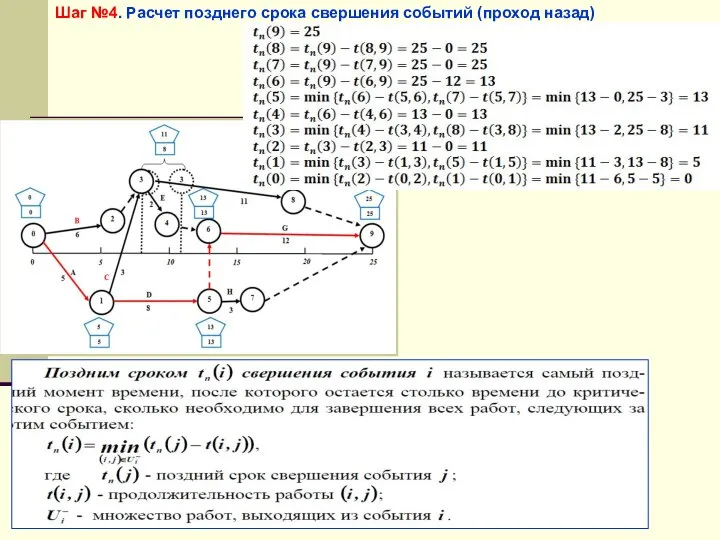
- 53. Шаг №4. Расчет позднего срока свершения событий (проход назад)
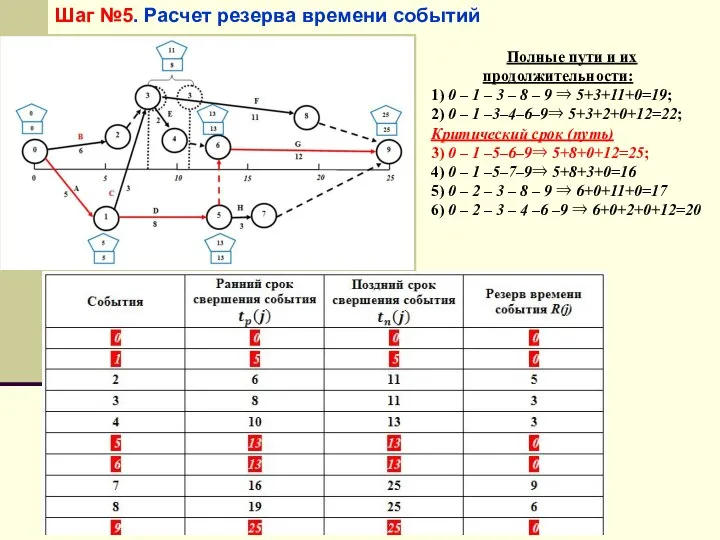
- 54. Шаг №5. Расчет резерва времени событий Полные пути и их продолжительности: 1) 0 – 1 –
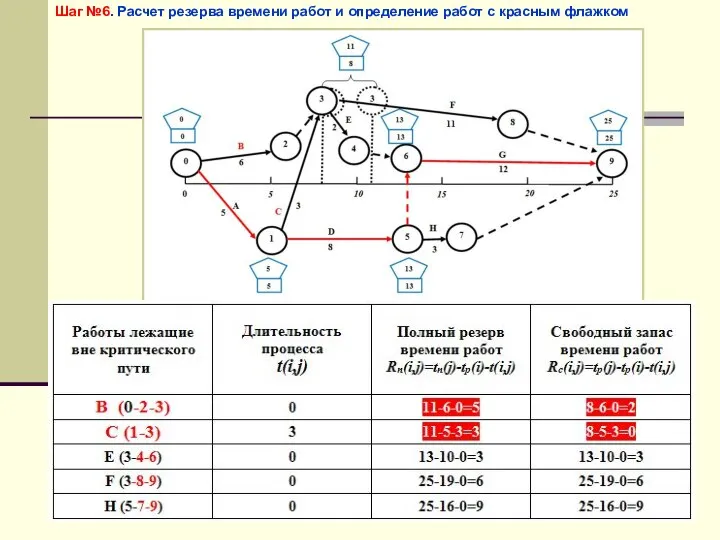
- 55. Шаг №6. Расчет резерва времени работ и определение работ с красным флажком
- 56. Шаг №6. Расчет резерва времени работ и определение работ с красным флажком
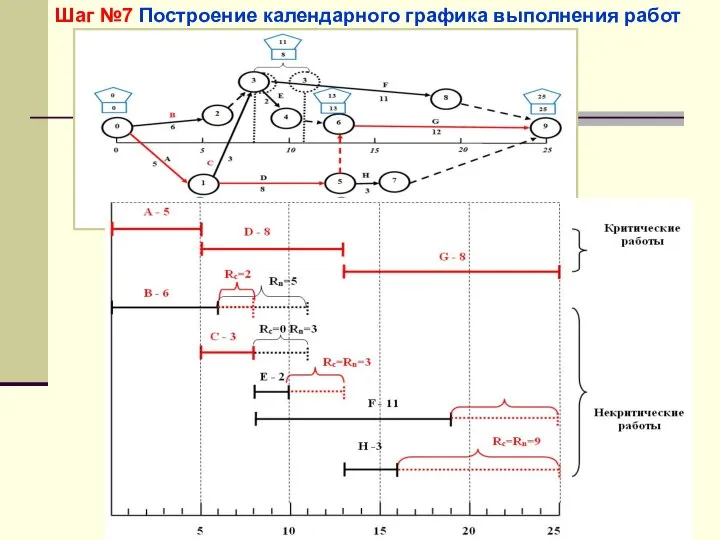
- 57. Шаг №7 Построение календарного графика выполнения работ
- 58. Расчет коэффициента нарастания затрат Cн(i,j) - стоимость выполнения работы (i,j), имеющей нормальную продолжительность Tн(i,j); Cу(i,j -
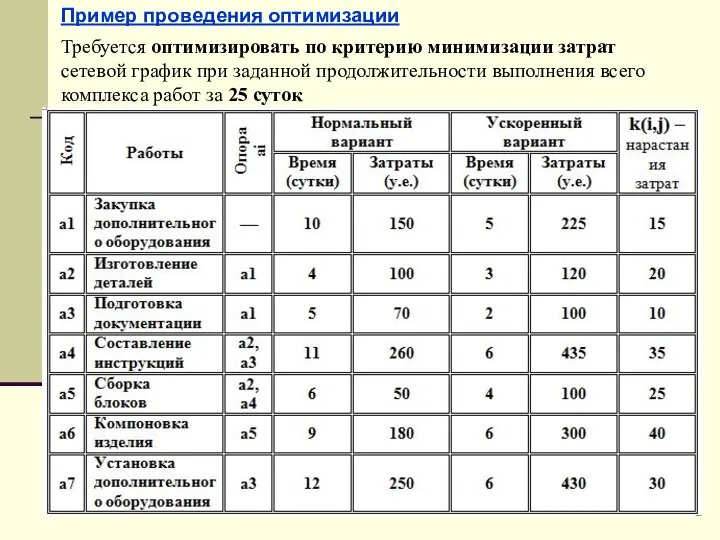
- 59. Пример проведения оптимизации Требуется оптимизировать по критерию минимизации затрат сетевой график при заданной продолжительности выполнения всего
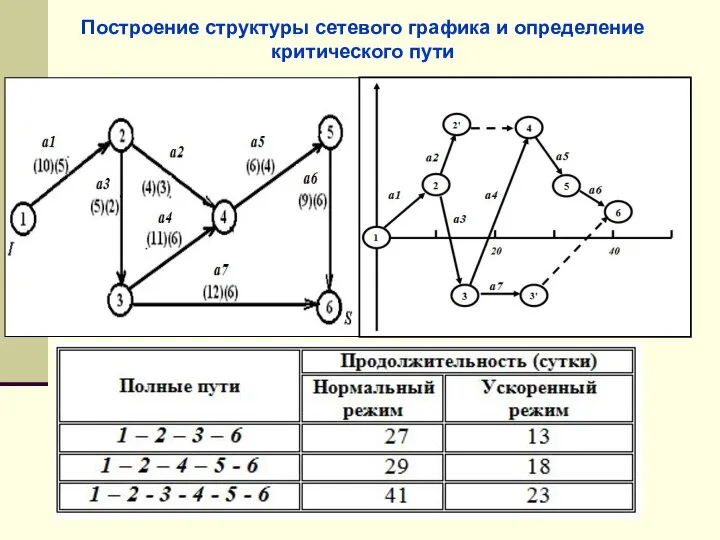
- 60. Построение структуры сетевого графика и определение критического пути
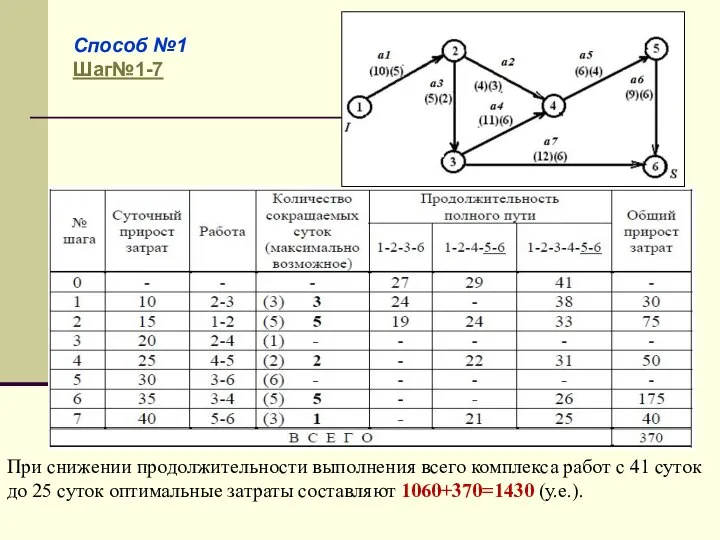
- 61. Способ №1 Шаг№1-7 При снижении продолжительности выполнения всего комплекса работ с 41 суток до 25 суток
- 63. Скачать презентацию















 Художественная культура России на рубеже 19 – 20 веков
Художественная культура России на рубеже 19 – 20 веков Поэзия Великой Отечественной войны
Поэзия Великой Отечественной войны Багатокультурність
Багатокультурність поиск новых путей:
поиск новых путей: Васильева Елена. Резюме
Васильева Елена. Резюме Dream Shop. Магазин открыток
Dream Shop. Магазин открыток Привлечение лица в качестве обвиняемого
Привлечение лица в качестве обвиняемого Воспитательная программа
Воспитательная программа «Название проекта» ФИО докладчика
«Название проекта» ФИО докладчика Система сменных модулей для грузового автотранспорта
Система сменных модулей для грузового автотранспорта Биржа
Биржа Система автоматического управления освещением зданий
Система автоматического управления освещением зданий «ЗОЛОТОЕ СЕЧЕНИЕ»
«ЗОЛОТОЕ СЕЧЕНИЕ» КАННСКИЕ ЛЬВЫ
КАННСКИЕ ЛЬВЫ УМК «Школа России»Урок русского языка по теме:«Разделительный твердый знак (ъ)»3 класс
УМК «Школа России»Урок русского языка по теме:«Разделительный твердый знак (ъ)»3 класс Фантом для занятий.
Фантом для занятий. Картинный диктант. Словарные слова на тему "Транспорт"
Картинный диктант. Словарные слова на тему "Транспорт" Подрядные работы для государственных нужд
Подрядные работы для государственных нужд ПОВОД ВЫБРАТЬ ЛУЧШЕЕ
ПОВОД ВЫБРАТЬ ЛУЧШЕЕ Правоспособность колонов
Правоспособность колонов Химическая организация клетки
Химическая организация клетки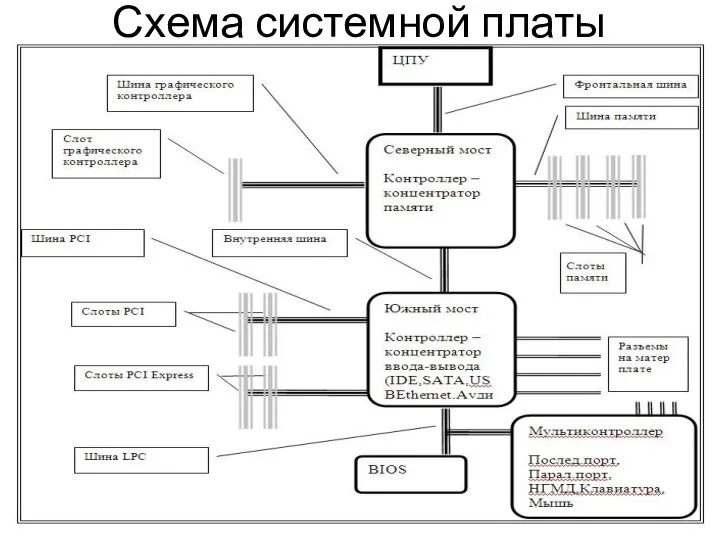 Схема системной платы
Схема системной платы roditelskoe_sobranie_27_sentyabrya_2022
roditelskoe_sobranie_27_sentyabrya_2022 Иуда Искариот Андреев
Иуда Искариот Андреев Английский, польский
Английский, польский цифровые коммуникации
цифровые коммуникации Сельское хозяйство Краснодарского края.Агропромышленный комплекс
Сельское хозяйство Краснодарского края.Агропромышленный комплекс Правовая лексика
Правовая лексика