Методы разработки алгоритмов

Метод грубой силы
©Павловская Т.А. (СПб НИУ ИТМО)

Метод грубой силы («в лоб»)
Прямой подход к решению задачи, обычно основанный непосредственно на формулировке задачи и определениях используемых ею концепций
Пример: вычисление степени числа умножением 1 на это число n раз
Применим практически для любых типов задач
Часто оказывается наиболее простым в применении
Редко дает красивые и эффективные алгоритмы
Стоимость разработки более эффективного алгоритма может оказаться неприемлемой, если требуется решить только несколько экземпляров задачи
Может оказаться полезным для решения небольших по размеру экземпляров задачи.
Может служить мерилом для определения эффективности других алгоритмов
©Павловская Т.А. (СПб НИУ ИТМО)

Пример: сортировки выбором и пузырьком
©Павловская Т.А. (СПб НИУ ИТМО)
28
16
0
29
3
-4
56
-5

Исчерпывающий перебор
Исчерпывающий перебор - подход к комбинаторным задачам с позиции грубой силы. Он предполагает:
генерацию всех возможных элементов из области определения задачи
выбор тех из них, которые удовлетворяют ограничениям, накладываемым условием задачи
поиск нужного элемента (например, оптимизирующего значение целевой функции задачи).
Примеры:
Задача коммивояжера: найти кратчайший путь по заданным N городам, чтобы каждый город посещался только один раз и конечным пунктом оказался исходный.
Задача о рюкзаке: дано N предметов заданного веса и стоимости рюкзак, выдерживающий вес W. Загрузить рюкзак с максимальной стоимостью.
Это - NP-сложные задачи (не известен алгоритм, решающий их за полиномиальное время).
©Павловская Т.А. (СПб НИУ ИТМО)
Получить все возможные маршруты, генерируя все перестановки n — 1 промежуточных городов, вычисляя длину соответствующих путей и находя кратчайший из них.
Рассмотреть все подмножества данного множества из n предметов, вычислить общий вес каждого из них для выяснения допустимости, выбрать из допустимых подмножества с максимальным весом.

Метод декомпозиции
©Павловская Т.А. (СПб НИУ ИТМО)

Метод декомпозиции
Он же - метод «разделяй и властвуй»:
Экземпляр задачи разбивается на несколько меньших экземпляров той же задачи, в идеале — одинакового размера.
Решаются меньшие экземпляры задачи (обычно рекурсивно, хотя иногда для небольших экземпляров применяется какой-нибудь другой алгоритм).
При необходимости решение исходной задачи находится путем комбинации решений меньших экземпляров.
Метод декомпозиции идеально подходит для параллельных вычислений.
©Павловская Т.А. (СПб НИУ ИТМО)

Рекуррентное уравнение декомпозиции
В общем случае экземпляр задачи размера n может быть разделен на несколько экземпляров размером n/b, а из которых требуется решить.
Обобщенное рекуррентное уравнение декомпозиции:
для упрощения принято, что размер n равен степени b.
Порядок роста зависит от a, b и f.
©Павловская Т.А. (СПб НИУ ИТМО)
(1)

Основная теорема декомпозиции
Можно указать класс эффективности алгоритма, не решая само рекуррентное уравнение.
Этот подход позволяет установить порядок роста решения, не определяя неизвестные множители.
©Павловская Т.А. (СПб НИУ ИТМО)
(1)

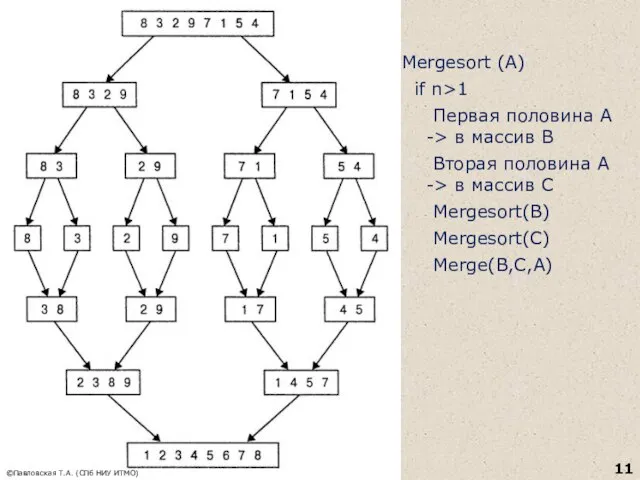
Сортировка слиянием
Сортирует заданный массив путем его разделения на две половины, рекурсивной сортировки каждой половины и слияния двух отсортированных половин в один отсортированный массив:
Mergesort (A)
if n>1
Первая половина А -> в массив В
Вторая половина А -> в массив С
Mergesort(B)
Mergesort(C)
Меrgе(В,С,А) // слить
©Павловская Т.А. (СПб НИУ ИТМО)

©Павловская Т.А. (СПб НИУ ИТМО)
Mergesort (A)
if n>1
Первая половина А -> в массив В
Вторая половина А -> в массив С
Mergesort(B)
Mergesort(C)
Меrgе(В,С,А)

Слияние массивов
Два индекса массивов после инициализации указывают на первые элементы сливаемых массивов.
Элементы сравниваются, и меньший из них добавляется в новый массив.
Индекс меньшего элемента увеличивается (он указывает на элемент, непосредственно следующий за только что скопированным).
Эта операция повторяется до тех пор, пока не будет исчерпан один из сливаемых массивов.
Оставшиеся элементы второго массива добавляются в конец нового массива.
©Павловская Т.А. (СПб НИУ ИТМО)

Анализ сортировки слиянием
Пусть длина файла является степенью 2.
Количество сравнений ключей:
C(n) = 2*C(n/2) + Cmerge (n) n > 1, C(1)=0
Cmerge (n) = n-1 в худшем случае (кол-во сравнений ключей при слиянии)
В худшем случае Cw:
Cw(n) = 2*Cw (n/2) +n-1
Cw (n) ∈ Θ(n log n) – по осн. теореме
©Павловская Т.А. (СПб НИУ ИТМО)
(1)
d=1
a=2
b=2

Количество сравнений ключей, выполняемых сортировкой слиянием, в худшем случае весьма близко к теоретическому минимуму количества сравнений для любого алгоритма сортировки, основанного на сравнениях.
Основной недостаток сортировки слиянием — необходимость дополнительной памяти, количество которой линейно пропорционально размеру входных данных.
©Павловская Т.А. (СПб НИУ ИТМО)

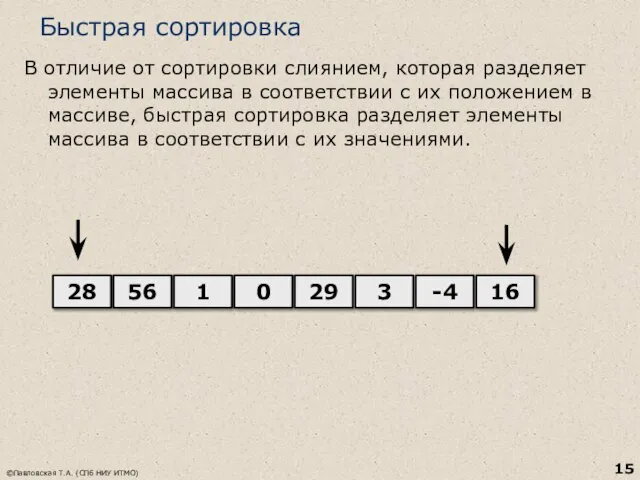
Быстрая сортировка
В отличие от сортировки слиянием, которая разделяет элементы массива в соответствии с иx положением в массиве, быстрая сортировка разделяет элементы массива в соответствии с их значениями.
©Павловская Т.А. (СПб НИУ ИТМО)
28
1
0
29
3
-4
16
56

Описание алгоритма
Выбираем опорный элемент
Выполняем перестановку элементов для получения разбиения, когда все элементы до некоторой позиции s не превышают элемента A [s], а элементы после позиции s не меньше него.
Очевидно, что после разбиения A [s] находится в окончательной позиции, и мы можем сортировать два подмассива элементов до и после A [s] независимо (тем же или другим методом)
©Павловская Т.А. (СПб НИУ ИТМО)

Процедура перестановки элементов
Эффективный метод, основанный на двух проходах подмассива — слева направо и справа налево. При каждом проходе элементы сравниваются с опорным.
Проход слева направо (i) пропускает элементы, меньшие опорного, и останавливается на первом элементе, не меньшем опорного.
Проход справа налево (j) пропускает элементы, большие опорного, и останавливается на первом элементе, не превышающем опорный.
Если индексы сканирования не пересеклись, обмениваем найденные элементы местами и продолжаем проходы.
Если индексы пересеклись, обмениваем опорный элемент с Aj
©Павловская Т.А. (СПб НИУ ИТМО)

Эффективность быстрой сортировки
Наилучший случай: все разбиения оказываются посередине соответствующих подмассивов
В наихудшем случае все разбиения оказываются такими, что один из подмассивов пуст, а размер второго на 1 меньше размера разбиваемого массива (зависимость квадратичная).
В среднем случае считаем, что разбиение может выполняться в каждой позиции с одинаковой вероятностью:
Cavg ≈ 2 n ln n ≈ 1,38 n log2 n
©Павловская Т.А. (СПб НИУ ИТМО)

Улучшения алгоритма
улучшенные методы выбора опорного элемента
переключение на более простую сортировку для малых подмассивов
удаление рекурсии
Все вместе эти улучшения могут снизить время работы алгоритма на 20-25% (Р. Седжвик)
©Павловская Т.А. (СПб НИУ ИТМО)

Обход бинарного дерева
Это еще один пример применения метода декомпозиции
При обходе в прямом порядке сначала посещается корень дерева, а затем левое и правое поддеревья.
При симметричном обходе корень посещается после левого поддерева, но перед посещением правого.
При обходе в обратном порядке корень посещается после левого и правого поддеревьев.
©Павловская Т.А. (СПб НИУ ИТМО)

©Павловская Т.А. (СПбГУ ИТМО)
Обход дерева
procedure print_tree( дерево );
begin
print_tree( левое_поддерево )
посещение корня
print_tree( правое_поддерево )
end;
1
6
8
10
20
21
25
30

Метод уменьшения размера задачи
©Павловская Т.А. (СПб НИУ ИТМО)

Метод уменьшения размера задачи
Основан на использовании связи между решением данного экземпляра задачи и решением меньшего экземпляра той же задачи.
Если такая связь установлена, ее можно использовать либо сверху вниз (рекурсивно), либо снизу вверх (без рекурсии).
(пример – возведение числа в степень)
Имеется три основных варианта метода уменьшения размера:
уменьшение на постоянную величину (обычно на 1);
уменьшение на постоянный множитель (обычно в 2 раза);
уменьшение переменного размера.
©Павловская Т.А. (СПб НИУ ИТМО)

Сортировка вставкой
Предположим, что задача сортировки массива размерностью n-1 решена. Тогда остается вставить An в нужное место:
Просматривая массив слева направо
Просматривая массив справа налево
Используя бинарный поиск места вставки
Хотя сортировка вставкой основана на рекурсивном подходе, более эффективной будет ее реализация снизу вверх (итеративная).
©Павловская Т.А. (СПб НИУ ИТМО)

Реализация на псевдокоде
for i = 1 to n — 1 do v <— A[i]
j <— i-1
while j >= 0 and A[j] > v do
A[j + 1] <— A[j]
j <— j-1
A[j + 1] <— v
©Павловская Т.А. (СПб НИУ ИТМО)

Эффективность сортировки вставкой
Наихудший случай: выполняется столько же сравнений, сколько и в сортировке выбором
Наилучший случай (для изначально отсортированного массива): сравнение выполняется только 1 раз для каждого прохода внешнего цикла
Средний случай (случайный массив): выполняется в ~2 раза меньше сравнений, чем в случае убывающего массива.
Т.о., средний случай в 2 раза лучше наихудшего. Вкупе с превосходной производительностью для почти отсортированных массивов это выделяет сортировку вставкой из других элементарных (выбором и пузырьком) алгоритмов
Модификация метода – вставка одновременно нескольких элементов, которые перед вставкой сортируются.
Расширение сортировки вставкой — сортировка Шелла, дает еще лучший алгоритм для сортировки достаточно больших файлов.
©Павловская Т.А. (СПб НИУ ИТМО)

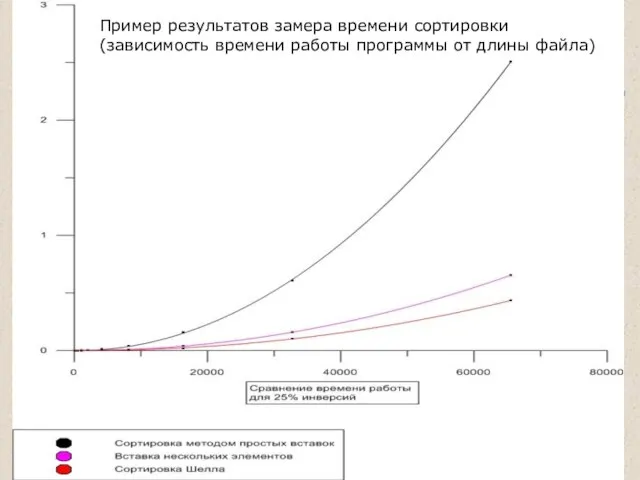
Пример результатов замера времени сортировки
(зависимость времени работы программы от длины файла)

Генерация комбинаторных объектов
Наиболее важными типами комбинаторных объектов являются перестановки, сочетания и подмножества данного множества.
Обычно они возникают в задачах, требующих рассмотрения различных вариантов выбора.
Кроме того, существуют понятия размещения и разбиения.
©Павловская Т.А. (СПб НИУ ИТМО)

Генерация перестановок
Число перестановок
Пусть дан n-элементный набор (множество).
На первом месте в перестановке может стоять любой элемент, то есть существует n способов выбора первого элемента.
Осталось (n-1) элементов для выбора второго элемента в перестановке (существует (n-1) способов выбора второго элемента).
Осталось (n-2) элемента для выбора третьего элемента в перестановке, и т.д.
Итого, n-элементный упорядоченный набор можно получить:
способами
©Павловская Т.А. (СПб НИУ ИТМО)

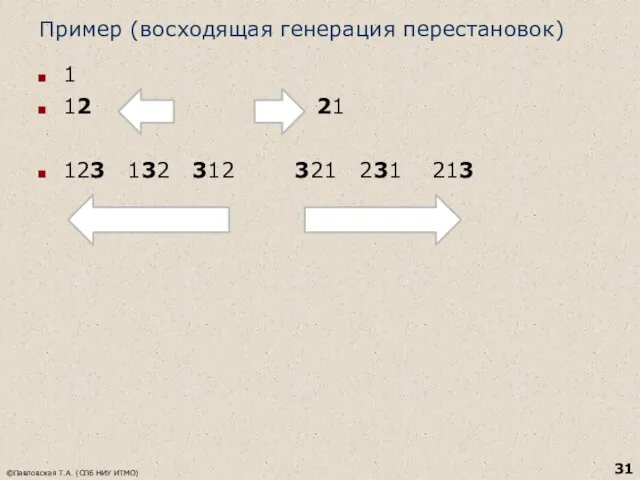
Применение метода уменьшения размера к задаче получения всех перестановок
Для простоты положим, что множество переставляемых элементов — это множество целых чисел от 1 до n.
Задача меньшего на единицу размера состоит в генерации всех (n — 1)! перестановок.
Полагая, что она решена, мы можем получить решение большей задачи путем вставки n в каждую из n возможных позиций среди элементов каждой из перестановок n — 1 элементов.
Все получаемые таким образом перестановки будут различны, а их общее количество:
n(n— 1)! = n!
Можно вставлять n в ранее сгенерированные перестановки слева направо или справа налево. Выгодно начинать справа налево и изменять направление всякий раз при переходе к новой перестановке множества {1,...,n —1}.
©Павловская Т.А. (СПб НИУ ИТМО)

Пример (восходящая генерация перестановок)
1
12 21
123 132 312 321 231 213
©Павловская Т.А. (СПб НИУ ИТМО)

Алгоритм Джонсона-Троттера
Вводится понятие мобильного элемента. С каждым элементом связывается стрелка, элемент считается мобильным, если стрелка указывает на меньший соседний элемент.
Инициализируем первую перестановку значением 1 2 ... n (все стрелки влево)
while имеется мобильное число к do
Находим наибольшее мобильное число к
Меняем местами к и соседнее число, на которое указывает стрелка к
Меняем направление стрелок у всех чисел, больших к
©Павловская Т.А. (СПб НИУ ИТМО)

Лексикографический порядок
Пусть есть первая перестановка (например, 1234).
Для нахождения каждой следующей:
1. Cканируем текущую перестановку справа налево в поисках первой пары соседних элементов таких, что a[i] < a[i+1].
Для перестановки 1234 это число 3 (3 < 4).
2. Находим наименьший элемент из "хвоста", больший a[i], и помещаем его в позицию i. В первый раз на место 3 ставим 4.
3. Позиции с i+1 по n заполняем элементами а[i], a[i+1],..., а[n], из которых изъят помещенный в позицию i элемент, в возрастающем порядке. В данном случае 3.
©Павловская Т.А. (СПб НИУ ИТМО)
1
2
3
4

Пример для осознания алгоритма
1234 1243 1324 1342 1423 1432
2134 2143 2314 2341 2413 2431
3124 3142 3214 3241 3412 3421
4123 4132 4213 4231 4312 4321
©Павловская Т.А. (СПб НИУ ИТМО)

Число всех перестановок из n элементов
Р(n) = n!
©Павловская Т.А. (СПб НИУ ИТМО)

Подмножества множества
Множество A является подмножеством множества B, если любой элемент, принадлежащий A, также принадлежит B:
A ⊂ B или A ⊆ B
Любое множество является своим подмножеством. Пустое множество является подмножеством любого множества.
Множество всех подмножеств множества обозначается 2A (еще его называют power set, множество-степень, степень множества, булеан, показательное множество).
Число подмножеств конечного множества, состоящего из n элементов, равно 2n (доказательство см. в Википедии ☺ )
©Павловская Т.А. (СПб НИУ ИТМО)

Генерация всех подмножеств множества
Применим метод уменьшения размера задачи на 1.
Все подмножества множества А = {a1,..., аn} можно разделить на две группы — которые содержат элемент аn и которые его не содержат.
Первая группа – это все подмножества множества {a1,... ,an-1}; все элементы второй группы можно получить путем добавления элемента аn к подмножествам первой группы.
∅
∅ {a1}
∅ {a1} {a2} {a1, a2}
∅ {a1} {a2} {a1, a2} {a3} {a1, a3} {a2, a3} {a1, a2, a3}
Удобно поставить в соответствие элементам множества битовые строки:
000 001 010 011 100 101 110 111
Иные порядки: плотный; код Грея:
000 001 011 010 110 111 101 100
©Павловская Т.А. (СПб НИУ ИТМО)

Генерация кодов Грея
Код Грея для n бит может быть рекурсивно построен на основе кода для n–1 бит путём:
записывания кодов в обратном порядке
конкатенации исходного и перевёрнутого списков
дописывания 0 в начало каждого кода в исходном списке и 1 в начало кодов в перевёрнутом списке.
Пример:
Коды для n = 2 бит: 00, 01, 11, 10
Перевёрнутый список кодов: 10, 11, 01, 00
Объединённый список: 00, 01, 11, 10, 10, 11, 01, 00
К начальному списку дописаны нули: 000, 001, 011, 010, 10, 11, 01, 00
К перевёрнутому списку дописаны единицы: 000, 001, 011, 010, 110, 111, 101, 100
©Павловская Т.А. (СПб НИУ ИТМО)

K-элементные подмножества
Количество k-элементных подмножеств множества n (0≤k≤n) называется числом сочетаний (биномиальным коэффициентом):
Прямое решение неэффективно из-за быстрого роста факториала.
Как правило, генерацию k-элементных подмножеств проводят в лексикографическом порядке (для любых двух подмножеств первым генерируется то, из индексов элементов которого можно составить меньшее k-значное число в n-ричной системе счисления).
Метод:
первым элементом подмножества мощности k может быть любой из элементов, начиная с первого и заканчивая (n-k+1)-ым.
После того, как индекс первого элемента подмножества зафиксирован, остается выбрать k-1 элемент из элементов с индексами, большими чем у первого.
Далее аналогично, сводя задачу к меньшей размерности до тех пор, пока на низшем уровне рекурсии не будет выбран последний элемент, после чего выбранное подмножество можно распечатать или обработать.
©Павловская Т.А. (СПб НИУ ИТМО)

Пример: сочетания из 6 по 3
#include
const int N = 6, K = 3;
int a[K];
void rec(int i)
{ if (i == K)
{ for (int j = 0; j < K; j++) printf("%d ", a[j]); printf("\n"); }
else
{ for (a[i] = (i > 0 ? a[i-1] + 1 : 1); a[i] < N; a[i]++) rec(i + 1); }
}
int main() { int a[N]; rec(0); }
©Павловская Т.А. (СПб НИУ ИТМО)
1 2 3
1 2 4
1 2 5
1 3 4
1 3 5
1 4 5
2 3 4
2 3 5
2 4 5
3 4 5

Свойства сочетаний
каждому n-элементному подмножеству данного элементного множества соответствует одно и только одно n-k-элементное подмножество того же множества:
©Павловская Т.А. (СПб НИУ ИТМО)

Треугольник Паскаля
©Павловская Т.А. (СПб НИУ ИТМО)

Свойства треугольника Паскаля (Википедия)
©Павловская Т.А. (СПб НИУ ИТМО)

Размещения
Размещением из n элементов по m называется последовательность, состоящая из m различных элементов некоторого n-элементного множества (комбинации, которые составлены из данных n элементов по m элементов и отличаются либо самими элементами, либо порядком элементов)
Различие в определениях сочетаний и размещений:
Сочетание – подмножество, содержащее m элементов из n (порядок элементов не важен).
Размещение – это последовательность, содержащая m элементов из n (порядок элементов важен).
При формировании последовательности важен порядок следования элементов, а при формировании подмножества порядок не важен.
©Павловская Т.А. (СПбГУ ИТМО)

Число размещений
Число размещений из n по m:
Пример 1: Сколько существует двузначных чисел, в которых цифра десятков и цифра единиц различны и нечетны?
Основное множество: {1, 3, 5, 7, 9} – нечетные цифры, n=5
Соединение – двузначное число m=2, порядок важен, значит, это размещение «из пяти по два».
Перестановки можно считать частным случаем размещений при m=n
Пример 2: Сколькими способами можно составить флаг, состоящий из трех горизонтальных полос различных цветов, если имеется материал пяти цветов?
©Павловская Т.А. (СПб НИУ ИТМО)

Размещения с повторениями
Размещения с повторениями из n элементов множества Е={a1, a2, ..., an} по k - всякая конечная последовательность, состоящая из k элементов данного множества Е.
Два размещения с повторениями считаются различными, если хотя бы на одном месте они имеют различные элементы множества Е.
Число различных размещений с повторениями из n по k равно nk.
©Павловская Т.А. (СПб НИУ ИТМО)

Разбиение множеств
Разбиение множества — это представление его в виде объединения произвольного количества попарно непересекающихся подмножеств.
©Павловская Т.А. (СПб НИУ ИТМО)
Количество неупорядоченных разбиений n-элементного множества на k частей - число Стирлинга 2-го рода:
Количество упорядоченных разбиений n-элементного множества на m частей фиксированного размера – мультиномиальный коэффициент:
Количество всех неупорядоченных разбиений n-элементного множества задается числом Белла:

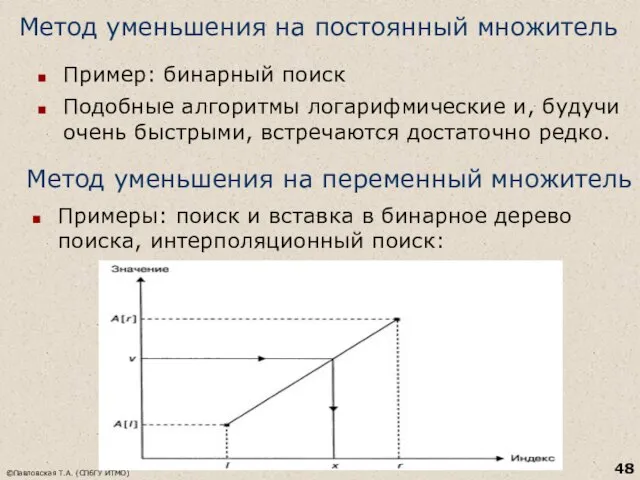
Метод уменьшения на постоянный множитель
Пример: бинарный поиск
Подобные алгоритмы логарифмические и, будучи очень быстрыми, встречаются достаточно редко.
©Павловская Т.А. (СПбГУ ИТМО)
Метод уменьшения на переменный множитель
Примеры: поиск и вставка в бинарное дерево поиска, интерполяционный поиск:

Анализ эффективности
Интерполяционный поиск в среднем требует менее log2 log2 n+1 сравнений ключей при поиске в списке из n случайных значений.
Эта функция растет настолько медленно, что для всех реальных практических значений n ее можно считать константой.
Однако в наихудшем случае интерполяционный поиск вырождается в линейный, который рассматривается как наихудший из возможных.
Интерполяционный поиск лучше использовать для файлов большого размера и для приложений, в которых сравнение или обращение к данным — дорогостоящая операция.
©Павловская Т.А. (СПб НИУ ИТМО)

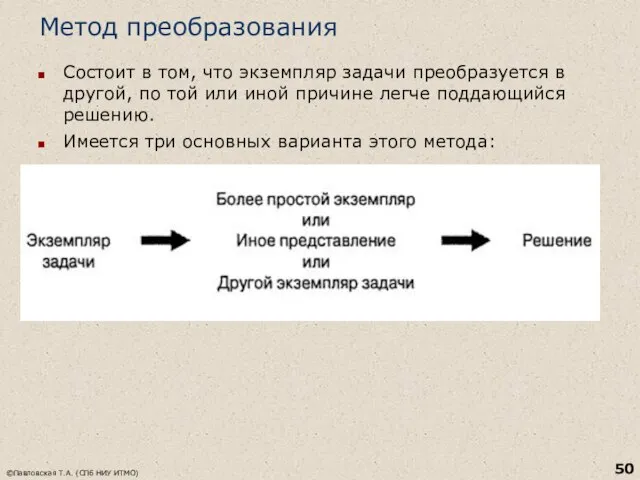
Метод преобразования
Состоит в том, что экземпляр задачи преобразуется в другой, по той или иной причине легче поддающийся решению.
Имеется три основных варианта этого метода:
©Павловская Т.А. (СПб НИУ ИТМО)

Пример 1: проверка единственности элементов массива
Алгоритм на основе грубой силы попарно сравнивает все элементы, пока не будут найдены два одинаковых либо пока не будут пересмотрены все возможные пары. В наихудшем случае эффективность квадратична.
К решению задачи можно подойти и по-другому — сначала отсортировать массив, а затем сравнивать только последовательные элементы.
Время работы алгоритма - сумма времени сортировки и времени на проверку соседних элементов.
Если воспользоваться хорошим алгоритмом сортировки, весь алгоритм проверки единственности элементов массива также будет иметь эффективность О (n log n)
©Павловская Т.А. (СПб НИУ ИТМО)

Пример 2: поиск
Метод грубой силы: последовательный поиск
Метод преобразования задачи: сортировка + бинарный поиск
Требуется оценить наименьшее количество поисков, при котором окупается предварительная сортировка
©Павловская Т.А. (СПб НИУ ИТМО)