МЕХАНИЧЕСКИЕ КОЛЕБАНИЯ и волны

ЛИТЕРАТУРА
1.Ремизов А.Н., Максина А.Г., Потапенко А.Я. Медицинская и биологическая физика. М., «Дрофа», 2008, §§ 5.1.-5.8.
2. Ремизов А.Н., Потапенко А.Я. Курс физики. М., «Дрофа», 2004, §§ 6.1.-6.6.
3. Физика и биофизика (под ред. Антонова В.Ф.). М., «ГЭОТАР-Медиа», 2008, §§ 1.1.-1.6, 2.1, 2.2.

1.Основные понятия и определения колебательных процессов
Колебаниями называются движения или изменения состояния, обладающие той или иной степенью повторяемости во времени.
Колебания присущи всем явлениям природы: колеблется температура воздуха, вода в морях и океанах, магнитное поле Земли, пульсирует излучение звезд, внутри которых происходят циклические ядерные реакции, с высокой степенью точности вращаются планеты Солнечной системы, движение Луны вызывает приливы и отливы на Земле.

В любом живом организме – от одиночной клетки до их высокоорганизованных популяций - непрерывно происходят разнообразные, ритмично повторяющиеся процессы: биение сердца, артериальный пульс, создание звуков голосовыми связками и т.д.
Колебания разнообразны по своей физической природе: механические колебания тела, подвешенного на пружине (пружинный маятник), качания маятников, колебания струн, вибрации фундаментов зданий, электромагнитные колебания в колебательном контуре и др. Разнообразные по природе, колебания могут иметь общие закономерности и описываться однотипными математическими методами.
Колебания бывают периодическими и непериодическими.

Последние можно разложить на периодические составляющие, поэтому мы здесь будем рассматривать только периодические колебания.
Если значения физических величин, изменяющихся в процессе колебаний, повторяются через равные промежутки времени, то колебания называются периодическими.
Время, за которое совершается одно полное колебание, называется периодом колебания Т.
Число полных колебаний, совершающихся за единицу времени, называется частотой периодических колебаний ν:

Циклической или круговой частотой периодических колебаний называется число полных колебаний, совершаемых за 2π единиц времени:
В физике особо выделяются механические и электромагнитные колебания и их комбинации. Это обусловлено той исключительной ролью, которую играют гравитационные и электромагнитные взаимодействия в жизнедеятельности человека. С помощью распространяющихся механических колебаний плотности и давления воздуха, воспринимаемых нами как звук и быстрых колебаний электрических и магнитных полей, воспринимаемых нами как свет, мы получаем большую часть прямой информации об окружающем мире.

Периодические колебания физической величины х, происходящие по закону синуса или косинуса
(1)
(1а)
называются гармоническими.
Здесь А, ω, φ0 - постоянные величины и А>0, ω>0.
Величина А, равная наибольшему абсолютному значению колеблющейся физической величины, называется амплитудой колебаний; φ = ωt+φ0 - фаза колебаний, φ0 - начальная фаза (φ= φ0 при t=0).
Если мы рассматриваем колеблющуюся массу, то х соответствует смещению массы от положения равновесия, в случае колебательного контура х - это либо заряд на обкладках конденсатора, либо ток в катушке индуктивности.

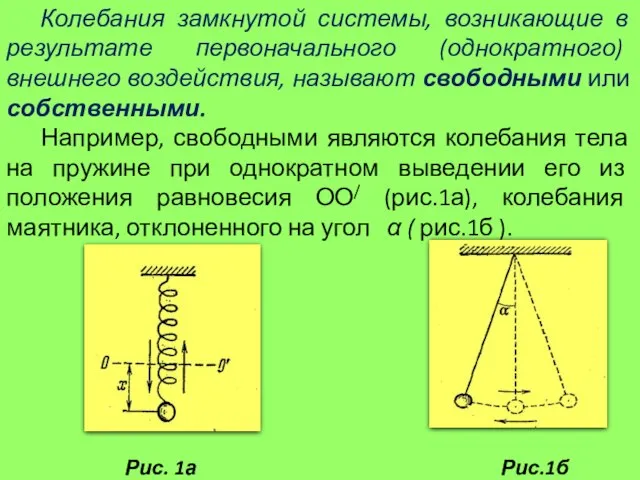
Колебания замкнутой системы, возникающие в результате первоначального (однократного) внешнего воздействия, называют свободными или собственными.
Например, свободными являются колебания тела на пружине при однократном выведении его из положения равновесия ОО/ (рис.1а), колебания маятника, отклоненного на угол α ( рис.1б ).
Рис. 1а Рис.1б

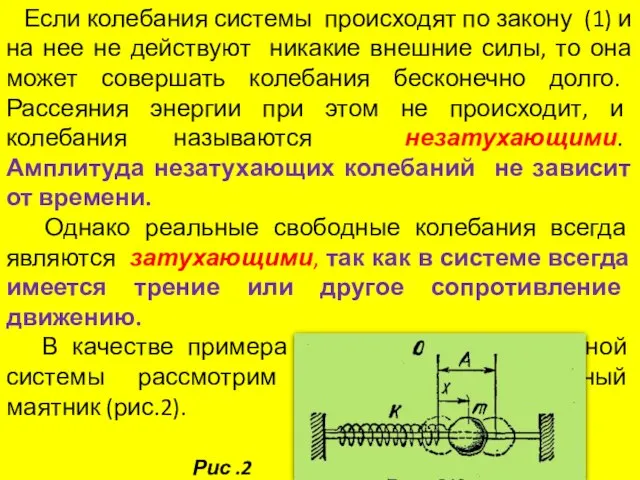
Если колебания системы происходят по закону (1) и на нее не действуют никакие внешние силы, то она может совершать колебания бесконечно долго. Рассеяния энергии при этом не происходит, и колебания называются незатухающими. Амплитуда незатухающих колебаний не зависит от времени.
Однако реальные свободные колебания всегда являются затухающими, так как в системе всегда имеется трение или другое сопротивление движению.
В качестве примера простейшей колебательной системы рассмотрим горизонтальный пружинный маятник (рис.2).
Рис .2

Шарик массой m может скользить без трения по горизонтальному стержню. Силу тяжести можно не учитывать, так как она уравновешивается реакцией стержня. К стенке и шарику прикреплена пружина жесткостью k пренебрежимо малой массы. Таким образом, всю массу можно считать сосредоточенной в шарике, а всю жесткость в пружине. В положении равновесия шарика О растяжение пружины равно нулю. Смещение шарика х в любой момент времени равно деформации пружины. На шарик действует сила упругости пружины по закону Гука:
Но по второму закону Ньютона

где m - масса шарика, - его ускорение. Следовательно
Но ускорение есть вторая производная по времени от смещения, и с учетом одномерности движения можно записать
(3)
Это уравнение гармонических колебаний пружинного маятника. Решение его имеет вид
(4)
где
Таким образом, мы получили закон колебаний пружинного маятника в форме синусоиды (рис.3):

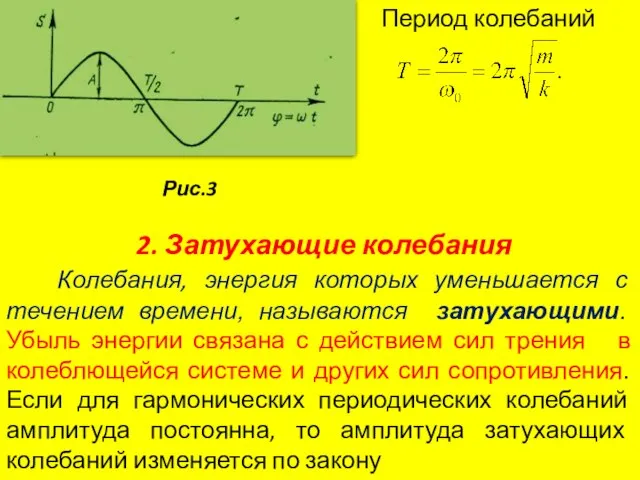
Рис.3
2. Затухающие колебания
Колебания, энергия которых уменьшается с течением времени, называются затухающими. Убыль энергии связана с действием сил трения в колеблющейся системе и других сил сопротивления. Если для гармонических периодических колебаний амплитуда постоянна, то амплитуда затухающих колебаний изменяется по закону
Период колебаний

(5)
где А0 - начальная амплитуда колебаний в момент времени t = 0, δ-коэффициент затухания, который зависит от сил трения и массы колеблющегося тела. При не слишком больших скоростях силу трения можно считать пропорциональной скорости колебаний v, т.е. Fтр = - rv, где r - коэффициент трения, и в этом случае
где m -масса тела.
Значения физических величин, характеризующих затухающие колебания, никогда не повторяются, т.е. затухающие колебания являются непериодическими.

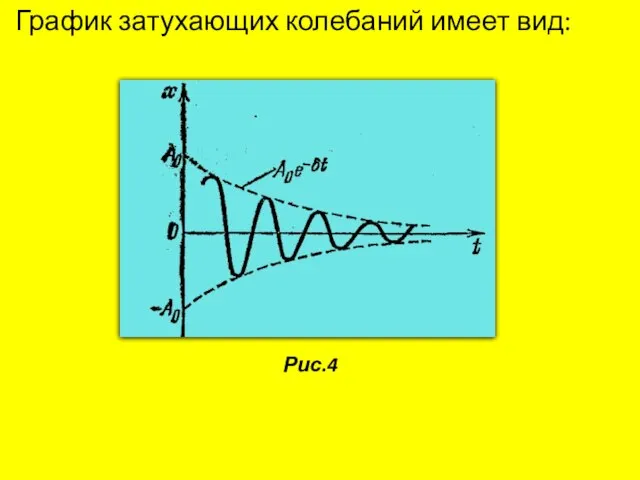
График затухающих колебаний имеет вид:
Рис.4

3. Вынужденные колебания. Автоколебания. Резонанс
Незатухающие колебания системы, вызываемые действием на нее внешней периодической силы F(t), называются вынужденными.
Сила F(t) называется возмущающей или вынуждающей силой.
Если F(t) меняется по гармоническому закону
(6)
то соответствующие вынужденные колебания могут быть также гармоническими с частотой вынуждающей силы:
(7)
где А - амплитуда вынужденных колебаний физической величины, φ1 - разность фаз между вынужденными колебаниями величины х и силы F(t).

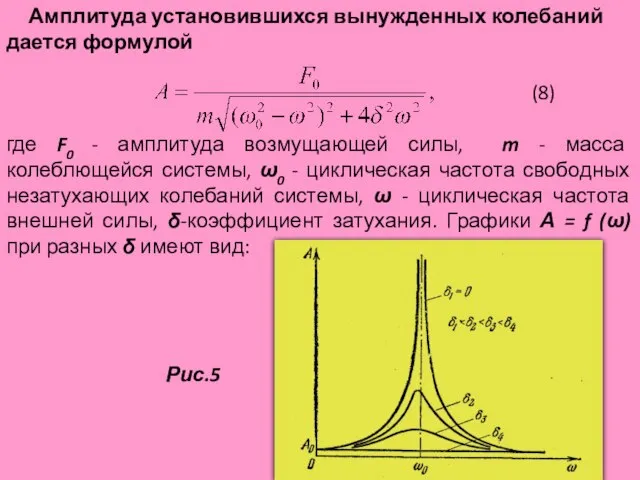
Амплитуда установившихся вынужденных колебаний дается формулой
(8)
где F0 - амплитуда возмущающей силы, m - масса колеблющейся системы, ω0 - циклическая частота свободных незатухающих колебаний системы, ω - циклическая частота внешней силы, δ-коэффициент затухания. Графики А = f (ω) при разных δ имеют вид:
Рис.5

Разберем различные случаи:
1) При ω = 0 А=A0 = F0 /mω02 . При этом колебания не совершаются и отклонение системы из положения равновесия называется статическим отклонением.
2) δ = 0 (отсутствует затухание). Амплитуда вынужденных колебаний А растет с увеличением ω, а при ω = ω0 А→ ∞. С дальнейшим ростом ω амплитуда А уменьшается.
3) δ ≠ 0 - затухание существует. Амплитуда вынужденных колебаний А максимальна при
ω = ωрез = ω0 (9)
Явление возрастания амплитуды вынужденных колебаний при приближении циклической частоты вынуждающей силы к значению ωрез называется резонансом.
,
,
,

Величина ωрез называется резонансной циклической частотой, а кривые зависимости А от ω (рис. 5) – резонансными кривыми.
Форма резонансных кривых зависит от величины коэффициента затухания δ .
Резонанс может иметь место в различных сооружениях и машинах, когда в них периодически меняются нагрузки.
С явлением резонанса приходится считаться при движении любых машин: вибрации, возникающие при работе двигателя, могут стать опасными, если они будут в резонансе с какими-либо из собственных колебаний конструкции.

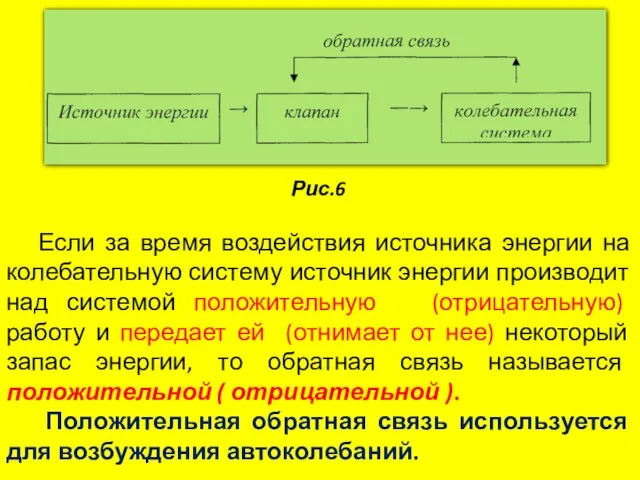
Система, совершающая незатухающие колебания за счет действия источника энергии, не обладающего колебательными свойствами, называется автоколебательной системой.
Любая автоколебательная система состоит из четырех частей:
колебательная система,
источник энергии, который компенсирует потери энергии на затухание колебаний за счет трения или других сил сопротивления,
клапан – устройство, регулирующее поступление энергии в систему определенными порциями,
обратная связь – устройство для обратного воздействия автоколебательной системы на клапан, управления работой клапана за счет процессов в самой колебательной системе.

Рис.6
Если за время воздействия источника энергии на колебательную систему источник энергии производит над системой положительную (отрицательную) работу и передает ей (отнимает от нее) некоторый запас энергии, то обратная связь называется положительной ( отрицательной ).
Положительная обратная связь используется для возбуждения автоколебаний.

В случае отрицательной обратной связи усиливается затухание и автоколебания подавляются.
Автоколебательными системами являются, например, часы, паровые машины и двигатели внутреннего сгорания, отбойные молотки, электрические звонки. Автоколебания совершают струны под действием смычка в скрипке, воздушные столбы в трубах духовых инструментов, голосовые связки при разговоре или пении. Электрической автоколебательной системой является генератор незатухающих электрических колебаний.

3.Механические (упругие) волны. Основные характеристики волн
Среда называется упругой, если между ее частицами существуют силы взаимодействия, препятствующие какой-либо деформации этой среды.
Пусть какое-либо тело совершает колебания в упругой среде. Тогда оно воздействует на частицы среды, прилегающие к нему и заставляет совершать их вынужденные колебания. Среда вблизи колеблющегося тела деформируется и в ней возникают упругие силы, которые действуют на все более удаленные точки среды, выводя их из положения равновесия. Таким образом, с течением времени все частицы среды вовлекаются в колебательное движение.

Для распространения колебаний необязательно наличие упругой среды. Например, электромагнитные колебания могут распространяться и в вакууме.
Любое возмущение состояния вещества или поля, распространяющиеся в пространстве с течением времени называются волнами.
Так, звуковые волны в газах или жидкостях – это колебания давления в этих средах.
Механические возмущения, распространяющиеся в упругой среде, называются упругими волнами.
Тело, вызывающее возмущение среды, называется источником волн.
Геометрическое место точек среды, колеблющихся в одинаковых фазах, называется фронтом волны или волновой поверхностью.

Например, в плоской волне волновыми поверхностями являются плоскости, перпендикулярные направлению распространения волны, а в сферической волне – сферы. Сферические волны порождаются точечным источником (например, волны на поверхности воды, возникающие от брошенного камня).
Волны бывают продольными и поперечными.
Если частицы среды колеблются в направлении, перпендикулярном направлению распространения волны, то волна называется поперечной.
Например, волна, распространяющаяся вдоль натянутого резинового шнура с одним закрепленным концом, является поперечной.
В продольной волне колебания частиц среды происходят в направлении распространения волны.

Скоростью (фазовой скоростью) волны v называется физическая величина равная расстоянию, которое за единицу времени проходит любая точка волновой поверхности. Вектор скорости направлен перпендикулярно к фронту волны в сторону распространения волны.
Длиной волны λ называется расстояние между двумя ближайшими точками, колеблющимися в одинаковой фазе (или со сдвигом фаз Δφ=2π). Другими словами, длина волны – это расстояние, на которое распространяется фронт волны за один период колебаний источника волн:
где v – скорость распространения волн, ν=1/Т –частота колебаний в источнике, ω – циклическая частота. Частота колебаний зависит только от свойств источника волн. От свойств среды зависит скорость распространения волн и, вследствие этого, длина волны.

4.Уравнение плоской волны. Энергия и интенсивность волны. Вектор Умова
Пусть в источнике волн изменения колеблющейся величины происходят по закону
(10)
с амплитудой А, циклической частотой ω и начальной фазой φ. Тогда колебания частиц фронта плоской волны в точке, отстоящей на расстояние х от источника, запаздывают по времени на Δt:
(11)
При этом предполагается, что в процессе распространения волны не происходит ее затухания.

Уравнение плоской синусоидальной волны, распространяющейся вдоль оси Ох имеет вид
(12) Величина
(13)
называется волновым числом. Оно показывает, сколько длин волн укладывается на расстоянии, равном 2π единиц длины. С учетом этого, уравнение плоской волны можно переписать в виде
(14)

Колеблющийся источник волн обладает энергией. В процессе распространения волны каждая частица среды, до которой доходит волна, также колеблется и имеет энергию.
Выделим некоторый объем V упругой среды, в которой распространяется волна с амплитудой A и циклической частотой ω. В этом объеме имеется средняя энергия
(15)
где m - масса выделенного объема среды.
Средняя плотность энергии волны есть энергия волны, сосредоточенная в единице объема среды:
(16)

где ρ - плотность среды.
Интенсивностью волны I называется величина, равная энергии, которую в среднем переносит волна за единицу времени через единицу площади поверхности, перпендикулярной к направлению распространения волны:
(17)
где ʋ- скорость распространения волны. В векторной форме
(18)
называется вектором Умова.