Механические колебания и волны

Содержание
1. Колебания
2. Виды колебаний
2.1. Свободные колебания
2.2. Математический маятник
2.3. Пружинный маятник
3. Гармонические колебания
3.1. Понятие
3.2. Уравнение и графики
3.3. Превращение энергии
4. Вынужденные колебания
4.1. Собственная частота
4.2. Резонанс
5. Автоколебания
6. Волны
7. Поперечные и продольные волны
8. Волны в среде
9. Звуковые волны
10. Свойства волн
10.1. отражение и преломление волн
10.2. Интерференция волн
10.3.Дифракция волн
10.4. Поляризация волн

1. Колебания
Колебания – это движения или процессы, которые точно или приблизительно повторяются через определенные интервалы времени.
Механические колебания и волны –
раздел механики, изучающий особый вид движения – колебания, а так же распространение колебаний в пространстве

Механические колебания
Колебания механических величин (смещения, скорости, ускорения, энергии и т. п.)
Виды колебаний
Свободные
Вынужденные
Автоколебания
Колебательная система –
это система тел, совершающих колебание.

Свободные
Колебания, возникающие при однократном воздействии внешней силы (первоначальном сообщении энергии) и при отсутствии внешних воздействий на колебательную систему.
Условия возникновения свободных колебаний
1. Колебательная система должна иметь положение устойчивого равновесия.
2. При выведении системы из положения равновесия должна возникать равнодействующая сила, возвращающая систему в исходное положение
3. Инертность системы
4. Силы трения (сопротивления) очень малы.

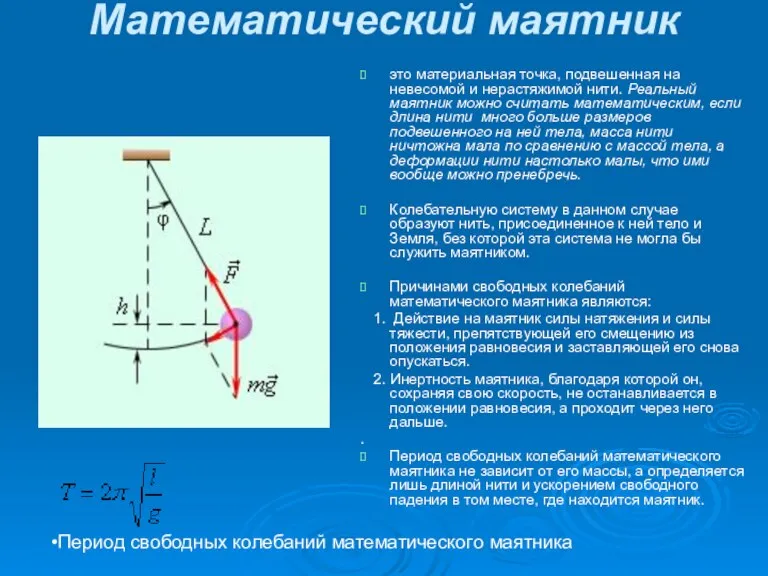
Математический маятник
это материальная точка, подвешенная на невесомой и нерастяжимой нити. Реальный маятник можно считать математическим, если длина нити много больше размеров подвешенного на ней тела, масса нити ничтожна мала по сравнению с массой тела, а деформации нити настолько малы, что ими вообще можно пренебречь.
Колебательную систему в данном случае образуют нить, присоединенное к ней тело и Земля, без которой эта система не могла бы служить маятником.
Причинами свободных колебаний математического маятника являются:
1. Действие на маятник силы натяжения и силы тяжести, препятствующей его смещению из положения равновесия и заставляющей его снова опускаться.
2. Инертность маятника, благодаря которой он, сохраняя свою скорость, не останавливается в положении равновесия, а проходит через него дальше.
.
Период свободных колебаний математического маятника не зависит от его массы, а определяется лишь длиной нити и ускорением свободного падения в том месте, где находится маятник.
Период свободных колебаний математического маятника

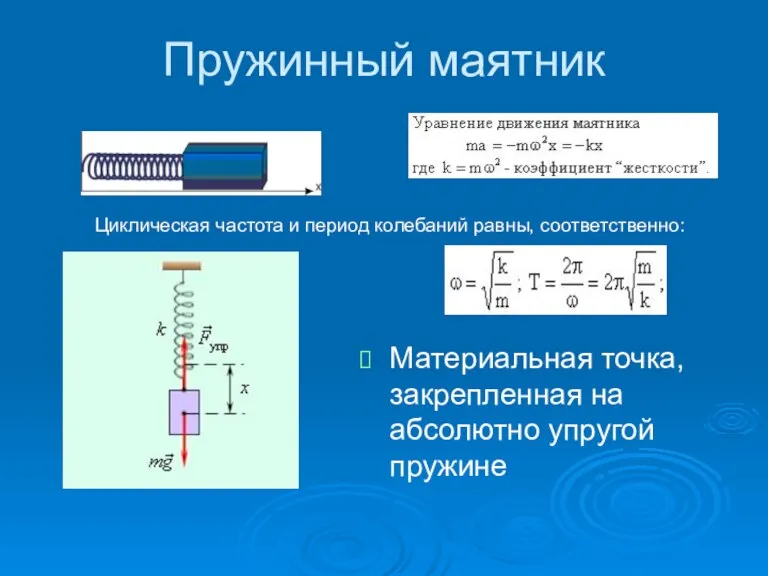
Пружинный маятник
Материальная точка, закрепленная на абсолютно упругой пружине
Циклическая частота и период колебаний равны, соответственно:

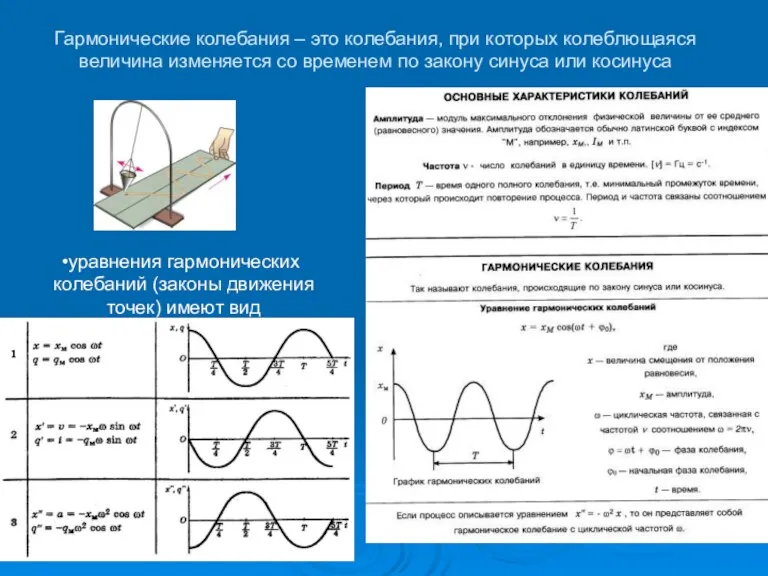
Гармонические колебания – это колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса
уравнения гармонических колебаний (законы движения точек) имеют вид

Превращение энергии
график зависимости потенциальной и кинетической энергии пружинного маятника от координаты х.
качественные графики зависимостей кинетической и потенциальной энергии от времени.

Вынужденные
Колебания, возникающие под действием внешних, периодически изменяющихся сил (при периодическом поступлении энергии извне к колебательной системе)
Частота вынужденных колебаний равна частоте изменения внешней силы
Если Fbc изменяется по закону синуса или косинуса, то вынужденные колебания будут гармоническими

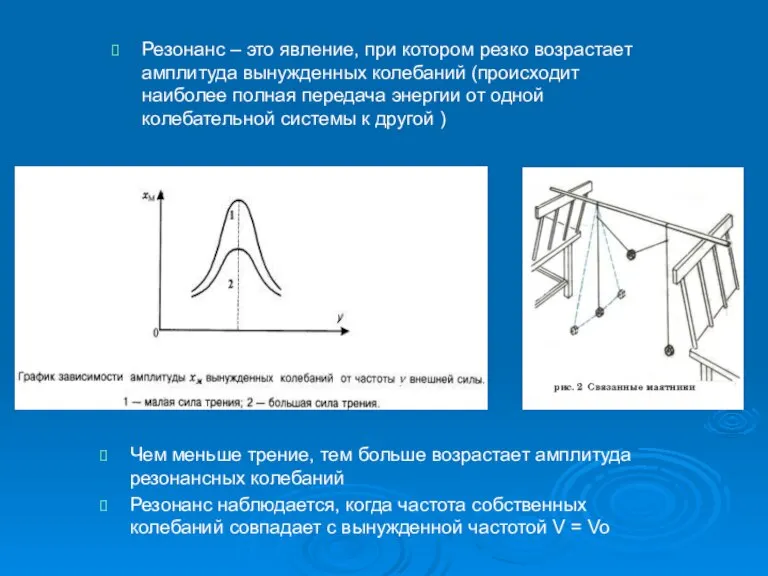
Резонанс – это явление, при котором резко возрастает амплитуда вынужденных колебаний (происходит наиболее полная передача энергии от одной колебательной системы к другой )
Чем меньше трение, тем больше возрастает амплитуда резонансных колебаний
Резонанс наблюдается, когда частота собственных колебаний совпадает с вынужденной частотой V = Vo

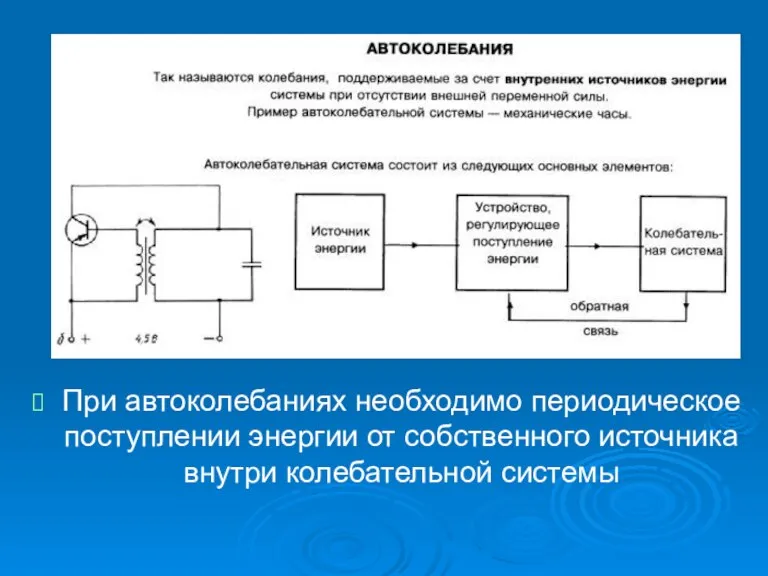
При автоколебаниях необходимо периодическое поступлении энергии от собственного источника внутри колебательной системы

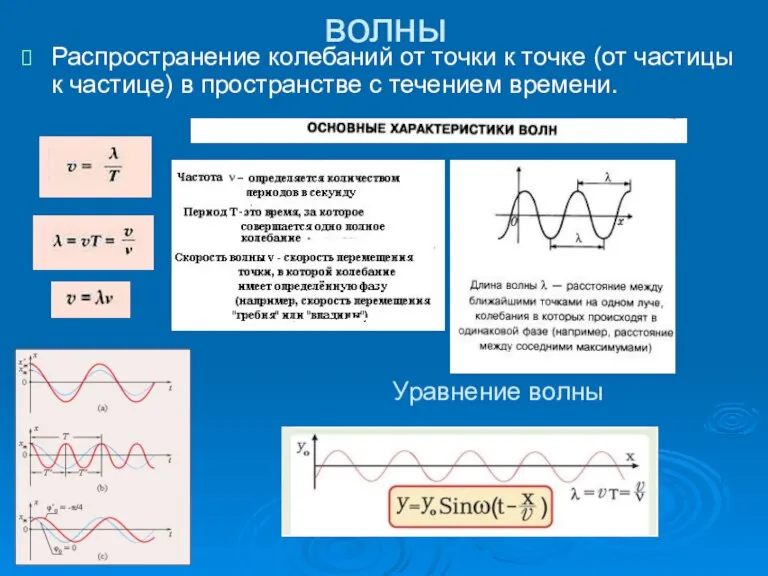
волны
Распространение колебаний от точки к точке (от частицы к частице) в пространстве с течением времени.
Уравнение волны

Поперечные -это волны, в которых частицы среды колеблются перпендикулярно направлению волны,
Деформация сдвига в твердых телах, на поверхности жидкости
Продольные – это волны, в которых частицы среды колеблются вдоль направления распространения волны.
Деформация сжатия в газах, жидкостях, твердых телах
Причины возникновения механических волн
Упругая среда (частицы среды взаимодействуют за счет сил упругости)
Инертность частиц
Волны и энергия
Вместе с колебаниями волной переносится энергия колебаний, хотя сами носители этой энергии, колеблющиеся частицы, с волной не переносятся
Волна является переносчиком энергии

Волны в среде.
Волновая поверхность – геометрическое место точек, колеблющихся в одинаковой фазе
Волновой фронт – геометрическое место точек, до которых доходят колебания к моменту времени t
Луч – линия перпендикулярная волновой поверхности (эта линия показывает направление распространения волны)
Виды волн

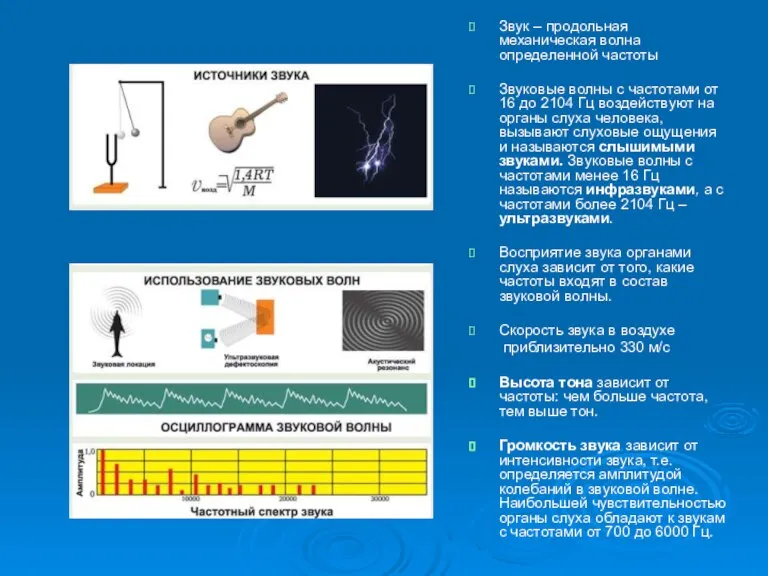
Звук – продольная механическая волна определенной частоты
Звуковые волны с частотами от 16 до 2104 Гц воздействуют на органы слуха человека, вызывают слуховые ощущения и называются слышимыми звуками. Звуковые волны с частотами менее 16 Гц называются инфразвуками, а с частотами более 2104 Гц – ультразвуками.
Восприятие звука органами слуха зависит от того, какие частоты входят в состав звуковой волны.
Скорость звука в воздухе
приблизительно 330 м/с
Высота тона зависит от частоты: чем больше частота, тем выше тон.
Громкость звука зависит от интенсивности звука, т.е. определяется амплитудой колебаний в звуковой волне. Наибольшей чувствительностью органы слуха обладают к звукам с частотами от 700 до 6000 Гц.

Свойства волн
Принцип Гюйгенса
Каждая возбужденная волной точка сама становится источником элементарных волн. Огибающая элементарных волн дает новое положение волнового фронта
Принцип суперпозиции волн
При распространении в среде нескольких волн каждая из них распространяется так, как будто другие волны отсутствуют

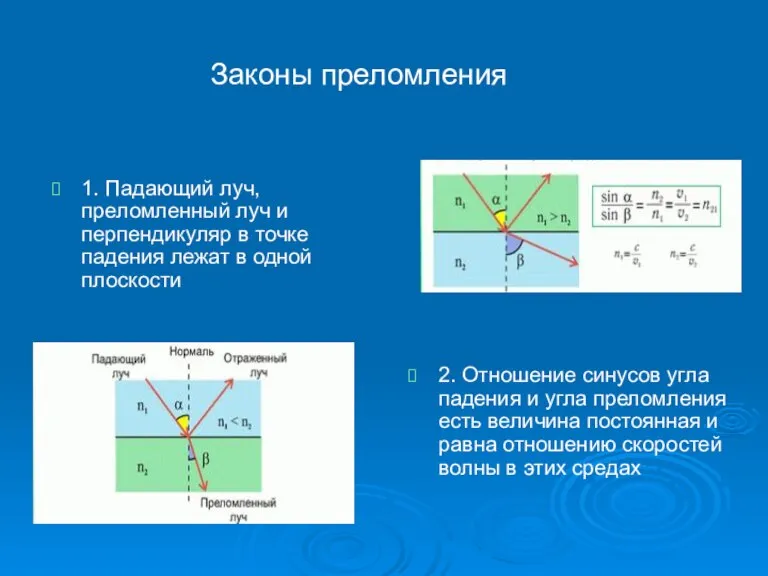
1. Падающий луч, преломленный луч и перпендикуляр в точке падения лежат в одной плоскости
2. Отношение синусов угла падения и угла преломления есть величина постоянная и равна отношению скоростей волны в этих средах
Законы преломления

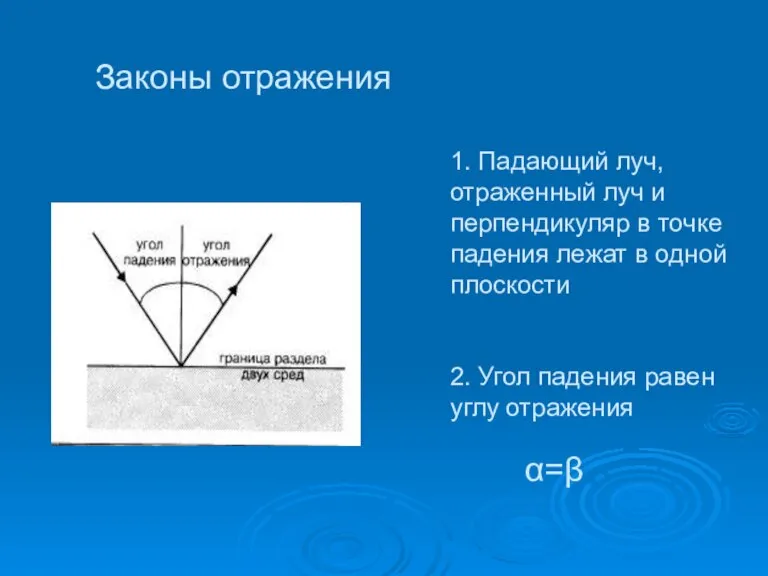
1. Падающий луч, отраженный луч и перпендикуляр в точке падения лежат в одной плоскости
2. Угол падения равен углу отражения
Законы отражения
α=β

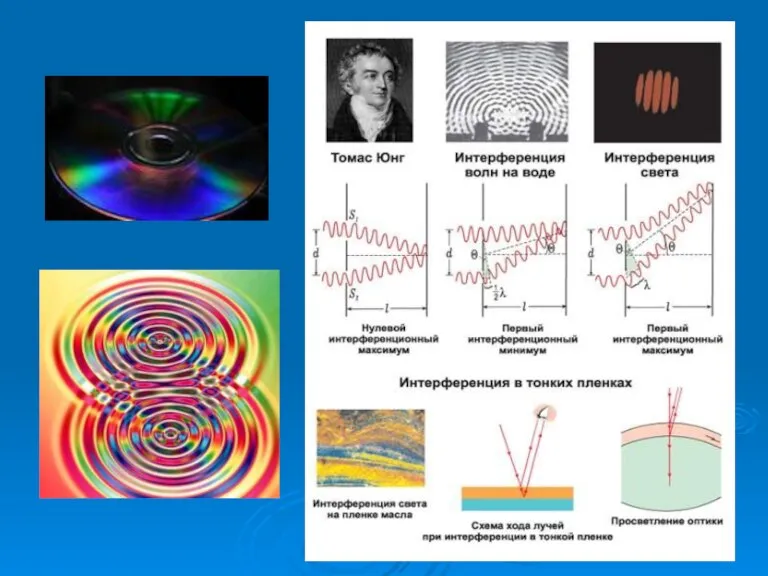
Интерференция волн
Устойчивая картина чередования максимумов и минимумов колебаний точек среды при наложении когерентных волн
Когерентные волны – это волны одинаковой частоты с постоянной разностью фаз

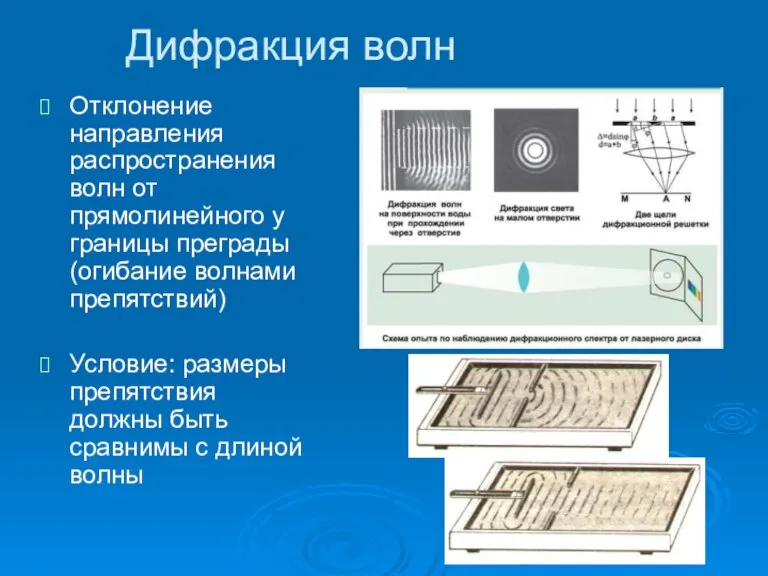
Дифракция волн
Отклонение направления распространения волн от прямолинейного у границы преграды (огибание волнами препятствий)
Условие: размеры препятствия должны быть сравнимы с длиной волны

Поляризация – это выделение колебаний поперечной волны строго одного направления (при помощи поляризатора)

2. «Благодаря» какому явлению в наших домах дребезжат стекла, когда вблизи пролетает самолет?
А) резонанс Б) дифракция В) преломление
3. Высота звука определяется
А) частотой Б) амплитудой В) длиной волны
4. Слышать друг друга в густом лесу мы можем только благодаря
эффекту
А) отражения Б) дифракции
В) преломления волн
5. Каков период на рисунке 1?
А) 20см Б) 8с В) 2м
1. Какое изображение не отражает явление интерференции волн?
А)1 Б)2 В)3
2
1
3
Тест по теме
Рис. 1