Слайд 2Основная литература
Л1. Гольдштейн Б.С. Системы коммутации. Учебник для ВУЗов. 2-е издание, доп.

и испр.//СПб.: BHV-2004.
Л2. Гольдштейн Б.С. Сигнализация в сетях связи. Том 1. 4-е издание. СПб.: BHV, 2005.
Слайд 3Изложение этого материала в:
[Л1]. Параграф 1.7
[Л2]. Параграф 2.3
![Изложение этого материала в: [Л1]. Параграф 1.7 [Л2]. Параграф 2.3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020236/slide-2.jpg)
Слайд 4
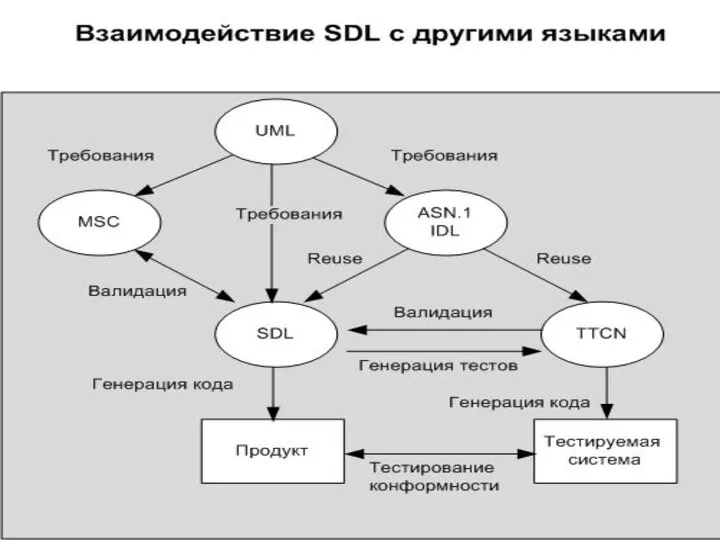
Язык описаний и спецификаций SDL.
Язык MSC (Message Sequence Chart).
Язык TTCN (Tree and

Tabular Combined Notation).
Язык ASN.1.
Слайд 6Элементы теории спецификаций ПО
Различные способы задания языков спецификаций:
Грамматики
Конечные автоматы
Спецификация должна быть конечным
Должен

существовать алгоритм, за конечное число шагов проверяющий принадлежность некоторой входной спецификации
Наиболее распространенные формализмы для задания языков: грамматики, регулярные выражения, конечные и магазинные автоматы, машины Тьюринга
Слайд 7Конечные автоматы
Конечный автомат – это пятерка
M = (Q, Σ, δ, q0, F),

где
Q – конечное множество состояний
Σ – конечное множество допустимых входных символов
δ – функция перехода
q0 из Q – начальное состояние
F – множество заключительных состояний
Слайд 8Детерминированные конечные автоматы
Автомат называется детерминированным, если множество δ(q, a) содержит не более

одного состояния для любых q, a. Если δ(q, a) всегда содержит ровно одно состояние, то автомат называется полностью определенным.
Цепочка w допускается автоматом M, если существует последовательность шагов, приводящая нас по этой цепочке в заключительное состояние автомата
Язык распознается конечным автоматом, если им распознается каждое слово языка
Удобная форма записи конечных автоматов – диаграммы переходов
Слайд 9Недетерминированные и конечные автоматы
Любому недетерминированному автомату соответствует детерминированный автомат, определяющий тот же

самый язык, причем известен метод конструирования эквивалентного конечного автомата
Таким образом, классы языков, задаваемых недетерминированными и детерминированными конечными автоматами, совпадают
Конечные автоматы – удобный формализм, так как их легко моделировать программно
Слайд 10Минимизация конечного автомата
Как найти автомат, эквивалентный данному, с минимальным числом состояний?
Алгоритм минимизации

конечного автомата выглядит так:
Вначале мы удаляем все недостижимые состояния
Затем разбиваем множество всех достижимых состояний на классы эквивалентности неразличимых состояний
Из каждого класса эквивалентности мы берем только по одному представителю
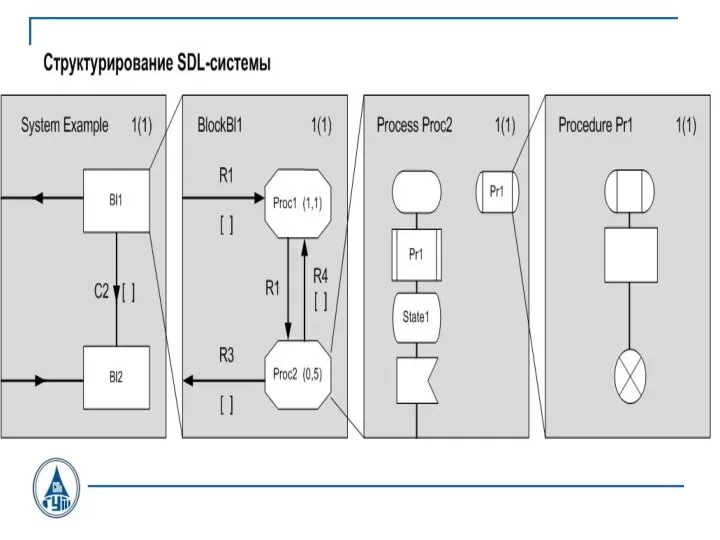
Слайд 11План:
SDL-система
SDL-блок
SDL-процесс
Синтаксис и семантика языка SDL
Примеры

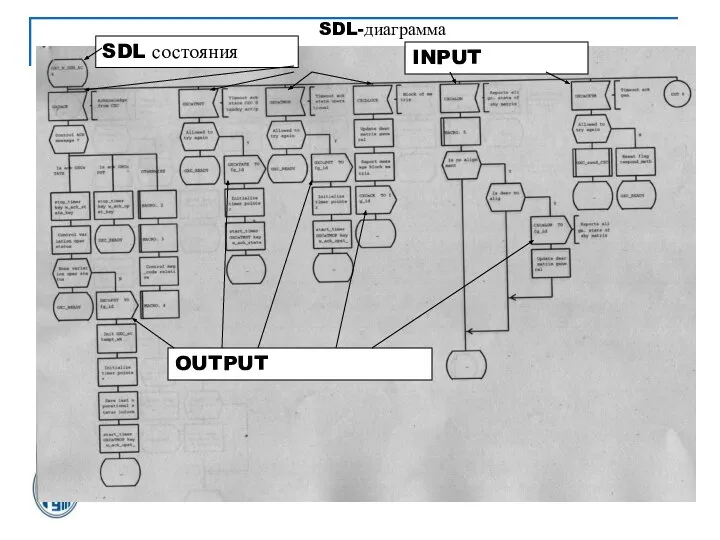
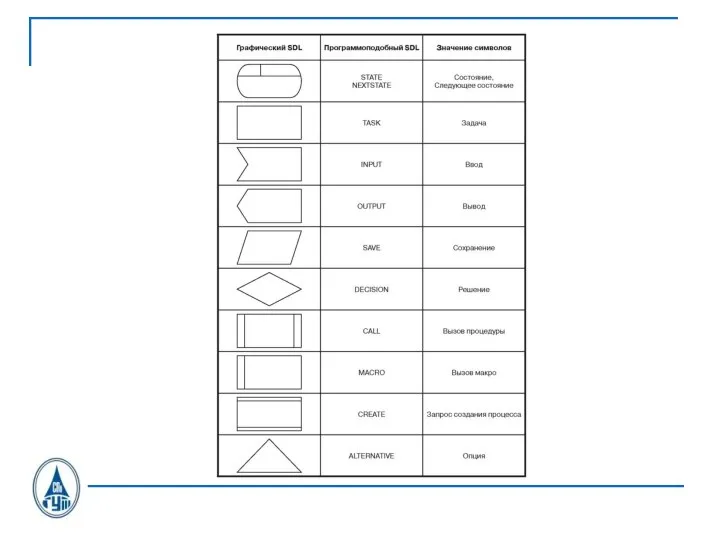
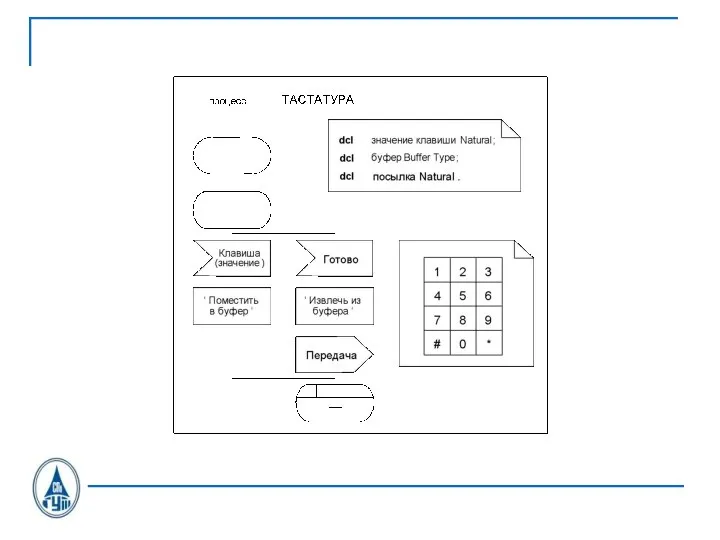
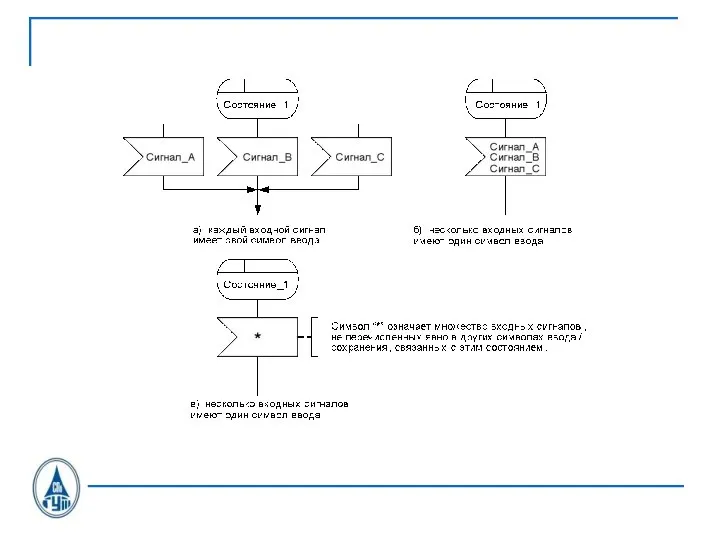
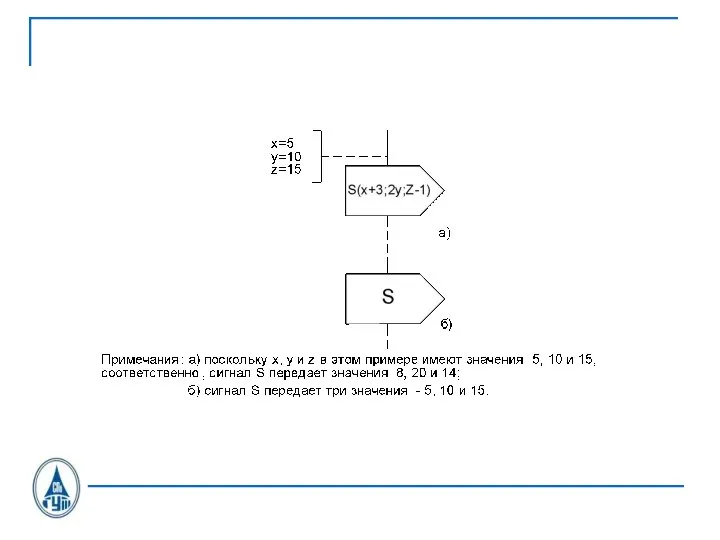
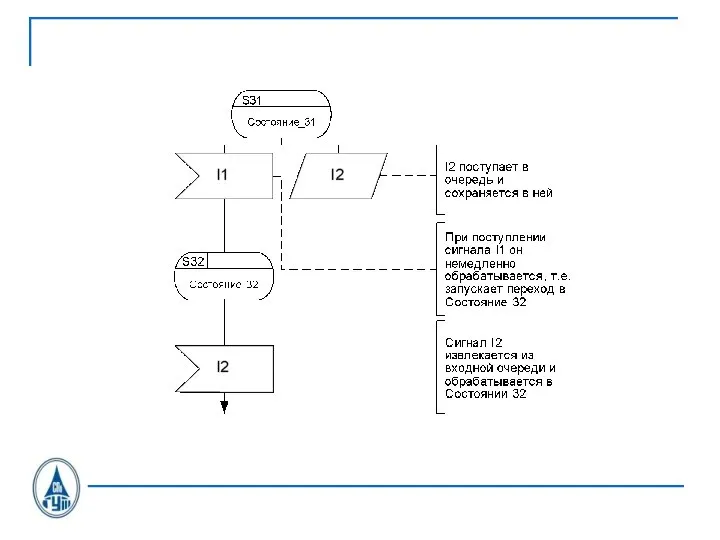
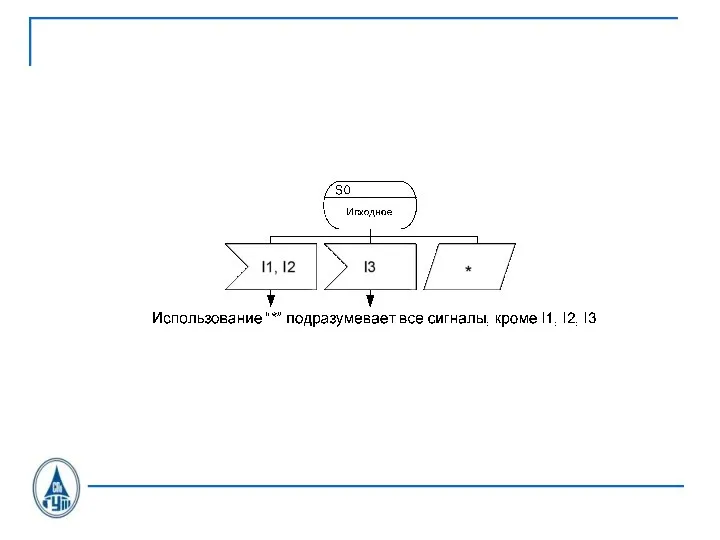
Слайд 26SDL состояния
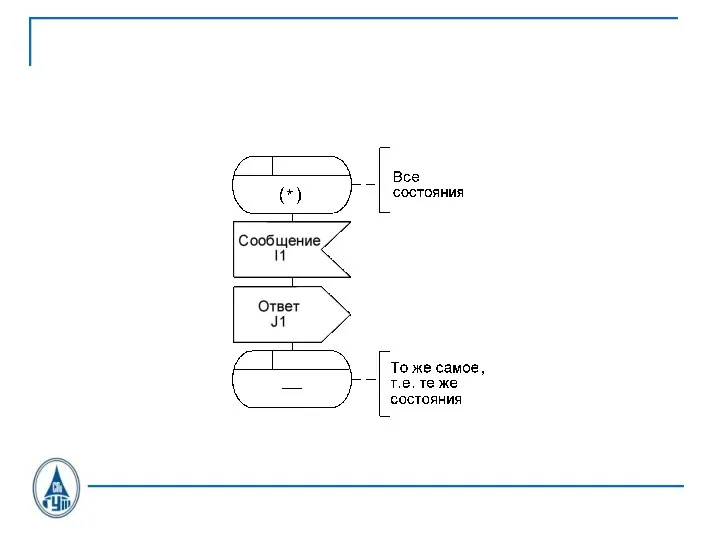
INPUT
OUTPUT
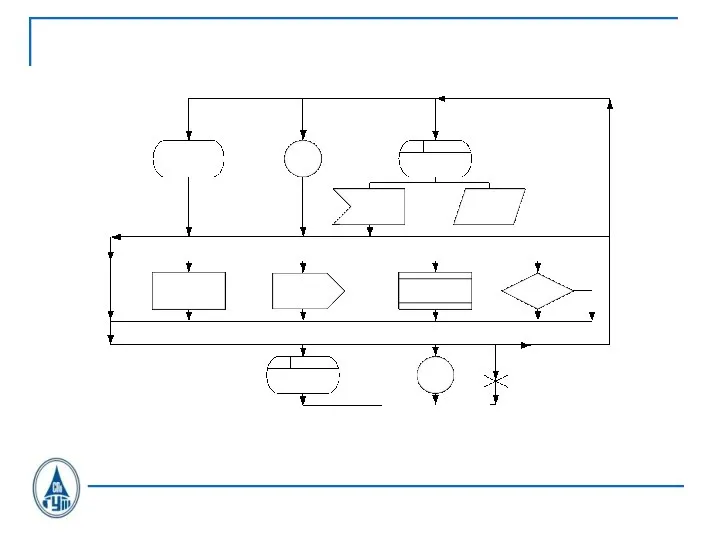
SDL-диаграмма
Слайд 32Изложение этого материала в:
[Л1]. Параграф 9.4.
[Л2]. Параграф 2.1, 2.2 и 2.3
![Изложение этого материала в: [Л1]. Параграф 9.4. [Л2]. Параграф 2.1, 2.2 и 2.3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020236/slide-31.jpg)
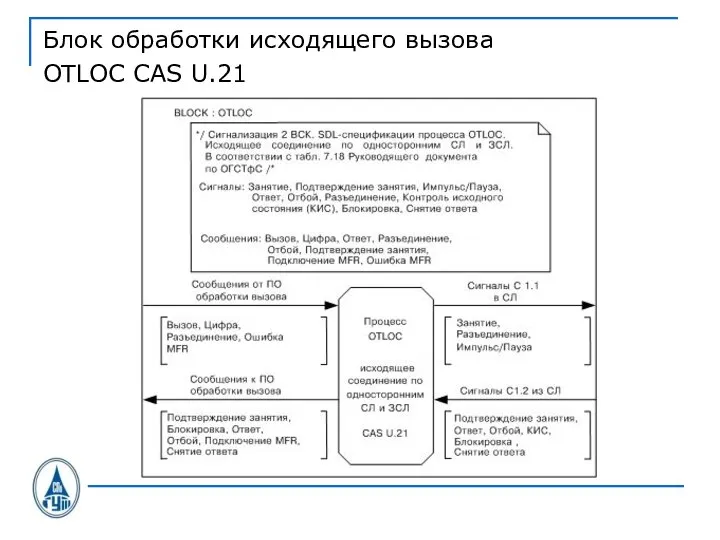
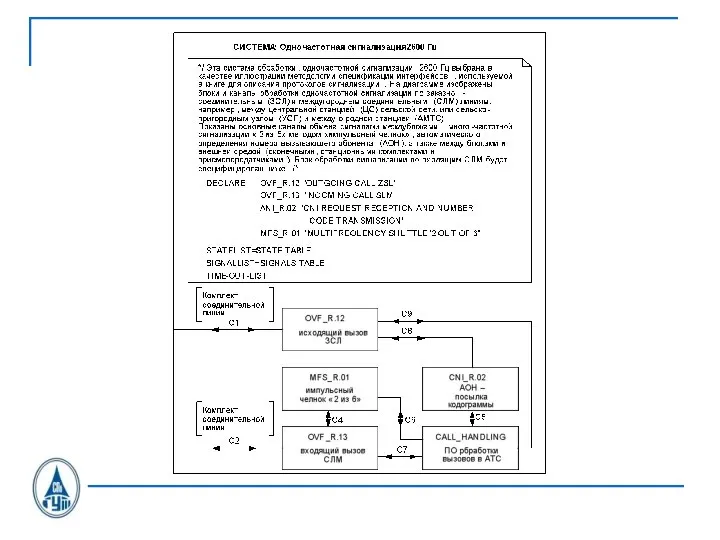
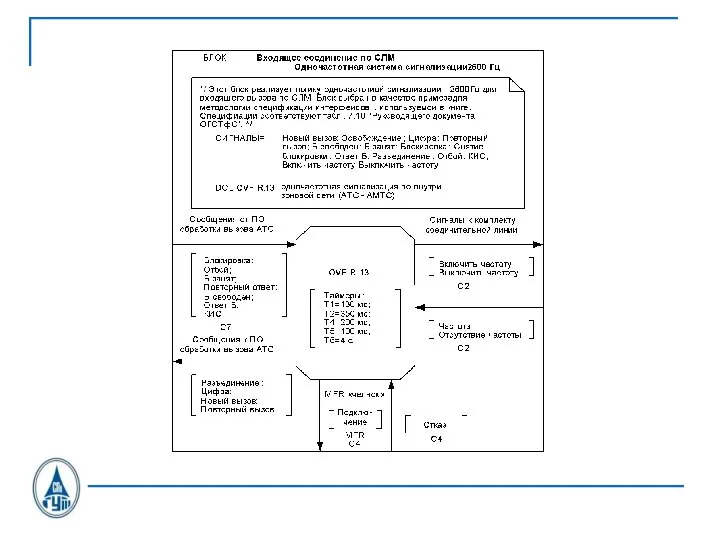
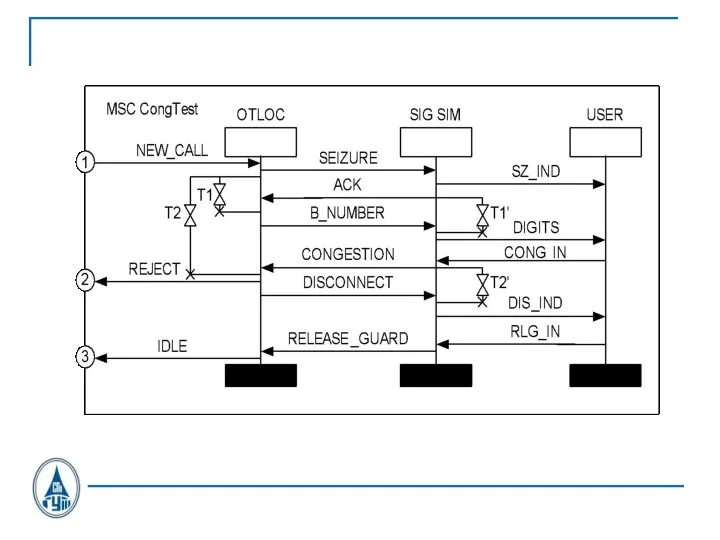
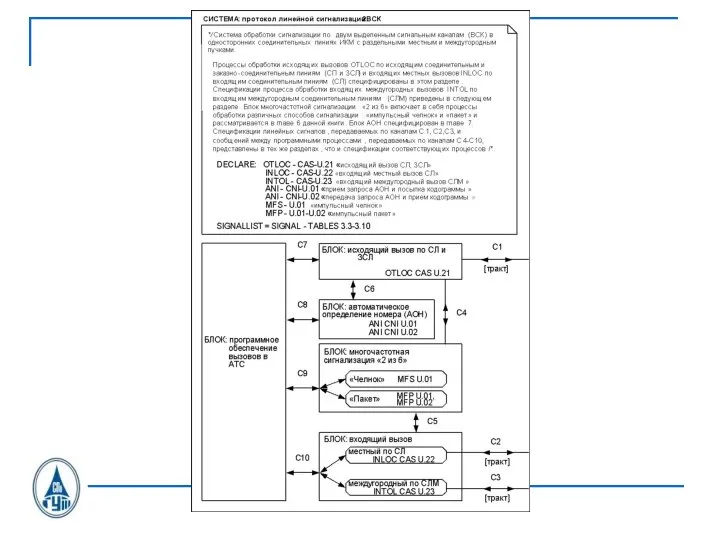
Слайд 33Блок обработки исходящего вызова
OTLOC CAS U.21
Слайд 34Сигналы С1.1, передаваемые в сторону линейного тракта от процесса OTLOC при исходящем
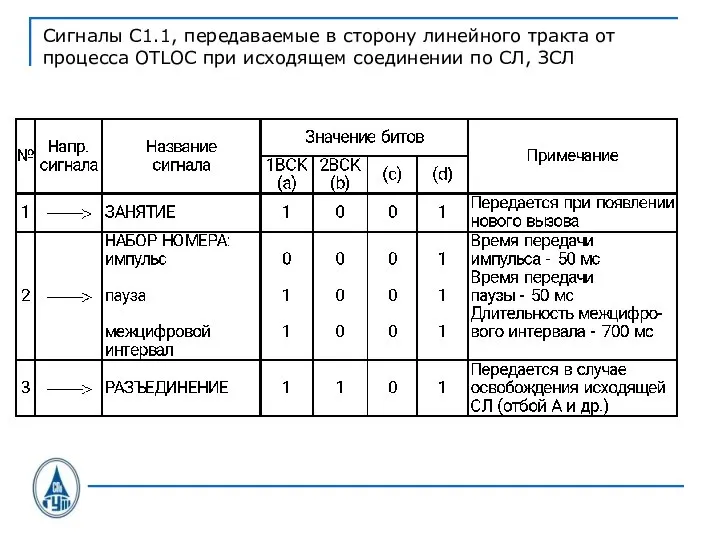
соединении по СЛ, ЗСЛ
Слайд 35Сигналы С1.2, принимаемые в OTLOC со стороны линейного тракта при исходящем соединении
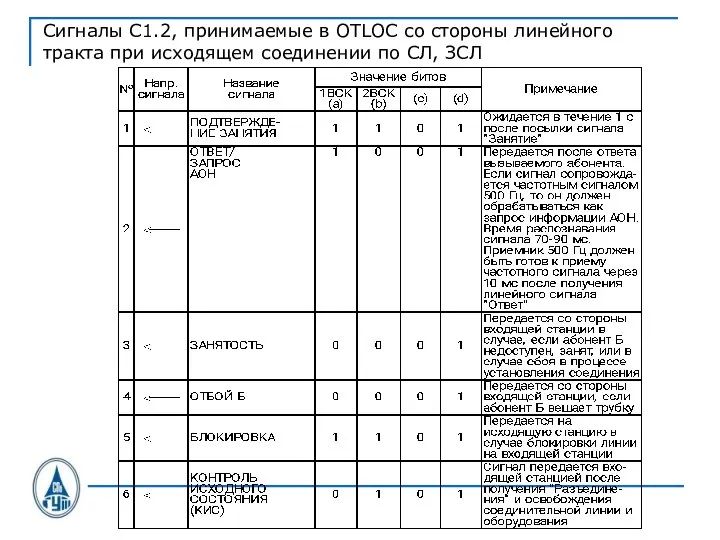
по СЛ, ЗСЛ
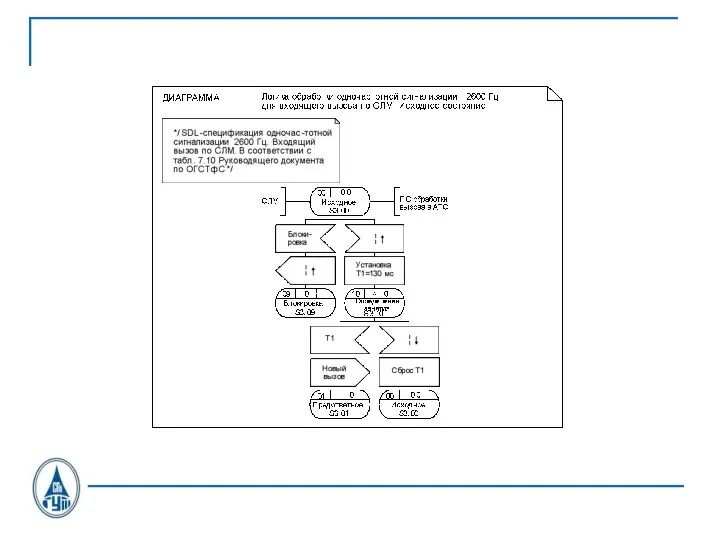
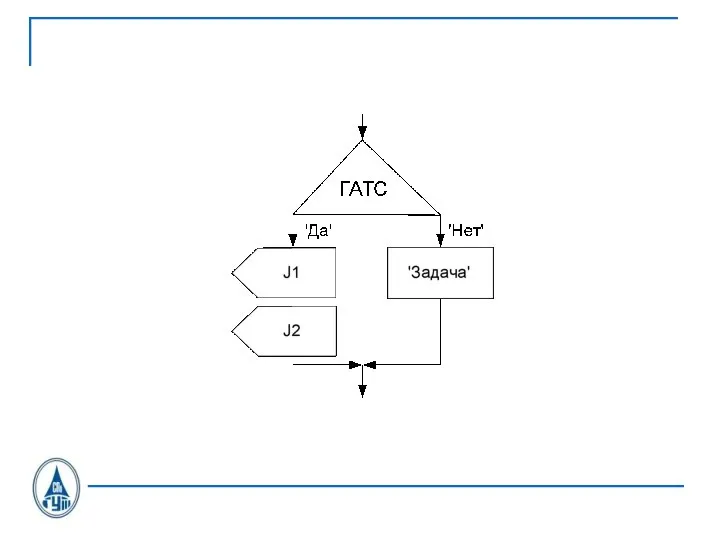
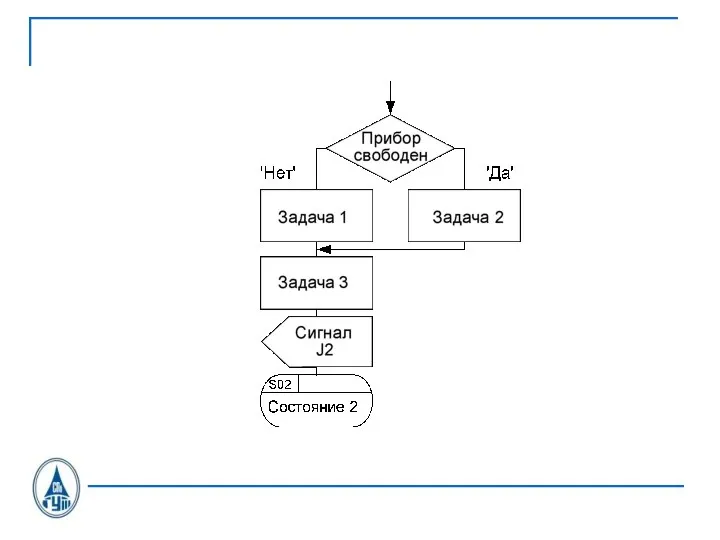
Слайд 36SDL-диаграмма процесса OTLOC CAS U.21
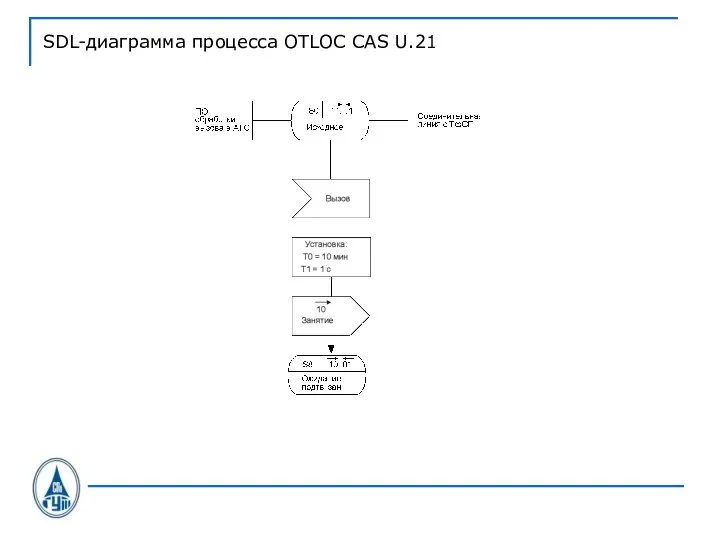
Слайд 37SDL-диаграмма процесса OTLOC CAS U.21
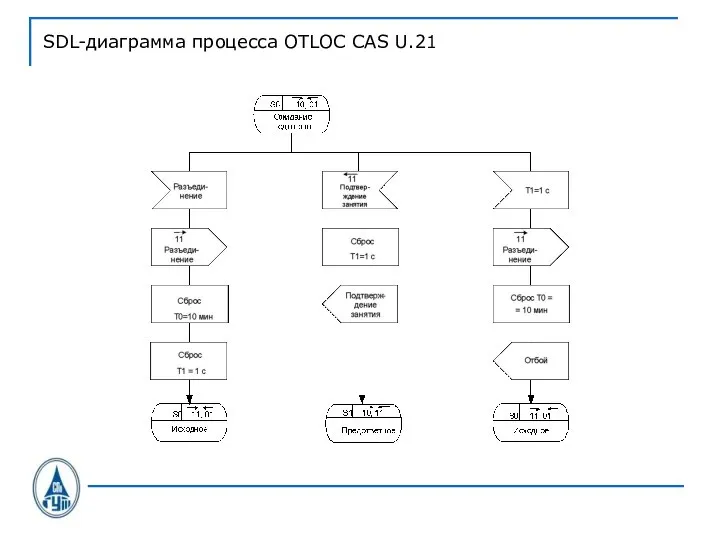
Слайд 38SDL-диаграмма процесса OTLOC CAS U.21
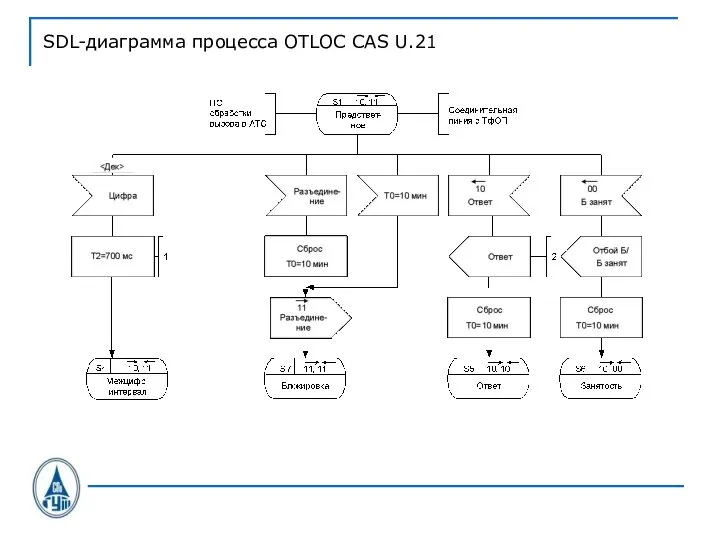
Слайд 39SDL-диаграмма процесса OTLOC CAS U.21
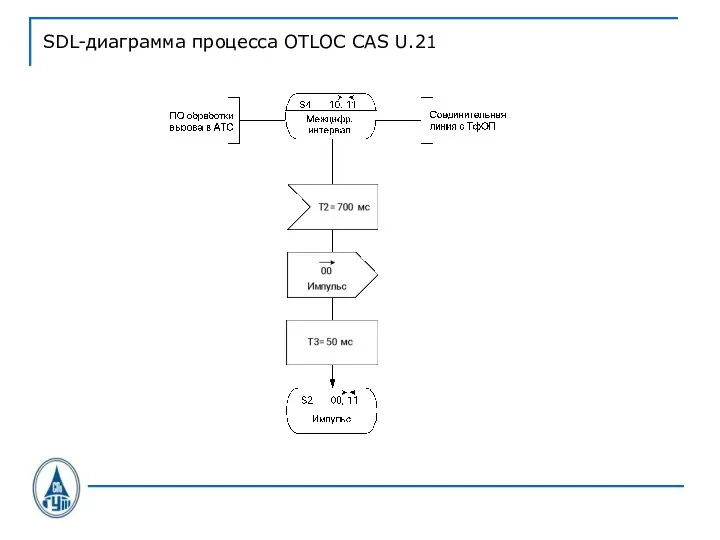
Слайд 40SDL-диаграмма процесса OTLOC CAS U.21
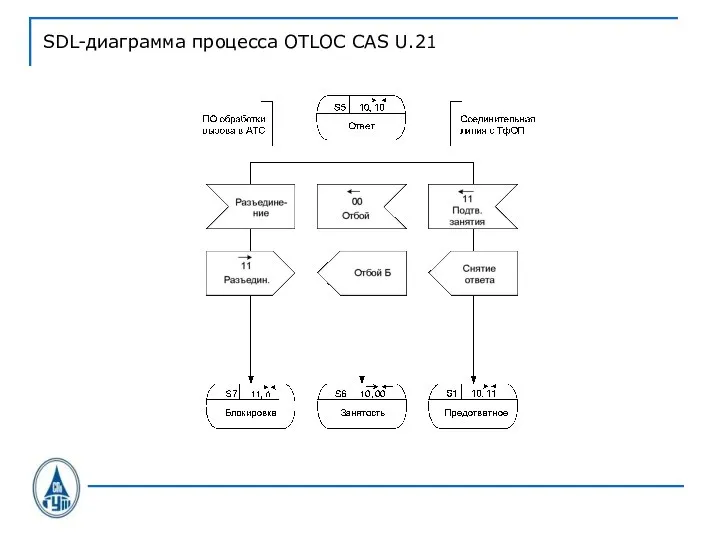
Слайд 41SDL-диаграмма процесса OTLOC CAS U.21
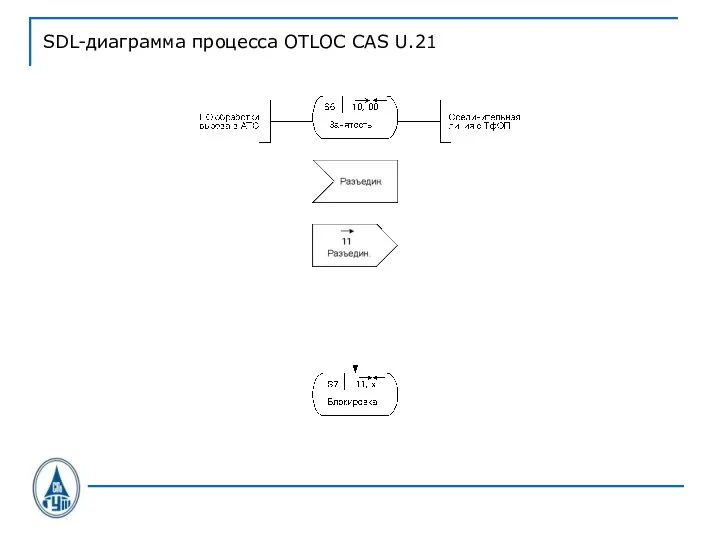
Слайд 42SDL-диаграмма процесса OTLOC CAS U.21
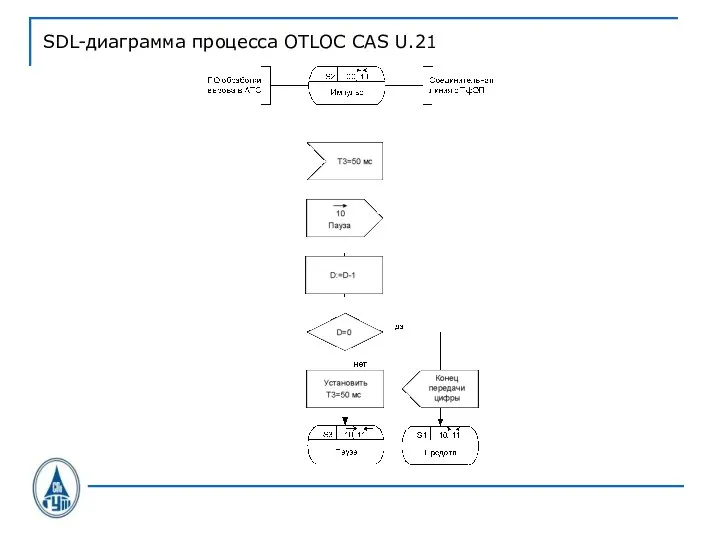
Слайд 43SDL-диаграмма процесса OTLOC CAS U.21
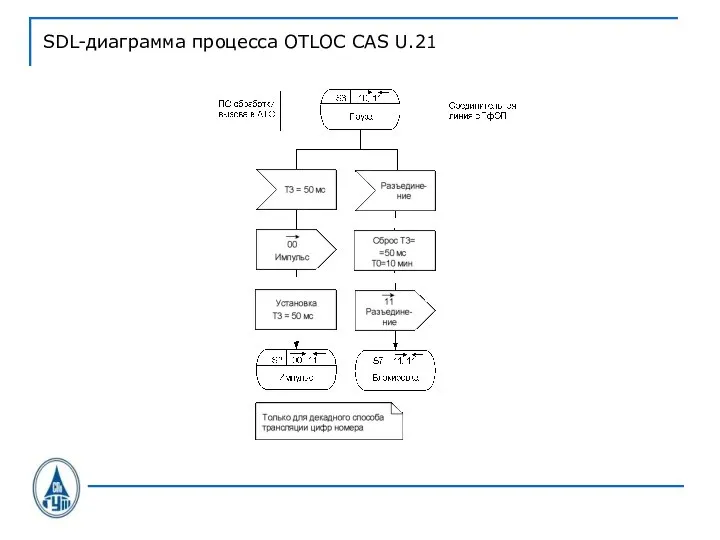
Слайд 44SDL-диаграмма процесса OTLOC CAS U.21
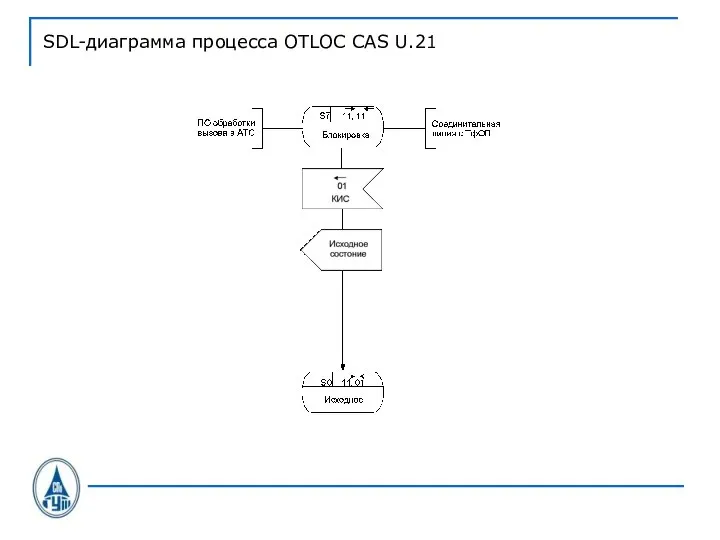
Слайд 45Изложение этого материала в:
[Л1]. Параграф 8.2
[Л2]. Параграф 3.2
![Изложение этого материала в: [Л1]. Параграф 8.2 [Л2]. Параграф 3.2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020236/slide-44.jpg)

![Изложение этого материала в: [Л1]. Параграф 1.7 [Л2]. Параграф 2.3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020236/slide-2.jpg)








![Изложение этого материала в: [Л1]. Параграф 9.4. [Л2]. Параграф 2.1, 2.2 и 2.3](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020236/slide-31.jpg)












![Изложение этого материала в: [Л1]. Параграф 8.2 [Л2]. Параграф 3.2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1020236/slide-44.jpg)
 Дифференциальная диагностика нейроинфекций
Дифференциальная диагностика нейроинфекций Формы записи алгоритмов
Формы записи алгоритмов В зоопарке
В зоопарке Суффиксы
Суффиксы «Создание сообщества для разработки и реализации системы дистанционной диагностики»
«Создание сообщества для разработки и реализации системы дистанционной диагностики» ИТОГИ РАЗВИТИЯ ЭКОНОМИКИ И СОЦИАЛЬНОЙ СФЕРЫ КЕМЕРОВСКОЙ ОБЛАСТИ В 2008 ГОДУ
ИТОГИ РАЗВИТИЯ ЭКОНОМИКИ И СОЦИАЛЬНОЙ СФЕРЫ КЕМЕРОВСКОЙ ОБЛАСТИ В 2008 ГОДУ Описание уровней развития отношения ребенка к той или иной ценности.Это - не точный диагноз, это – тенденция, повод для Вашего пед
Описание уровней развития отношения ребенка к той или иной ценности.Это - не точный диагноз, это – тенденция, повод для Вашего пед кроссворд1
кроссворд1 Телерадиожурналистика
Телерадиожурналистика О Б Р А З И В А Н У Ш К И - Д У Р А Ч К А
О Б Р А З И В А Н У Ш К И - Д У Р А Ч К А Лубочные картинки как первые комиксы
Лубочные картинки как первые комиксы Финансовый рынок
Финансовый рынок Презентация на тему Электробезопасность Опасности электрических систем
Презентация на тему Электробезопасность Опасности электрических систем  Диалог-форум «Долгосрочное накопительное страхование в России»О проекте Стратегии развития страхового рынка до 2020 года. Пробле
Диалог-форум «Долгосрочное накопительное страхование в России»О проекте Стратегии развития страхового рынка до 2020 года. Пробле Дмитрий Иванович Менделеев (1834–1907)
Дмитрий Иванович Менделеев (1834–1907) Исследовательский проект на тему:
Исследовательский проект на тему: Художник и ученый
Художник и ученый Роль преподавателя в повышении качества обучения в условиях дистанционного образования
Роль преподавателя в повышении качества обучения в условиях дистанционного образования Нарушения родовой деятельности
Нарушения родовой деятельности Собственные имена
Собственные имена СЮРВЕЙ И СТРАХОВАНИЕ
СЮРВЕЙ И СТРАХОВАНИЕ Анализ. Контекст. Постановка исследовательского вопроса
Анализ. Контекст. Постановка исследовательского вопроса Презентация на тему Битва на Чудском озере
Презентация на тему Битва на Чудском озере  Путешествие по Солнечной системе
Путешествие по Солнечной системе Школьная жизнь в фактах и цифрах
Школьная жизнь в фактах и цифрах Сленгізм дерибанити в українському медіаполітичному дискурсі: семантико-дистрибутивний аналіз
Сленгізм дерибанити в українському медіаполітичному дискурсі: семантико-дистрибутивний аналіз Маршрутная сеть автобусов
Маршрутная сеть автобусов Презентация на тему Источники света. Распространение света
Презентация на тему Источники света. Распространение света