Содержание
- 2. Краткое содержание 1. Введение 2. История 3. Сетевая модель 4. Сети, поддерживающие эффективный поиск 5. Выводы
- 3. Введение “Мир тесен” тема анекдотических исследований и фольклора часто бывает, что мы встречаем незнакомца и оказывается,
- 4. задача поиска информации поведение пользователей Web поведение агентов поисковые протоколы (Gnutella, Freenet) Введение(2)
- 5. Эксперимент Стэнли Милграма проведенный в 1960х, остается одним из самых удачных в понимании проблемы человек из
- 6. короткие пути в сетях знакомств существуют люди могут находить эти пути, зная только информацию о конечной
- 7. Исследования Пула и Кочена случайные сети имеют маленький диаметр если А и Б два индивидуума с
- 8. Модель Ватса и Строгатца балансирует между ограничениями разветвленности сети знакомств и диаметра сети пример - «сетчатый
- 9. Исследования Джона Клайнберга Почему незнакомые люди могут найти, соединяющую их короткую цепь знакомств? Существуют скрытые навигационные
- 10. Открытия Джона Клайнберга существующих моделей недостаточно, чтобы объяснить успех децентрализованного алгоритма для одной из моделей класса
- 11. Другие работы по теме как индивидуумы выбирают следующего адресата Бернард и Килворф : «обратные эксперименты тесного
- 12. Сетевая модель Описание модели Децентрализованные алгоритмы Результаты применения модели k – мерная сеть
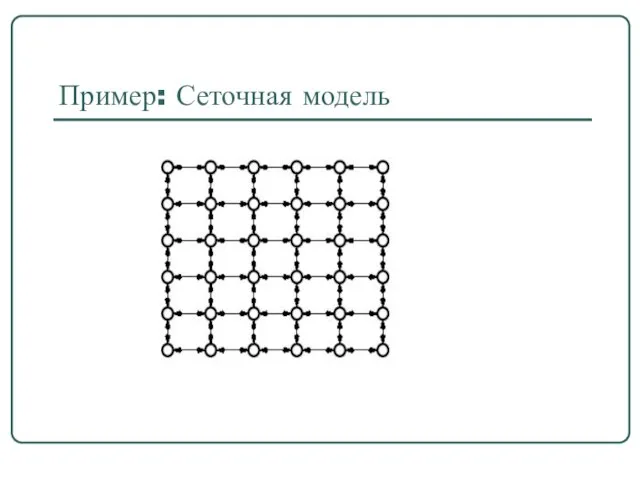
- 13. Описание модели квадратная сетка n × n , {(i; j) : i ∈ {1; 2; :
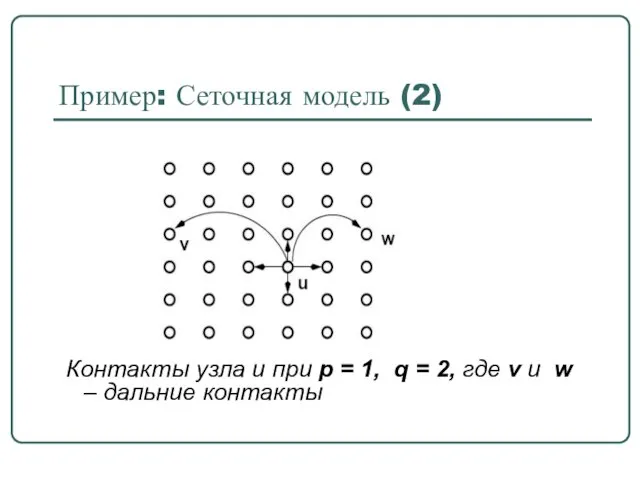
- 14. Описание модели(2) p >= 1 - локальные контакты q >= 0 - удаленные контакты r >=
- 15. Пример: Сеточная модель
- 16. Контакты узла u при p = 1, q = 2, где v и w – дальние
- 17. считая p и q фиксированными константами получаем однопараметрическое семейство сетей, зависящее от показателя r r –
- 18. Децентрализованные алгоритмы На каждом шаге держатель сообщения знает: множество локальных контактов местоположение цели на решетке *
- 19. Децентрализованные алгоритмы Ожидаемое время доставки ожидаемое количество шагов по пути порождаем граф в соответствии с обратным
- 20. Результаты применения модели Теорема 1: Существует константа a0, зависящая от p и q, не зависящая от
- 21. Теорема 2: Существует децентрализованный алгоритм А и константа a2, независящая от n, так что при r
- 22. Фундаментальное следствие когда дальние контакты создаются процессом, связывающих их определенным образом с геометрией решетки поиск эффективен
- 23. Главные предположения теорем В первой теореме равномерное распределение не позволяет алгоритму использовать скрытые «ключи» геометрии решетки
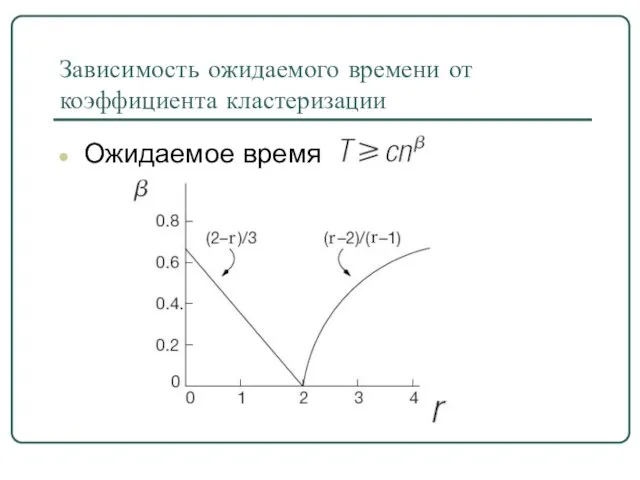
- 24. 0 Существует константа ar, зависящая от p, q, r, независимая от n, такая что ожидаемое время
- 25. Зависимость ожидаемого времени от коэффициента кластеризации Ожидаемое время
- 26. k - мерная сеть обобщение результатов алгоритм может строить пути с длиной, полиноминально зависящей от log
- 27. Скорость передачи «скорость передачи» класса сетей минимизация диаметра не то же самое что минимизация ожидаемого времения
- 28. Сети, поддерживающие эффективный поиск Иерархическая сетевая модель Модель с полилогарифмическим внешним уровнем Модель с постоянным внешним
- 29. Иерархическая сетевая модель b - арное дерево T, b = const V – набор листьев из
- 30. k = c log2n, где с = const растет асимптотически как Модель с полилогарифмическим внешним уровнем
- 31. Естественные интерпретации модели WWW иерархия тем (yahoo.com) Science/Computer_Science/Algorithms более вероятно будет связана с Science/Computer_Science/Machine_Learning, чем с
- 32. Полученные результаты Теорема ∃ иерархическая модель степени α = 1 с полилогарифмическим внешним уровнем, у которой
- 33. Полученные результаты Теорема(продолжение) ∀ α ≠ 1, не существует иерархической модели степени α с полилогарифмическим внешним
- 34. Групповые структуры набор узлов V собрание подмножеств V константы λ 1: R - группа размером q>=
- 35. (V, {Ri}) q(v, w) - размер наименьшей подгруппы f (⋅) – монотонная, невозрастающая f (⋅) растет
- 36. Полученные результаты Теорема: Для каждой групповой структуры существует индуцированная групповая модель степени α = 1 с
- 37. Выводы соотношение между локальной структурой и дальними контактами вблизи критического порога – появляются «ключи» сети. ниже
- 38. Открытые вопросы Вопрос Фрагно Какие из развивающихся процессов могут сделать поиск по сетям более эффективным? Осознанность
- 39. Ссылки J. Kleinberg. Navigation in a Small World. Nature 406 (2000) J. Kleinberg. The small-world phenomenon:
- 40. Ссылки(2) J. Kleinberg, P.Raghavan. Query Incentive Networks. Proc 46 th IEEE Symposium of Foundations of Computer
- 42. Скачать презентацию




































 Стандарт cXML в корпоративных приложениях электронной коммерции
Стандарт cXML в корпоративных приложениях электронной коммерции Целл-у-лосс - новинка от Herbalife. Деликатное выведение лишней жидкости из организма
Целл-у-лосс - новинка от Herbalife. Деликатное выведение лишней жидкости из организма Улица Горьковская д. 63. Планируемые мероприятия
Улица Горьковская д. 63. Планируемые мероприятия Организация аварийно-спасательных работ
Организация аварийно-спасательных работ Знаток правил дорожного движения Знаток правил дорожного движения Юсупова Ирина Равиловна МОУ «СОШ 60», г. Набережные Челны.
Знаток правил дорожного движения Знаток правил дорожного движения Юсупова Ирина Равиловна МОУ «СОШ 60», г. Набережные Челны. Контроль якості металів і зварних з'єднань
Контроль якості металів і зварних з'єднань C новым учебным годом!!! 2012/13
C новым учебным годом!!! 2012/13 Презентация на тему Физика твердого тела Кристаллофизика
Презентация на тему Физика твердого тела Кристаллофизика
 посвящение в читатели
посвящение в читатели Строим домик из спичек
Строим домик из спичек Дню Защитника Отечества посвящается
Дню Защитника Отечества посвящается Изобразительность в музыке
Изобразительность в музыке SWOT-анализ
SWOT-анализ Народное прикладное искусство
Народное прикладное искусство Творчы праэкт Humanities Blues
Творчы праэкт Humanities Blues Рудольф Арнхейм
Рудольф Арнхейм Пэчворк
Пэчворк Особенности психологического сопровождения детей с ограниченными возможностями здоровья в условиях ДОУ
Особенности психологического сопровождения детей с ограниченными возможностями здоровья в условиях ДОУ Золотое сечение на Новгородчине
Золотое сечение на Новгородчине 家人
家人 Внешняя политика СССР в 1985-1991 гг
Внешняя политика СССР в 1985-1991 гг Жилищное право
Жилищное право Презентация на тему Социальная сфера презентация
Презентация на тему Социальная сфера презентация Экслибрис. Задание по прикладной композиции
Экслибрис. Задание по прикладной композиции Итоги интернет-урока«LEARNING MORE ABOUT LONDON / УЗНАЕМ БОЛЬШЕ О ЛОНДОНЕ»
Итоги интернет-урока«LEARNING MORE ABOUT LONDON / УЗНАЕМ БОЛЬШЕ О ЛОНДОНЕ» Хить Александр АнатольевичГенеральный директор ООО "Ассистанская компания"Украинская служба помощи" тел. 8 067 630 70 88 e-mail:
Хить Александр АнатольевичГенеральный директор ООО "Ассистанская компания"Украинская служба помощи" тел. 8 067 630 70 88 e-mail:  Олимпийское движение в России
Олимпийское движение в России Мышление. Тест Какой у вас тип мышления
Мышление. Тест Какой у вас тип мышления