Многогранники

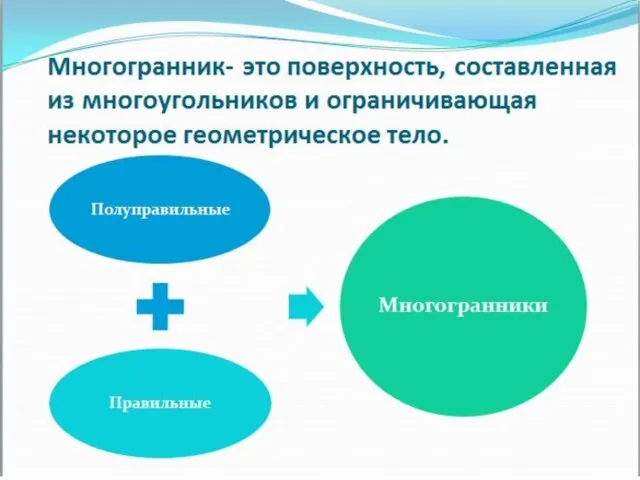
Правильный многогранник или платоновое тело — это выпуклый многогранник с максимально возможной симметрией.
Многогранник называется правильным, если:
-он выпуклый;
-все его грани являются равными правильными многоугольниками;
-в каждой его вершине сходится одинаковое число рёбер.

Платоновыми телами называются правильные однородные выпуклые многогранники, то есть выпуклые многогранники, все грани и углы которых равны, причем грани - правильные многоугольники.
Платоновы тела - трехмерный аналог плоских правильных многоугольников. Однако между двумерным и трехмерным случаями есть важное отличие: существует бесконечно много различных правильных многоугольников, но лишь пять различных правильных многогранников.
Доказательство этого факта известно уже более двух тысяч лет; этим доказательством и изучением пяти правильных тел завершаются "Начала" Евклида.
Платон
около 428 – 347 гг до н.э.

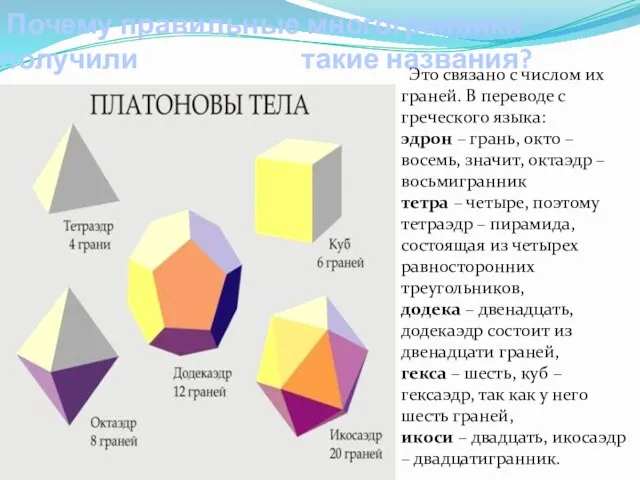
Почему правильные многогранники получили такие названия?
Это связано с числом их граней. В переводе с греческого языка:
эдрон – грань, окто – восемь, значит, октаэдр – восьмигранник
тетра – четыре, поэтому тетраэдр – пирамида, состоящая из четырех равносторонних треугольников,
додека – двенадцать, додекаэдр состоит из двенадцати граней,
гекса – шесть, куб – гексаэдр, так как у него шесть граней,
икоси – двадцать, икосаэдр – двадцатигранник.

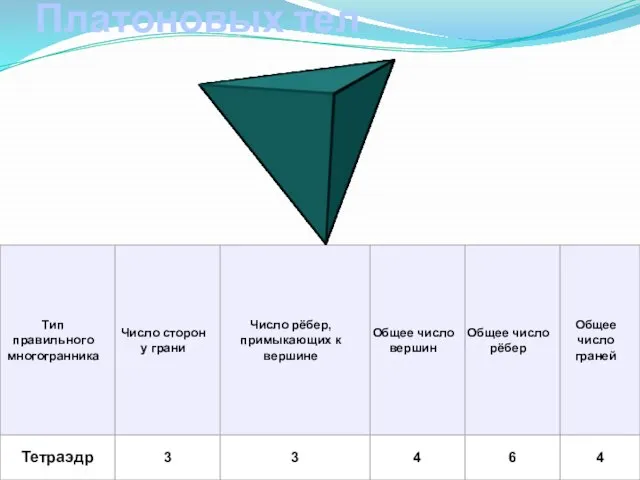
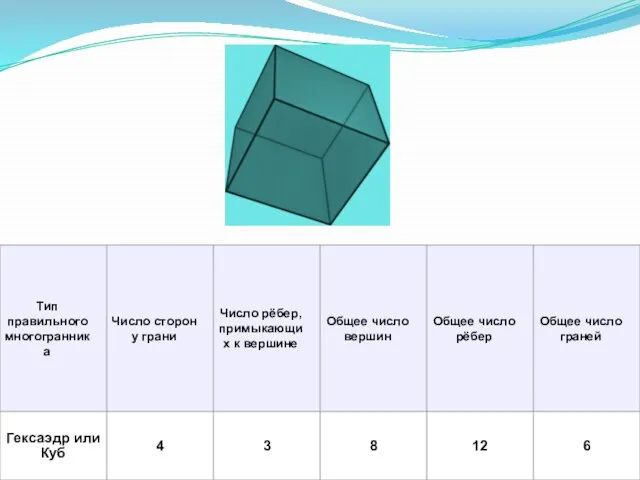
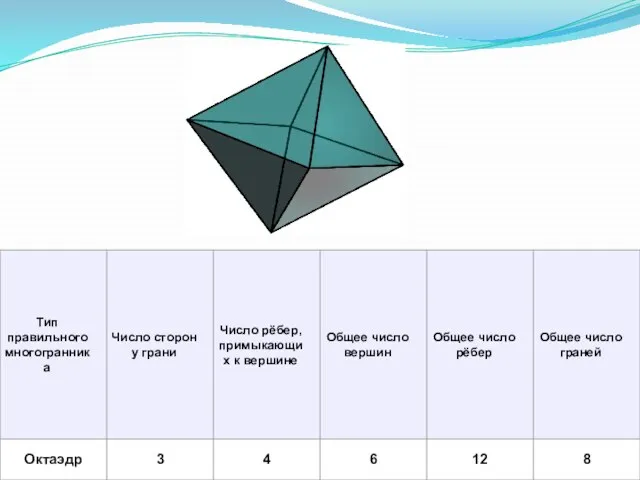
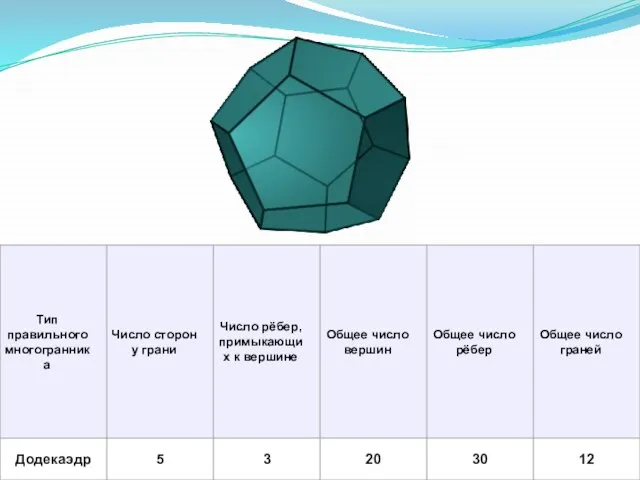
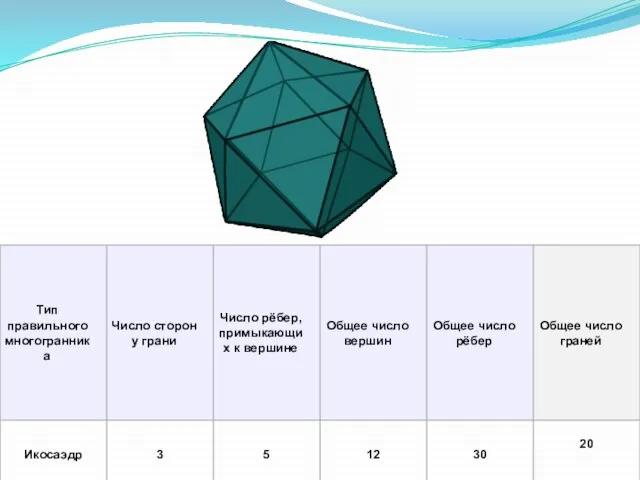
Характеристика Платоновых тел

Полуправильные многогранники - определение может варьироваться и включать различные типы многогранников, но в первую очередь сюда относятся архимедовы тела.
Архимедовы тела — выпуклые многогранники, обладающие двумя свойствами:
Все грани являются правильными многоугольниками двух или более типов (если все грани — правильные многоугольники одного типа, это — правильный многогранник);
Для любой пары вершин существует симметрия многогранника (то есть движение переводящее многогранник в себя) переводящая одну вершину в другую. В частности,
Все многогранные углы при вершинах конгруэнтны.
Полуправильные многогранники

Множество Архимедовых тел можно разбить на пять групп.
Первую из них составляют пять многогранников, которые получаются из Платоновых тел в результате их усечения.
УСЕЧЕННЫЙ КУБ

УСЕЧЕННЫЙ ИКОСАЭДР

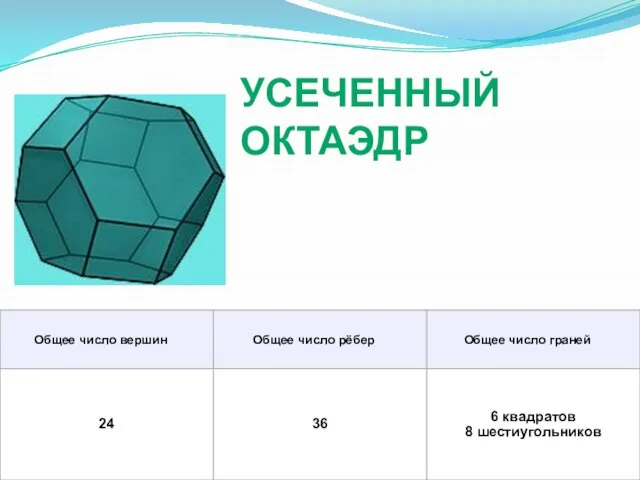
УСЕЧЕННЫЙ ОКТАЭДР

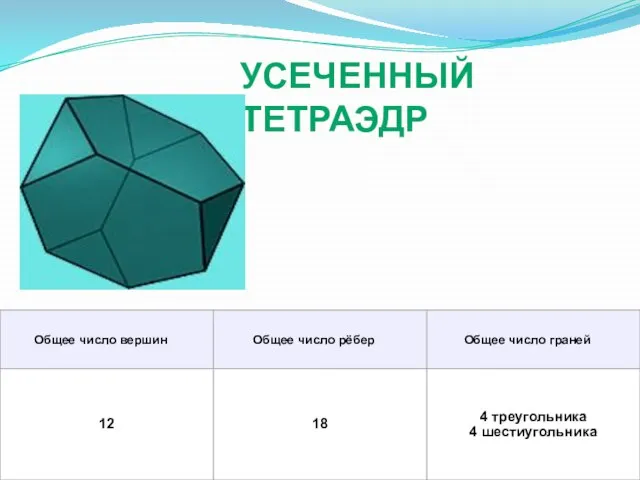
УСЕЧЕННЫЙ ТЕТРАЭДР

УСЕЧЕННЫЙ ДОДЕКАЭДР

Вторую группу Архимедовых тел составляют два тела, именуемых квазиправильными многогранниками.
КУБООКТАЭДР

ИКОСОДОДЕКАЭДР

Третья группа Архимедовых тел, в нее входят:
РОМБОКУБООКТАЭДР

РОМБОИКОСОДОДЭКАЭДР

Четвертая группа Архимедовых тел:
КУРНОСЫЙ КУБ

КУРНОСЫЙ ДОДЕКАЭДР

Пятая группа Архимедовых тел состоит из одного многогранника:
ПСЕВДОРОМБОКУБООКТАЭДР

Также существуют звёздчатые многогранники
Звёздчатый многогранник (звёздчатое тело) — это невыпуклый многогранник, грани которого пересекаются между собой. Как и у незвёздчатых многогранников грани попарно соединяются в ребрах, при этом внутренние линии пересечения не считаются рёбрами.
Звёздчатой формой многогранника называется многогранник, полученный путём продления граней данного многогранника через рёбра до их следующего пересечения с другими гранями по новым рёбрам.
Правильные звёздчатые многогранники - это звёздчатые многогранники, гранями которых являются одинаковые правильные или звёздчатые многоугольники. Существует всего 4 правильных звёздчатых тела, не являющиеся соединениями платоновых и звёздчатых тел, называемые телами Кепплера-Пуансо.

1. ЗВЁЗДЧАТЫЙ ОКТАЭДР
2.ЗВЁЗДЧАТЫЕ ФОРМЫ ДОДЕКАЭДРА

3.ЗВЁЗДЧАТАЯ ФОРМА ИКОСАЭДРА

4.ЗВЁЗДЧАТАЯ ФОРМА КУБООКТАЭДРА
5.ЗВЁЗДЧАТАЯ ФОРМА ИКОСОДОДЕКАЭДРА