МНОГОМАСШТАБНЫЕ ИНТЕГРАЛЬНЫЕ ТРАНСФОРМАЦИИ В СВЕТЕ ИХ ПРИМЕНЕИЯ К РЕШЕНИЮ НЕКОТОРЫХ ЗАДАЧ ГЕОФИЗИКИ

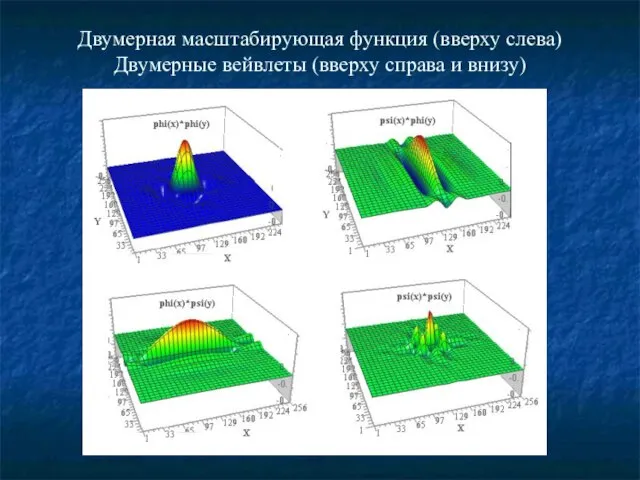
Одномерные вейвлеты оперируют двумя основными параметрами:
масштабом (scale) и
положением (location).
Двумерные вейвлеты, кроме того, имеют фиксированное количество направлений, по которым они имеют повышенную чувствительность в процессе анализа многомерных данных. Но в реальных сигналах могут присутствовать совершенно другие направления, которые нужно подчеркнуть посредством трансформации данных. В последнее десятилетие появилось большое число публикаций, посвященных классу трансформаций многомерных данных, которые включают дополнительный параметр – ориентацию линейных сегментов. Наряду с алгоритмами многомасштабного анализа сигналов, индуцированными вейвлетами, этот класс интегральных трансформаций пронизывают идеи, содержащиеся в преобразовании Радона, – математическом аппарате, лежащем в основе компьютерной томографии. В отличии от вейвлетов, трансформации, о которых здесь пойдет речь, в число основных параметров включают три элемента:
масштаб (scale),
положение (location) ,
ориентацию (orientation) линейных сегментов данных.

Список основных интегральных трансформаций данных на основе многомасштабного анализа
Приведем перечень основных модификаций интегральных преобразований рассматриваемого класса:
beamlet transform (бимлет-преобразование),
curvelet transform (курвлет-преобразование),
ridgelet transform (риджлет-преобразование).
Эти и подобные им трансформация двумерных и многомерных данных обладают высокой чувствительностью и точностью при обнаружении и выделении объектов и их границ. Для краткости иногда будем называть их одним именем
бимлет-преобразования.
---------------------------------------------------------------
Основные ссылки делаются на сайты в Интернете.
Beam – луч, beamlet – маленький луч, лучик, штрих, отрезок

Фильтрация данных
Алгоритмы фильтрации данных основаны на выборе порога во множестве коэффициентов интегральных преобразований, посредством которого часть коэффициентов заменяется нулями (процедура Thresholding). После этого выполняется реконструкция данных посредством соответствующего обратного преобразования. Выбор оптимального порога является достаточно сложной математической задачей. По этой теме имеется рад интересных публикаций. Она нашла удовлетворительное решение при сжатии данных и борьбы с шумом посредством вейвлет-анализа. Некоторую информацию по проблеме можно найти в книгах [Дьяконов, 2004; Смоленцев, 2005] и описании алгоритмов программ Wavelet Toolbox СКМ MATLAB.

Непрерывное одномерное вейвлет-преобразование
Пусть фиксирована функция , имеющая нулевое интегральное среднее
и достаточно быстро стремящаяся к нулю при . Назовем ее вейвлетом или всплеском. На основе вейвлета путем сдвигов и изменения масштаба построим функцию
в которой – параметр масштаба, – параметр сдвига.
Прямое и обратное преобразование

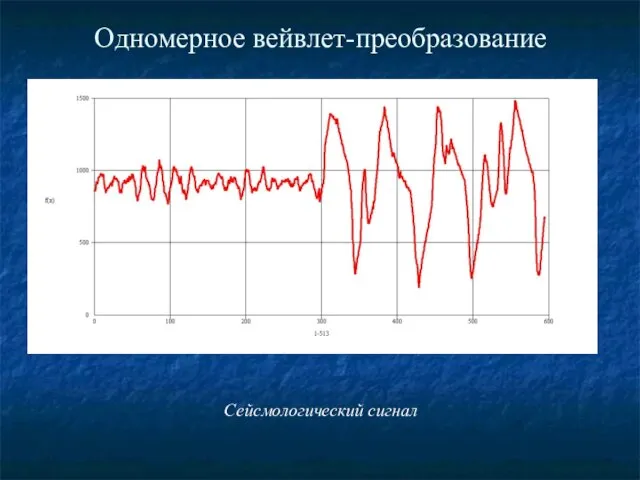
Одномерное вейвлет-преобразование
Сейсмологический сигнал

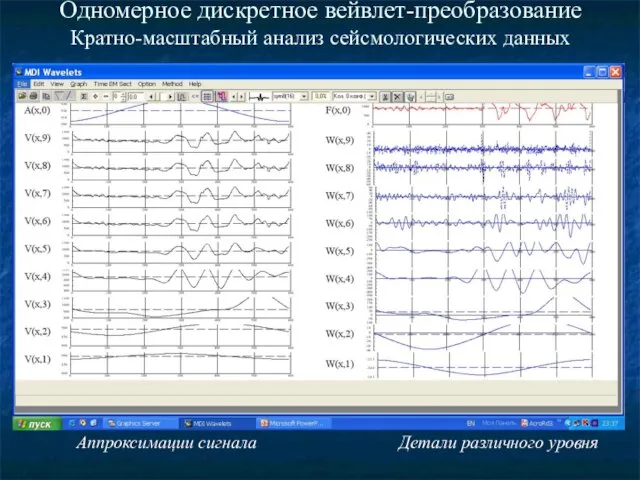
Одномерное дискретное вейвлет-преобразование Кратно-масштабный анализ сейсмологических данных
Аппроксимации сигнала
Детали различного уровня

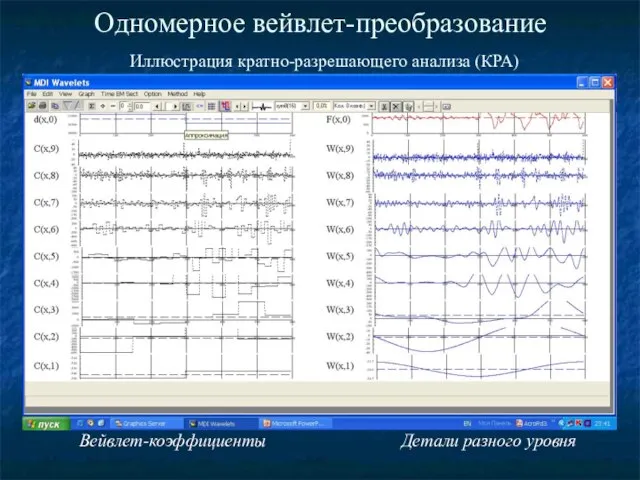
Одномерное вейвлет-преобразование
Иллюстрация кратно-разрешающего анализа (КРА)
Вейвлет-коэффициенты
Детали разного уровня

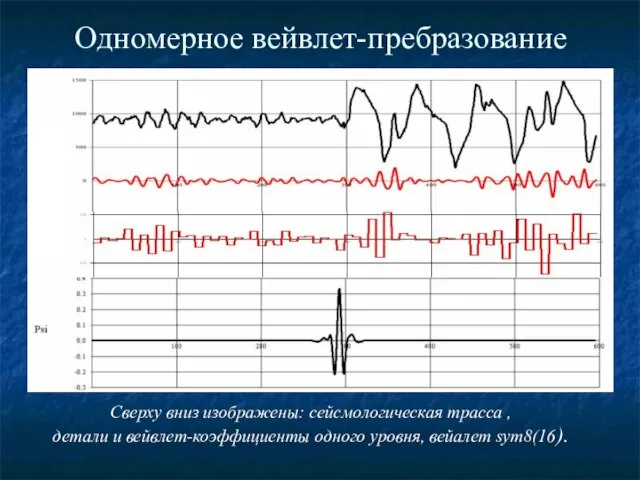
Одномерное вейвлет-пребразование
Сверху вниз изображены: сейсмологическая трасса ,
детали и вейвлет-коэффициенты одного уровня, вейалет sym8(16).

Двумерная масштабирующая функция (вверху слева)
Двумерные вейвлеты (вверху справа и внизу)

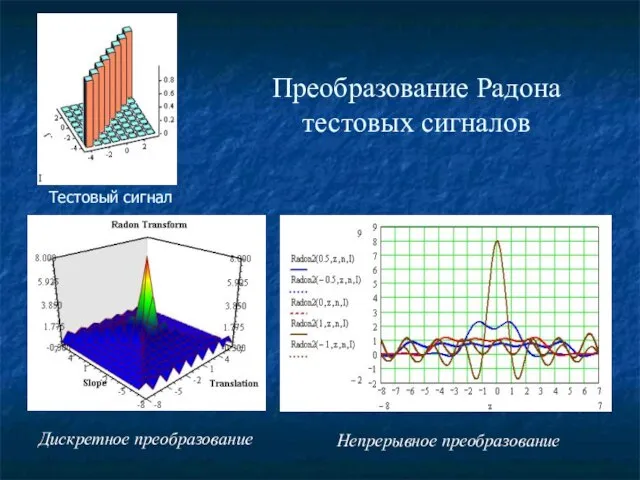
ПРЕОБРАЗОВАНИЕ РАДОНА
Двумерное преобразование Радона функции двух переменных состоит в ее интегрировании вдоль прямых.
Непрерывное преобразование Радона
Прямое преобразование Радона есть отображение функций
в функции , определяемое формулой
Обратное преобразование Радона дает формула

Преобразование Радона тестовых сигналов
Дискретное преобразование
Непрерывное преобразование
Тестовый сигнал

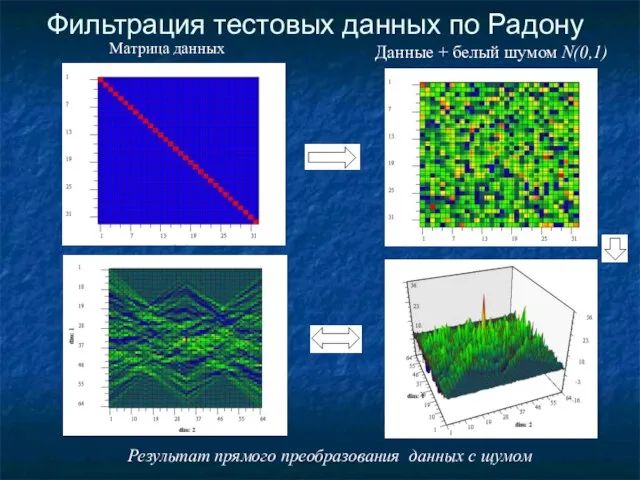
Фильтрация тестовых данных по Радону
Матрица данных
Данные + белый шумом N(0,1)
Результат прямого преобразования данных с щумом

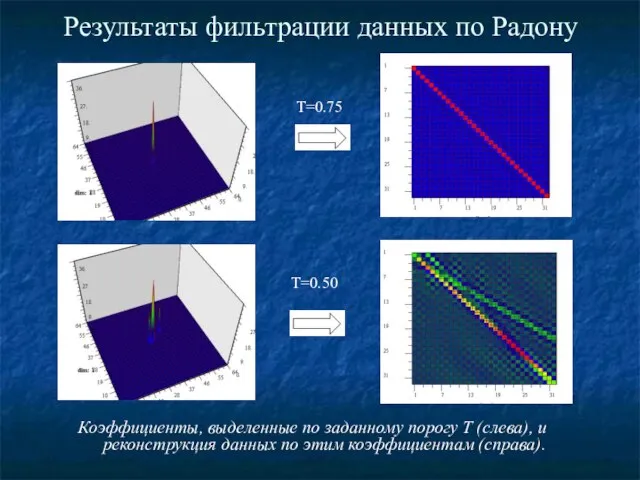
Результаты фильтрации данных по Радону
Коэффициенты, выделенные по заданному порогу Т (слева), и реконструкция данных по этим коэффициентам (справа).
Т=0.75
Т=0.50

RIDGELET TRANSFORM
(Риджлет-преобразование)
Риджлет-функции.
Пусть функция является вейвлетом.
Для любых , и определяется двумерный риджлет
Графики риджлетов.
Риджлет постоянен вдоль прямых .

Прямое непрерывное риджлет-преобразование
Пусть дана интегрируемая функция двух переменных f(x,y). Ее риджлет-преобразование определяется посредством интеграла
Обратное непрерывное риджлет-преобразование

Риджлет-анализ можно трактовать как вейвлет-анализ в области Радона. Tрансформация состоит в применении одномерного вейвлет-преобразования к строкам (или столбцам) массива Радон-коэффициентов, в направлении в которых параметр сдвига t изменяется, а угловая переменная θ является постоянной.
Одна из возможных схем риджлет-преобразования

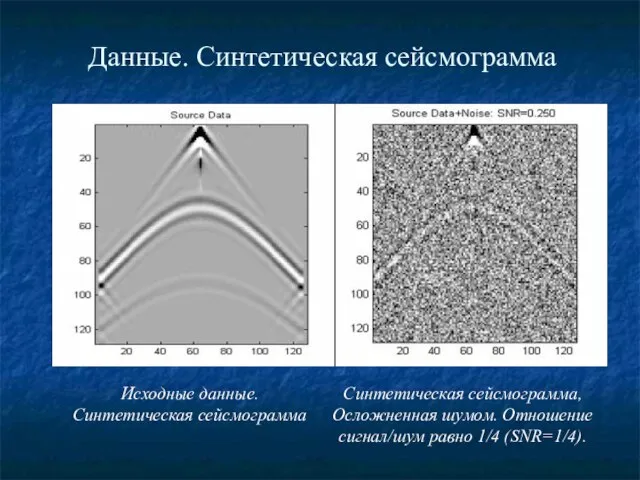
Данные. Синтетическая сейсмограмма
Исходные данные.
Синтетическая сейсмограмма
Синтетическая сейсмограмма,
Осложненная шумом. Отношение
сигнал/шум равно 1/4 (SNR=1/4).

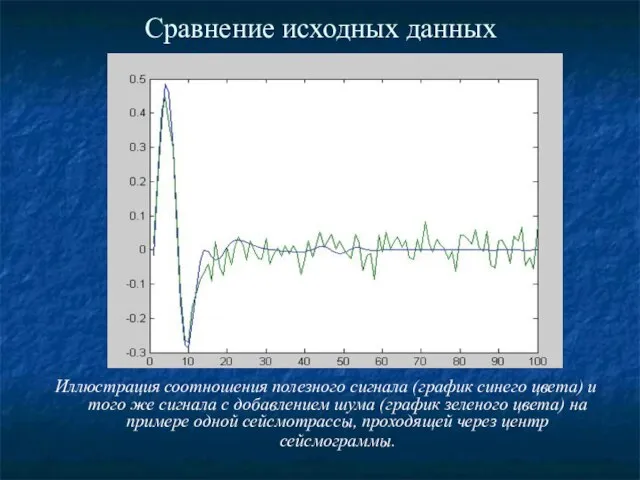
Сравнение исходных данных
Иллюстрация соотношения полезного сигнала (график синего цвета) и того же сигнала с добавлением шума (график зеленого цвета) на примере одной сейсмотрассы, проходящей через центр сейсмограммы.

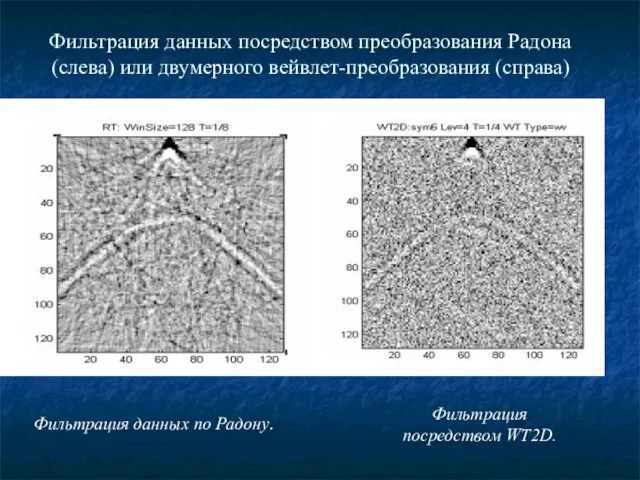
Фильтрация данных посредством преобразования Радона (слева) или двумерного вейвлет-преобразования (справа)
Фильтрация данных по Радону.
Фильтрация
посредством WT2D.

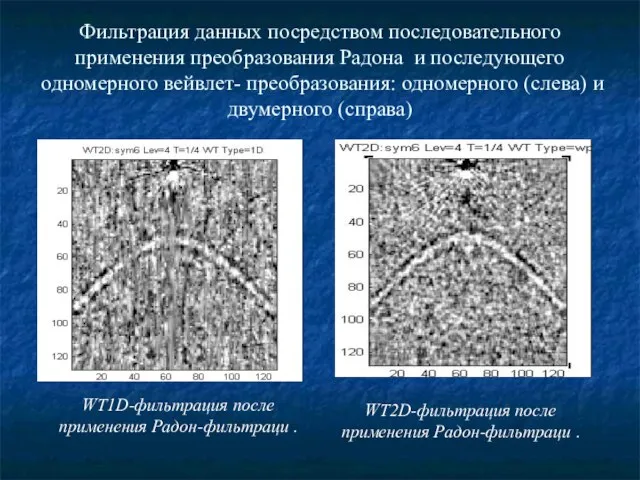
Фильтрация данных посредством последовательного применения преобразования Радона и последующего одномерного вейвлет- преобразования: одномерного (слева) и двумерного (справа)
WT1D-фильтрация после
применения Радон-фильтраци .
WT2D-фильтрация после
применения Радон-фильтраци .

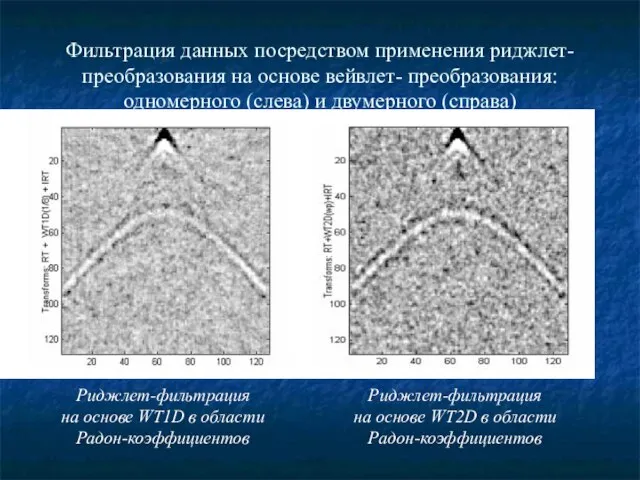
Фильтрация данных посредством применения риджлет-преобразования на основе вейвлет- преобразования: одномерного (слева) и двумерного (справа)
Риджлет-фильтрация
на основе WT1D в области
Радон-коэффициентов
Риджлет-фильтрация
на основе WT2D в области
Радон-коэффициентов

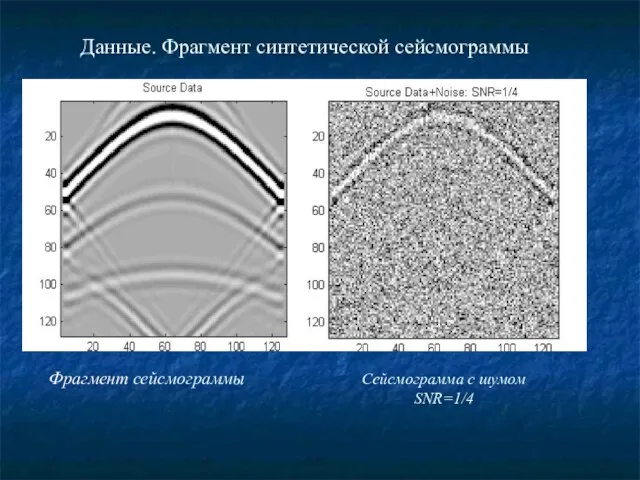
Данные. Фрагмент синтетической сейсмограммы
Фрагмент сейсмограммы
Сейсмограмма с шумом
SNR=1/4

Фильтрация данных посредством применения риджлет-преобразования на основе одномерного вейвлет- преобразования: одномерного (слева) и двумерного (справа)
Здесь использована часть сейсмограммы, не содержащая данных вблизи источника.
Риджлет-фильтрация
(RT+WT1D)
Риджлет-фильтрация
(RT+WT2D)

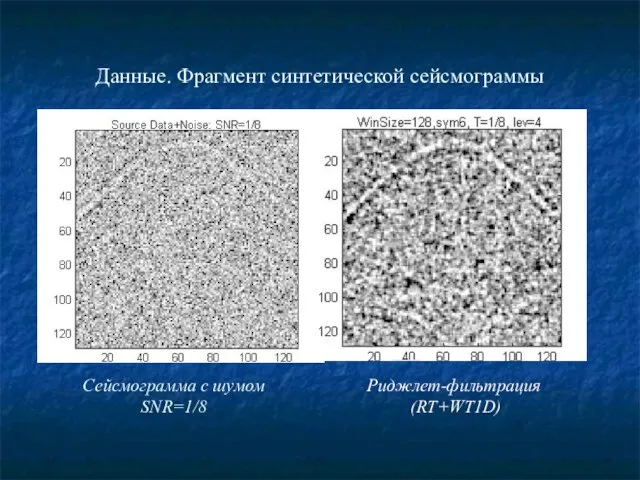
Данные. Фрагмент синтетической сейсмограммы
Сейсмограмма с шумом
SNR=1/8
Риджлет-фильтрация
(RT+WT1D)

2. Практический пример
Проиллюстрируем работу риджлет-преобразования на практических электроразведочных данных ВРЭ ЗАО «НПЦ ГЕОНЕФТЕГАЗ». Размер матрицы исходных данных 1024х64 (рис. 26).
В процессе риджлет-преобразования использовалось одномерное быстрое вейвлет-преобразование с вейвлетом ‘sym6’, порог усечения коэффициентов Tw = Т, lev = 4. Матрица данных прямоугольная, поэтому при выполнении Радон-преобразования, которое в процессе работы оперирует квадратными матрицами, использовались перекрывающиеся квадратные окна 64х64. Их наложение составляло половину ширины окна.
Результаты риджлет-фильтрации полевых данных, изображенных на рис. 26, приведены на рис. 27. Элементы, выделенные фильтрацией, весьма слабо видны на исходных данных.

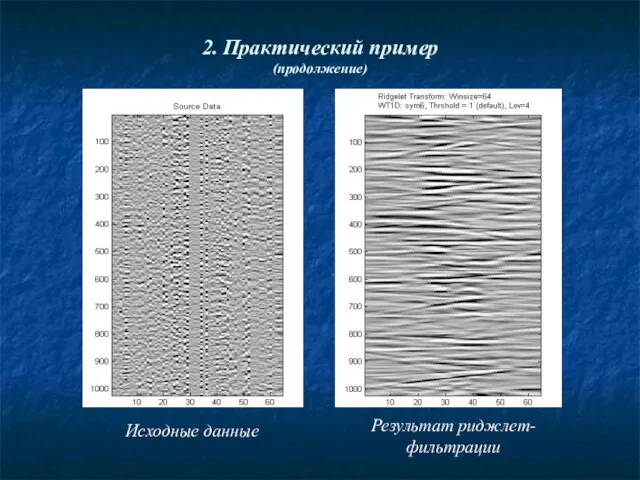
2. Практический пример
(продолжение)
Исходные данные
Результат риджлет-фильтрации

CURVELET TRANSFORM
(Курвлет-преобразование)
(Curve – кривая; изгиб, сurvelet – маленький изгиб).
Курвлет-преобразование выполняет многомасштабный анализ сигнала и состоит из выполнения двух шагов:
двумерное дискретное вейвлет-преобразование данных (WT 2D).
на каждом фиксированном масштабе, полученном в результате применения WT 2D, выполняется дискретное риджлет-преобразование.
Схема этого преобразования изображена на следующем слайде.

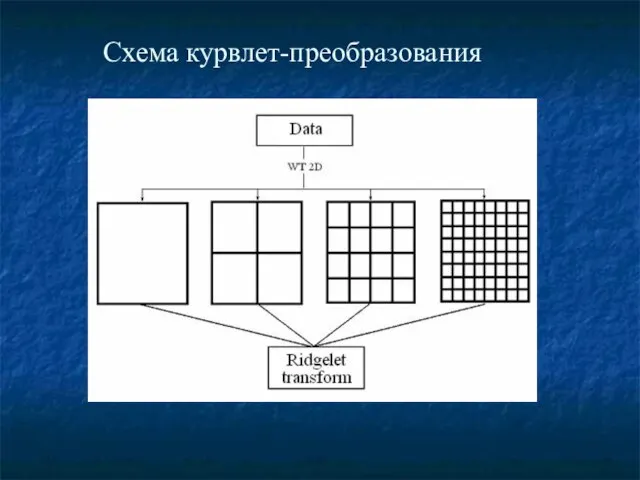
Схема курвлет-преобразования

Фильтрация изображения посредством курвлет-преобразования
Слева рисунок с шумом, справа – рисунок после курвлет-фильтрации.
Особенно хорошо восстановлены края шляпы и другие границы.
Однако вблизи граней можно увидеть осциллирующие структуры (артефакты), которых не было в исходном изображении

BEAMLET TRANSFORM
(Бимлет-преобразование)
Бимлет-преобразование реализует идею многомасштабного анализа данных (изображений), в которых линейные сегменты играют роль, аналогичную роли, которую играли точки в вейвлет-анализе.
Бимлет-структура имеет 5 ключевых компонент.
1. Бимлет-словарь – диадно-организованная библиотека линейных сегментов в семействе позиций, ориентаций и масштабов, которые дают многомасштабную аппроксимацию набора всех линейных сегментов.
2. Бимлет-преобразование образа f(x;y) - набор всех интегралов по линиям изображения вдоль бимлетов из бимлет-словаря.
3. Бимлет-пирамида является коллекцией коэффициентов бимлет-преобразования, расположенных в структуре данных с иерархической многомасштабной природой.
4. Бимлет-граф имеет структуру графа, в которой вершины соответствуют угловым пикселям в основном изображении, а грани соответствуют бимлетам, объединенным в пары таких угловых пикселей. Путь через этот граф соответствует многоугольнику в оригинальном изображении.
5. Бимлет-алгоритмы извлекают данные из бимлет-пирамиды по пути, определенном структурой бимлет-графа, например, алгоритмы движения по сети или алгоритмы рекурсивного бинарного разделения.
Используя первые четыре компонента бимлет-структуры, мы можем сформулировать базирующиеся на бимлетах алгоритмы, которые способны идентифицировать и извлекать бимлеты и цепи бимлетов со специальными свойствами

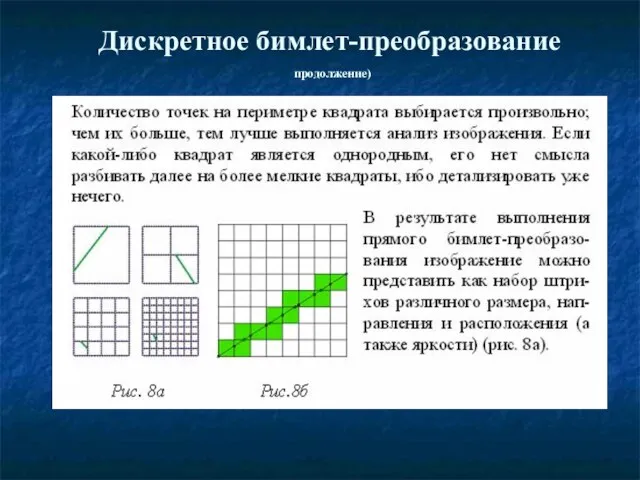
В процессе бимлет-преобразования изображение разбивается на диадическую последовательность квадратов. Для каждого такого квадрата на его сторонах отмечаются равноудаленные точки, включая вершины квадрата, и затем эти точки попарно соединяются отрезком. Полученный набор отрезков образует совокупность (коллекцию) прямых для анализа части изображения внутри этого квадрата, а их объединение для диадической последовательности всех квадратов – совокупность прямых, построенных для анализа всего изображения. В результате выполнения прямого бимлет-преобразования изображение можно представить как набор штрихов различного размера, направления и расположения (а также яркости).
Дискретное бимлет-преобразование
(продолжение)

Дискретное бимлет-преобразование
продолжение)

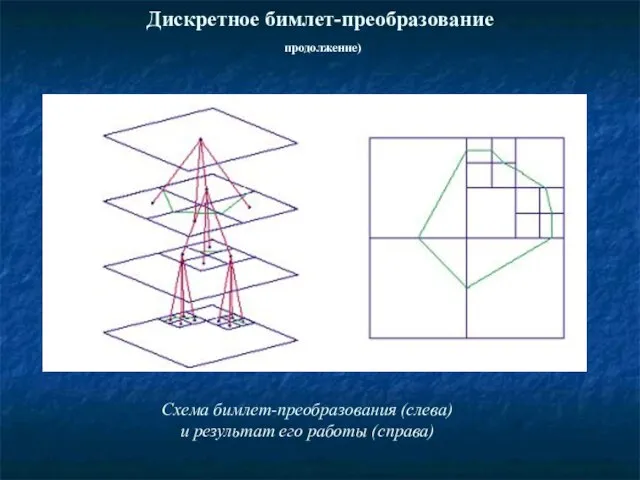
Схема бимлет-преобразования (слева)
и результат его работы (справа)
Дискретное бимлет-преобразование
продолжение)

Бимлет-преобразование.
Примеры.
Пример 1. Картина Пикассо. Выделение границ фигур на разных масштабах путем выбора коэффициентов, превышающих некоторый порог

Бимлет-преобразование. Фильтрация данных.
Пример 2. Картина Пикассо, осложненная шумом
Пример 2. Реконструкция картины посредством бимлет-фильтрации

Бимлет-преобразование.
Пример 3. Фильтрация данных посредством бимлетов
на основе двоичного разделения области на части

Литература
http://www.isye.gatech.edu/~beamlab/
http://www-stat.stanford.edu/~wavelab.
Averbuch, R. Coifman, D. Donoho, M. Israeli and J. Walden (2001). Fast Slant Stack: A notion of Radon Transform for data on a Cartesian grid which is Rapidly Computable, Algebraically Exact, Geometrically Faithful, and Invertible. Technical Report, Department of Statistics, Stanford University, Stanford, CA 94305. May.
E. J. Candès and D. L. Donoho, “Curvelets,” [Online] Available: http://www-stat.stanford.edu/~donoho/Reports/1999/curvelets.pdf, 1999.
E. Candès and D. Donoho. Ridgelets: the key to high-dimensional intermittency. Phil. Trans. R. Soc. Lond. A., 357:2495-2509, 1999.
S. Choi, D. Donoho, A. G. Flesia, X. Huo, O. Levi, D. Shi. About BeamLab – a Toolbox for New Multiscale Methodologies. Stanford University, Stanford, CA 94305 2 Georgia Institute of Technology, Atlanta, GA 30332. 7, 2002. Available: http://www-stat.stanford.edu/~beamlab.
S. R. Deans. The Radon Transform and Some of Its Applications. New York: Wiley, 1983.
D. L. Donoho. Orthonormal ridgelets and linear singularities, SIAM J. Math Anal., vol. 31, no. 5, pp. 1062–1099, 2000.
D. Donoho and X. Huo (2001). Beamlets and Multiscale Image Processing. In Multiscale and Multiresolution Methods. Eds T.J. Barth, T. Chan, and R. Haimes, Springer Lecture Notes in Computational Science and Engineering, Vol. 20, pp. 149-196.

D. Donoho and X. Huo. Beamlet pyramids: A new form of multiresolution analysis, suited for extracting lines, curves, and objects from very noisy image data. In Proceedings of SPIE, volume 4119, July 2000.
D. Donoho and O. Levi (2002). Fast X-Ray and Beamlet Transforms for Three- Dimensional Data. Technical Report, Department of Statistics, Stanford University, Stanford, CA 94305. March. In Modern Signal Processing, D. Rockmore and D. Healy, eds., Mathematical Sciences Research Institute Publications, Cambridge University Press. To appear.
D.L. Donoho Ridge Functions and Orthonormal Ridgelets. Available: http://www-stat.stanford.edu/Ridge-Ridgelet.pdf D.L.Donoho and M.R. Duncan (2000). Digital Curvelet Transform: Strategy, Implementation, Experiments. Technical Report, Department of Statistics, Stanford University, Stanford, CA 94305. March.
D.L. Donoho and A. Flesia (2001). Digital Ridgelet Transform Based on True Ridge Functions. Technical Report, Department of Statistics, Stanford University, Stanford, CA 94305. To appear in Beyond Wavelets. J. Stoeckler and G.Welland (Eds). Academic Press, December.
D.L. Donoho and M. Duncan. Digital Curvelet Transform:Strategy, Implementation and Experiments. Department of Statistics.Stanford University. November, 1999 Available: http://www-stat.stanford.edu/DCvT.pdf.
D.L. Donoho and X. Huo. Beamlet Pyramids: A New Form of Multiresolution Analysis, suited for Extracting Lines, Curves, and Objects from Very Noisy Image Data. Available: http://www-stat.stanford.edu/spie2000d2.pdf.
D.L. Donoho and X. Huo. Beamlets and Multiscale Image Analysis. Available: http://www-stat.stanford.edu/Beam070901.pdf.

Falsie, H. Hel-Or, A. Averbuch, E. Candès, R. Coifman, D. Donoho, (2002). Digital Implementation of Ridgelet Packets. Technical Report, Department of Statistics, Stanford University, Stanford, CA 94305. To appear in Beyond Wavelets. J. Stoeckler and G. Welland (Eds). Academic Press, December.
Goupilland P., Grossman A., Morlet J. Cycle-octave and related transforms in seismic signal analysis // Geoexploration,1984-1985, 23,85-102.
J.-L. Starck, D.L. Donoho, and E.J. Candès. Very High Quality Image Restoration by Combining Wavelets and Curvelets. Available: http://www-stat.stanford.edu/ spie01_vhqr.pdf.
И.Добеши. Десять лекций по вейвлетам. М., Мир, 2001.
В.П. Дьяконов. Вейвлеты. От теории к практике. СОЛОН-Пресс. М., 2004, 400 с.
Малла С. Вэйвлеты в обработке сигналов. М., Мир, 2005, 671 с.
Ф. Наттерер. Математические аспекты компьютерной томографии. М., Мир, 1990, 288 с.
Сейсмическая томография. Под ред. Г.Нолета. М., Мир,1990,416 с.
Смоленцев Н.К. Основы теории вейвлетов. Вейвлеты в МATLAB. ДМК. М., 2005, 304 с.
К.Чуи. Введение в вэйвлеты. М., Мир, 2001, 412 с.
М.Н.Юдин, Ю.А.Фарков, Д.М. Филатов. Введение в вейвлет-анализ. М., МГГА, 2000, 72 с.

Дудова К.А., Юдин М.Н. Бимлет-преобразование. Новая форма кратномасштабного анализа.//VI Международная конференция «Новые идеи в науках о земле». Материалы докладов, том IV. М., МГГРУ, 2005.
Юдин М.Н., Юдин О.М.. Исследование возможности применения бимлет-преобразо-вания, SVD-разложения и преобразования Радона для анализа данных сейсморазведки. //VI конференция Международная «Новые идеи в науках о земле». Материалы докладов, том 2, М., МГГРУ, 2005, с. 313.
Юдин М.Н., Калишенко Т. В., Юдин В.М. О применении вейвлет-преобразования и альтернирующего метода Шварца для решения некоторых задач геоэлектрики. «Новые идеи в науках о земле». Избранные доклады, М., МГГРУ, 2002, с.311-325.

Совместное применение SVD-разложения и преобразования Радона для анализа данных
Название SVD-разложение или сингулярное разложение произошло от английских слов Singular Value Decomposition.
Сингулярному разложению более ста лет. Его независимо открыли Белтрами в 1873 г. и Жордан в 1874 г. для случая квадратных матриц. В 30-е годы XX в. Эккарт и Янг распространили это разложение на прямоугольные матрицы.
Пусть А – произвольная тхп-матрица, причем m >= n. Тогда справедливо представление , где матрица U имеет размер mxn и удовлетворяет соотношению , матрица V — квадратная порядка n и удовлетворяет соотношению ,
a , где . Столбцы матрицы U называются левыми сингулярными векторами (матрицы А). Столбцы матрицы V называются правыми сингулярными векторами. Величины сигма называются сингулярными числами. (При m < n нужно рассматривать SVD транспонированной матрицы А).

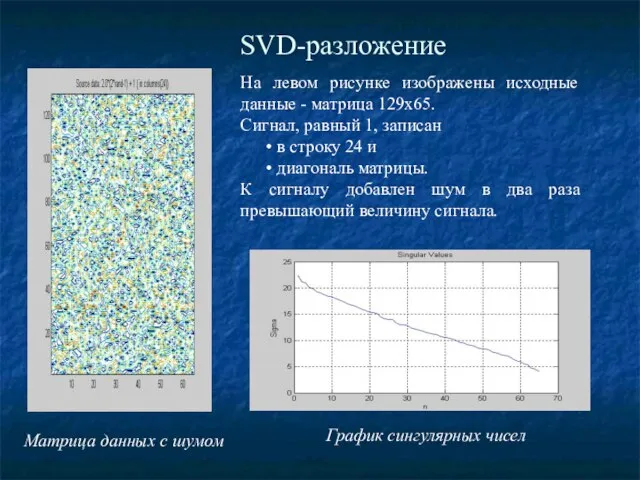
SVD-разложение
На левом рисунке изображены исходные данные - матрица 129х65.
Сигнал, равный 1, записан
в строку 24 и
диагональ матрицы.
К сигналу добавлен шум в два раза превышающий величину сигнала.
График сингулярных чисел
Матрица данных с шумом

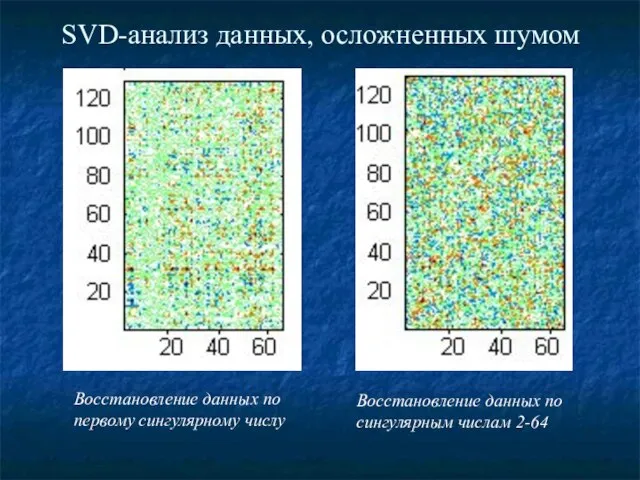
SVD-анализ данных, осложненных шумом
Восстановление данных по
первому сингулярному числу
Восстановление данных по
сингулярным числам 2-64