Содержание
- 2. Элементы выпуклого анализа. Теорема Куна-Таккера. Понятие о двойственной задаче (основные теоремы). Методы условной оптимизации. Правило множителей
- 3. Оптимизация (по латыни optimus – наилучший) - целенаправленная деятельность, заключающаяся в получении наилучших результатов при соответствующих
- 4. Решение оптимизационной задачи - это поиск определенного набора значений переменных, которому отвечает оптимальное значение критерия оптимизации.
- 5. Что можно изменять, чем можно управлять при решении задачи? Формализация задачи оптимизации 1. Определяем искомые переменные:
- 6. Формализация задачи оптимизации
- 7. Формализация задачи оптимизации
- 8. Формализация задачи оптимизации
- 9. Общая постановка задачи оптимизации Постановка задачи оптимизации содержит В векторной форме - прямые ограничения - функциональные
- 10. Примеры постановок задач оптимизации Площадь поверхности сферы равна . Какова высота цилиндра наибольшего объема, вписанногов эту
- 11. Вблизи h=3 производная меняет знак с “+” на “-”, значит при этой высоте объем цилиндра будет
- 12. Модель старинной русской задачи Пошла баба на базар, на людей посмотреть, да кое-что продать. Сколько надо
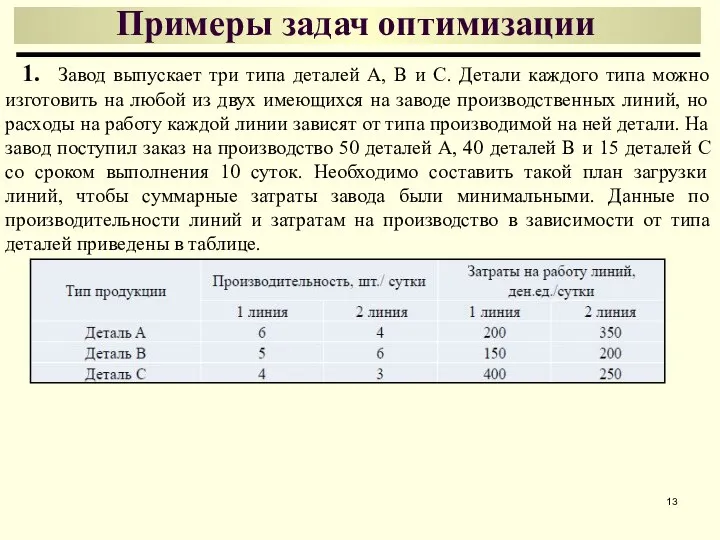
- 13. Примеры задач оптимизации 1. Завод выпускает три типа деталей А, В и С. Детали каждого типа
- 14. 2. Студент Коля любит ходить по ночным клубам и в то же время получать зачеты. Предельные
- 15. Общая постановка задачи оптимизации Постановка задачи поиска минимума функции содержит
- 16. Основные положения задачи оптимизации Замечания 2) Глобальный экстремум всегда является одновременно локальным, но не наоборот.
- 17. Основные положения задачи оптимизации
- 18. Разрешимость задачи оптимизации Теорема Вейерштрасса Следовательно, задача оптимизации разрешима, если выполняются следующие три условия: 1. Множество
- 19. Вопросы для проверки знаний Предмет и история развития методов оптимизации. Общая постановка задач оптимизации и основные
- 20. НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА 2-ОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА 1-ОЕ ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА Методы безусловной минимизации функций одной
- 21. Методы безусловной минимизации функций одной переменной Правило исследования функции на экстремум
- 22. Пример Методы безусловной минимизации функций одной переменной
- 23. Методы безусловной минимизации функций одной переменной
- 24. Прямые методы одномерного поиска Задача Минимизировать функцию одной переменной f(x) при условии , то есть найти
- 25. Определение Отрезком, соединяющим две точки и , называется множество точек x, удовлетворяющих уравнению , где .
- 26. Определение Функция f(x), заданная в выпуклой области Q, называется выпуклой или вогнутой в этой области, если
- 27. Определение Функция f(x), определенная на непустом выпуклом множестве X, называется квазивыпуклой, если для любых двух точек
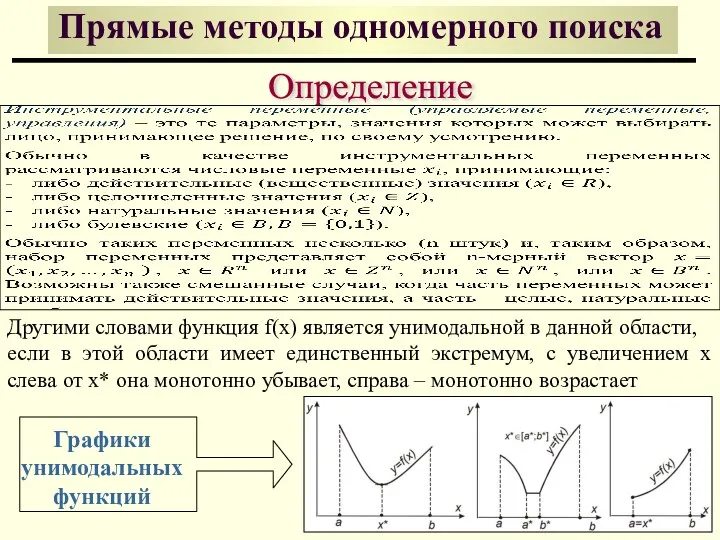
- 28. Определение Прямые методы одномерного поиска Другими словами функция f(x) является унимодальной в данной области, если в
- 29. Теорема f(x)-унимодальна или выпуклая или строго квазивыпуклая в интервале . Пусть такие, что . Если ,
- 30. Учитывая, что f(x) строго квазивыпуклая функция, имеем . Но это противоречит утверждению, что . Полученное противоречие
- 31. Стратегия поиска минимума функции одной переменной Методы исключения отрезков
- 32. Выбор начального интервала неопределенности
- 33. Выбор начального интервала неопределенности
- 34. ВЫБРАТЬ - Метод половинного деления НАЧАЛО КОНЕЦ + + -
- 35. 1 [0,5,2] 2 [2,5999,5,2] 3 [2,5999,3,90005] 4 [2,5999,3,250075] 5 [2,9248875,3,250075] 6 [2,9248875,3,08758125] 7 [2,9248875,3,006334375] 8 [2,9655109375,3,006334375]
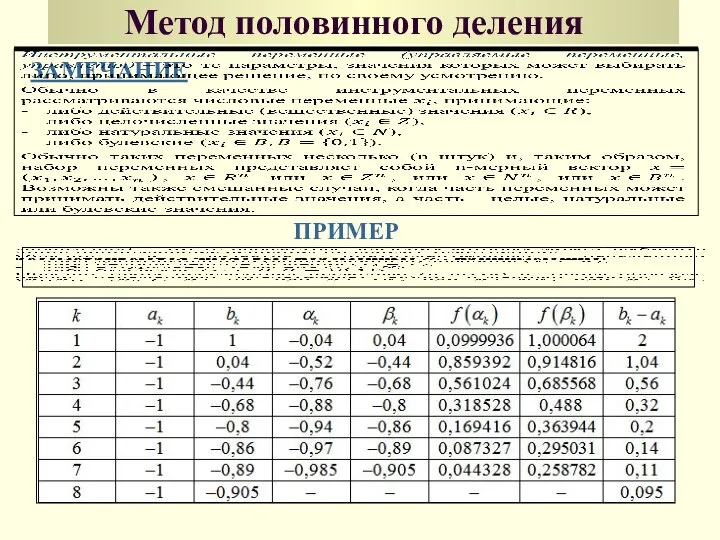
- 36. Метод половинного деления ЗАМЕЧАНИЕ ПРИМЕР
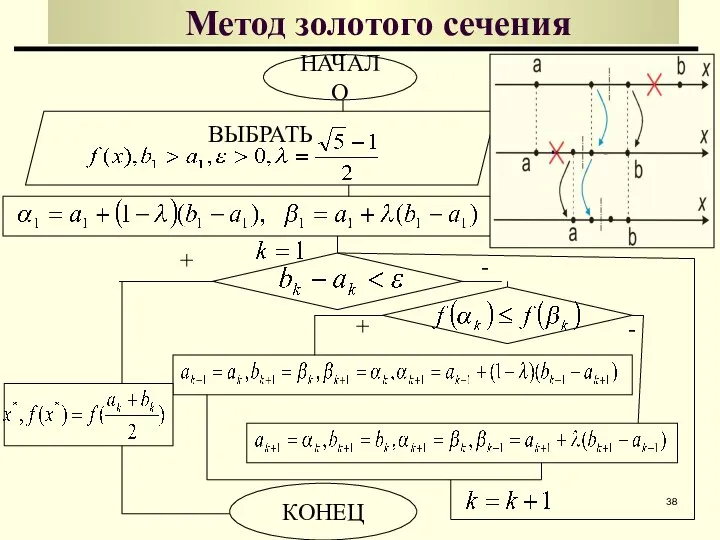
- 38. ВЫБРАТЬ - Метод золотого сечения НАЧАЛО КОНЕЦ + + -
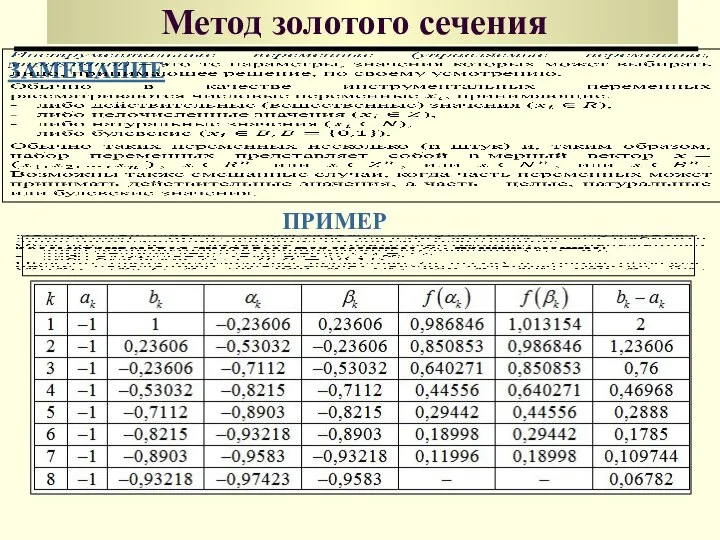
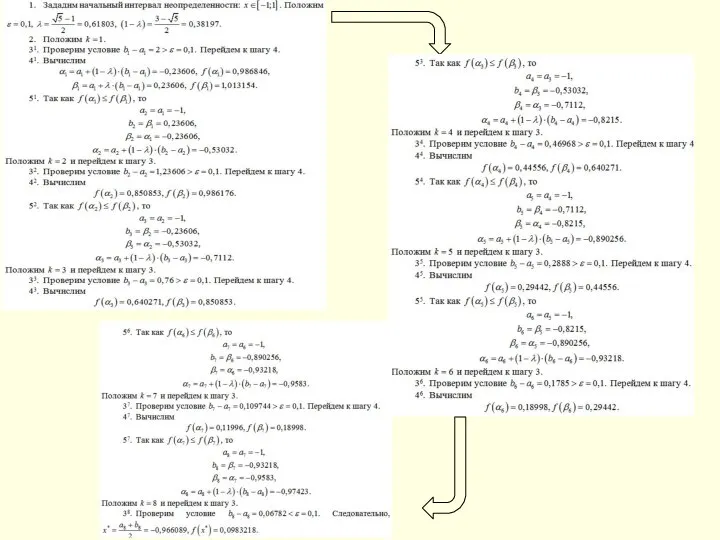
- 39. 1 [0,5,2] 2 [1,98622325850055,5,2] 3 [1,98622325850055,3,97244651700109] 4 [2,74489303400219,3,97244651700109] 5 [2,74489303400219,3,50356280950383] 6 [2,74489303400219,3,21377674149945] 7 [2,92399067349508,3,21377674149945] 8 [2,92399067349508,3,10308831298797]
- 40. Метод золотого сечения ЗАМЕЧАНИЕ ПРИМЕР
- 42. ВЫБРАТЬ - Метод Фибоначчи НАЧАЛО КОНЕЦ + + - - + -
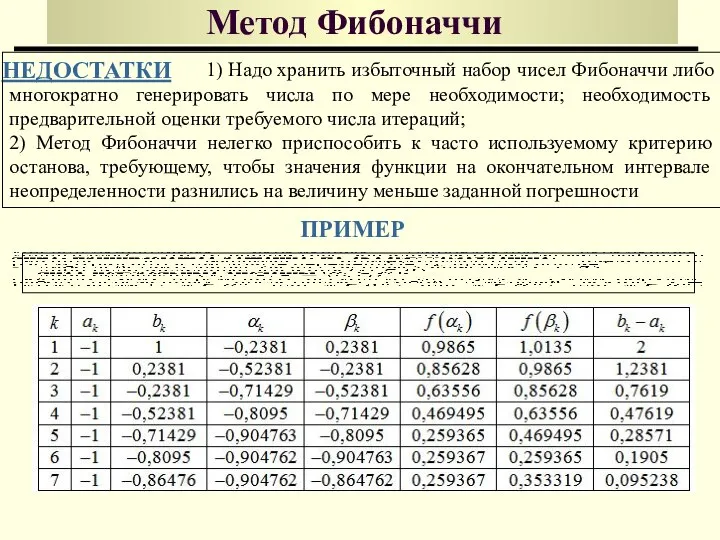
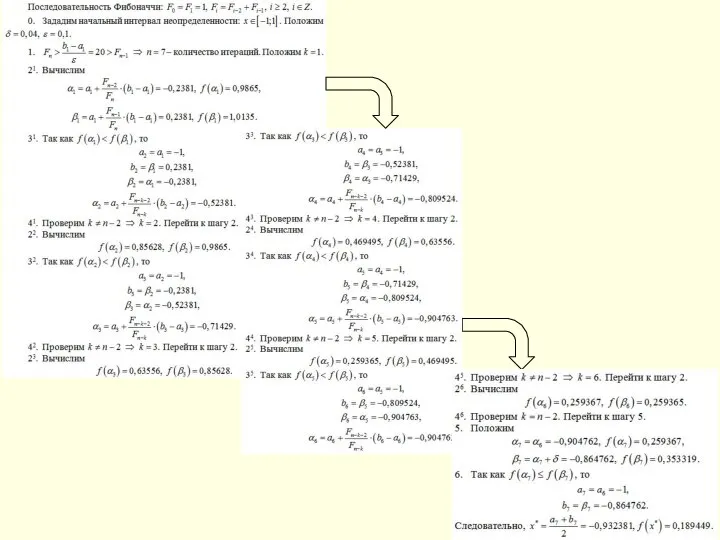
- 43. 1 [0,5,2] 2 [1,98622320768662,5,2] 3 [1,98622320768662,3,97244652899663] 4 [2,74489298777015,3,97244652899663] 5 [2,74489298777015,3,50356281125395] 6 [2,74489298777015,3,21377673233568] 7 [2,92399063683997,3,21377673233568] 8 [2,92399063683997,3,1030882961552]
- 44. Метод Фибоначчи НЕДОСТАТКИ ПРИМЕР 1) Надо хранить избыточный набор чисел Фибоначчи либо многократно генерировать числа по
- 46. - СХОДИМОСТЬ Характеристика относительного уменьшения начального интервала неопределенности находится по формуле N – количество вычислений функции
- 47. Сходимость
- 48. Метод Ньютона Выберем начальную точку Достаточное условие надежной работы метода Ньютона Замечание
- 49. Метод Ньютона Сходимость
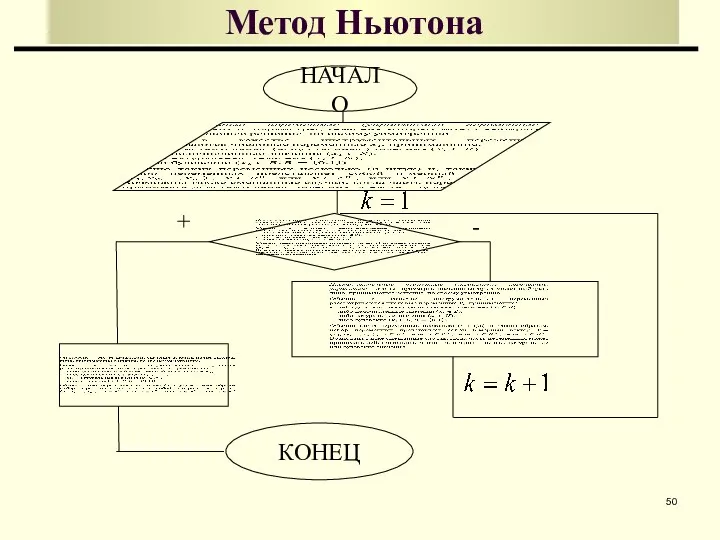
- 50. Метод Ньютона НАЧАЛО КОНЕЦ + -
- 51. ПРИМЕР
- 52. 1 [0,5,2] 2 [3,03124946640485,3,46538461538462] 3 [3,00016107700165,3,03124946640485] 4 [3,00000000432407,3,00016107700165]
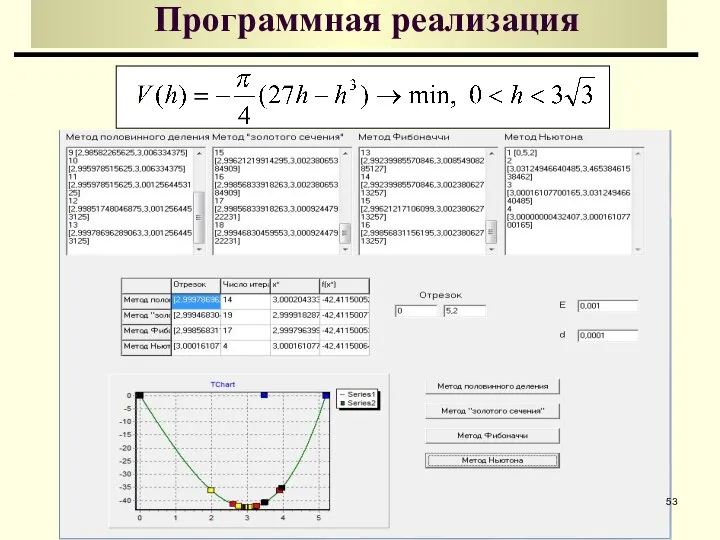
- 53. Программная реализация
- 54. Вывод Точное решение
- 55. Работа: «Методы одномерного поиска» Ознакомиться с методами одномерного поиска. Сравнить различные алгоритмы по эффективности на тестовых
- 56. Вопросы для проверки знаний - Определения отрезка, выпуклого множества, выпуклой (строго выпуклой) функции, квазивыпуклой (строго квазивыпуклой)
- 57. Примеры тестовых заданий для проверки знаний
- 59. Скачать презентацию































![1 [0,5,2] 2 [2,5999,5,2] 3 [2,5999,3,90005] 4 [2,5999,3,250075] 5 [2,9248875,3,250075] 6 [2,9248875,3,08758125]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1058812/slide-34.jpg)

![1 [0,5,2] 2 [1,98622325850055,5,2] 3 [1,98622325850055,3,97244651700109] 4 [2,74489303400219,3,97244651700109] 5 [2,74489303400219,3,50356280950383] 6 [2,74489303400219,3,21377674149945]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1058812/slide-38.jpg)

![1 [0,5,2] 2 [1,98622320768662,5,2] 3 [1,98622320768662,3,97244652899663] 4 [2,74489298777015,3,97244652899663] 5 [2,74489298777015,3,50356281125395] 6 [2,74489298777015,3,21377673233568]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1058812/slide-42.jpg)





![1 [0,5,2] 2 [3,03124946640485,3,46538461538462] 3 [3,00016107700165,3,03124946640485] 4 [3,00000000432407,3,00016107700165]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/1058812/slide-51.jpg)




 Программа развития Шаг в будущее МАУ ДО ЦДТ Юность г. Перми
Программа развития Шаг в будущее МАУ ДО ЦДТ Юность г. Перми Учреждение образования «Минское государственное профессионально-техническое училище № 114 строителей»ОТКРЫТЫЙ УРОК ПО РУССКО
Учреждение образования «Минское государственное профессионально-техническое училище № 114 строителей»ОТКРЫТЫЙ УРОК ПО РУССКО Презентация на тему Внутреннее строение Земли
Презентация на тему Внутреннее строение Земли Управление персоналом в проектах по разработке ПО
Управление персоналом в проектах по разработке ПО Презентацию выполнила Марченко Вера Владимировна E-mail:
Презентацию выполнила Марченко Вера Владимировна E-mail:  Состояние толерантности педагогов по отношению к обучающимся с ограниченными возможностями здоровья
Состояние толерантности педагогов по отношению к обучающимся с ограниченными возможностями здоровья Человек и толпа
Человек и толпа Презентация на тему Евгений Онегин (9 класс)
Презентация на тему Евгений Онегин (9 класс) Экономико-математическая модель развития ядерной энергетики России с учетом различных вариантов ядерного топливного цикла и про
Экономико-математическая модель развития ядерной энергетики России с учетом различных вариантов ядерного топливного цикла и про Click to edit Master title style Click to edit Master subtitle style
Click to edit Master title style Click to edit Master subtitle style  Международное сотрудничество в области управления природоохранной деятельностью
Международное сотрудничество в области управления природоохранной деятельностью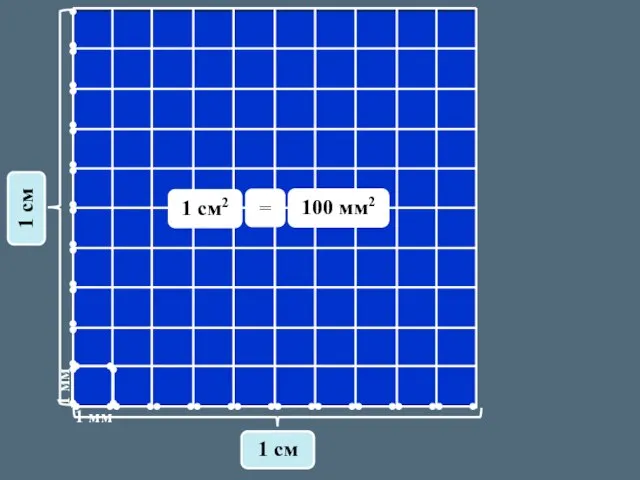 1 мм2
1 мм2 Государственная итоговая аттестация учащихся 11 классов. Инструкция для участников ЕГЭ
Государственная итоговая аттестация учащихся 11 классов. Инструкция для участников ЕГЭ Бюджетная система РФ (БС РФ): этапы становления и современные направления развития
Бюджетная система РФ (БС РФ): этапы становления и современные направления развития Презентация на тему СТЕКЛЯННЫЕ ТОВАРЫ
Презентация на тему СТЕКЛЯННЫЕ ТОВАРЫ  Организация связи и боевое применение узлов и линий связи
Организация связи и боевое применение узлов и линий связи История Чичикова
История Чичикова НОМИНАЦИЯ ОФИС
НОМИНАЦИЯ ОФИС 2013 ESC guidelines of the menedgement of stable coronary artery disease
2013 ESC guidelines of the menedgement of stable coronary artery disease Гравюры на камне из Карелии. Гравёрная мастерская Контраст
Гравюры на камне из Карелии. Гравёрная мастерская Контраст Шуляк Сергей Генеральный директор DSM Group
Шуляк Сергей Генеральный директор DSM Group Презентация на тему В.М.Васнецова «Иван-царевич на Сером Волке
Презентация на тему В.М.Васнецова «Иван-царевич на Сером Волке  Нұртас 1.10
Нұртас 1.10 Здоровье нации в твоих руках
Здоровье нации в твоих руках 9cb43e71449a428bb2724a1e53706e99 (1)
9cb43e71449a428bb2724a1e53706e99 (1) Использование лесных ресурсов при реализации приоритетных инвестиционных проектов
Использование лесных ресурсов при реализации приоритетных инвестиционных проектов Теория относительности
Теория относительности «Поисковое продвижение сайтов»
«Поисковое продвижение сайтов»