Модель фильтрации Бакли-Леверетта и применение этой модели

Практическая важность изучения двухфазных течений в пористых средах
При проектировании и анализе разработки нефтяных и газовых месторождений при-ходится исследовать совместное течение в пористой среде нескольких жидкостей.
При разработке нефтяных и газо-вых месторождений практически всегда возникает двух- или трехфазное течение, поскольку силы, движущие нефть, являют-ся следствием упругости или гидродина-мического напора газа и воды.

Теория двухфазной фильтрации несмешивающихся жидкостей
В случае одномерного течения несжимаемых не-смешивающихся жидкостей в условиях, когда поверхностное натяжение между фазами невели-ко и можно пренебречь капиллярным давлением, а также влиянием силы тяжести, процесс вытес-нения допускает простое математическое описа-ние, предложенное С. Бакли и М. Левереттом. Их описание основано на понятиях насыщенности и относительных фазовых проницаемостей и использовании обобщенного закона Дарси.

Относительная фазовая проницаемость – отно-шение проницаемости породы для одной из фаз, движущейся в порах многофазной системы, к абсолютной проницаемости.
Насыщенность порового пространства некото - рой i-й фазой (si) – доля объема пор в элемен-тарном макрообъеме, охватывающем данную произвольную точку, занятого i-й фазой.
Скорость фильтрации – объемный расход жидкости, приходящийся на единицу поперечного сечения пласта, - фиктивная скорость, с которой двигалась бы жидкость, если бы пористая среда отсутствовала и движение происходило в свободном пространстве, ограниченном кровлей и подошвой пласта.

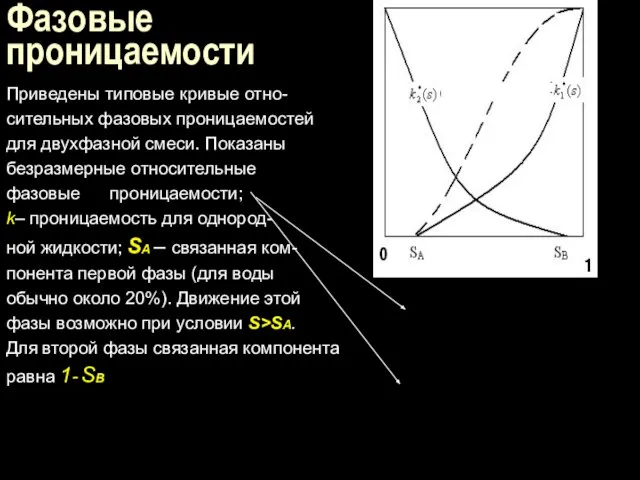
Фазовые проницаемости
Приведены типовые кривые отно-
сительных фазовых проницаемостей
для двухфазной смеси. Показаны
безразмерные относительные
фазовые проницаемости;
k– проницаемость для однород-
ной жидкости; SA – связанная ком-
понента первой фазы (для воды
обычно около 20%). Движение этой
фазы возможно при условии S>SA.
Для второй фазы связанная компонента
равна 1- SB

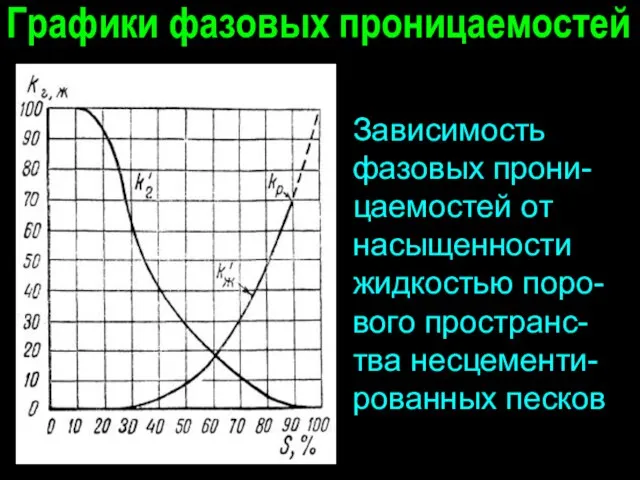
Графики фазовых проницаемостей
Зависимость фазовых прони-цаемостей от насыщенности жидкостью поро-вого пространс-тва несцементи-рованных песков

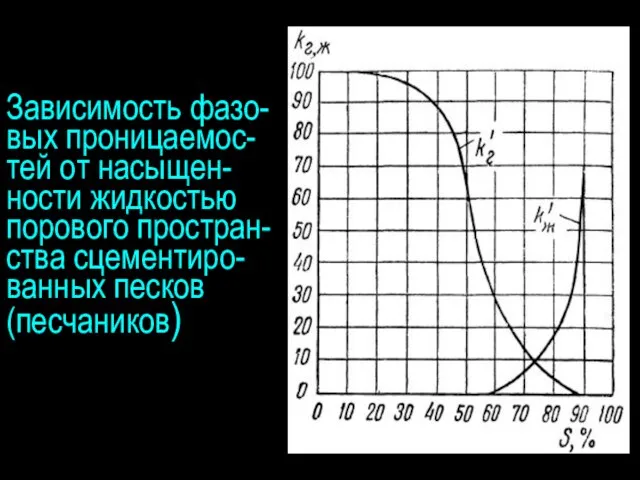
Зависимость фазо-вых проницаемос-тей от насыщен-ности жидкостью порового простран-ства сцементиро-ванных песков
(песчаников)

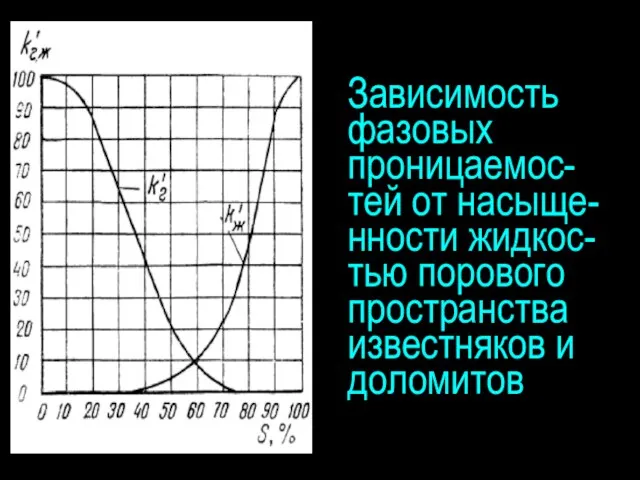
Зависимость фазовых проницаемос-тей от насыще-нности жидкос-тью порового пространства известняков и доломитов

Анализ графиков фазовых проницаемостей
При наличии в поровом пространстве несцементи-рованных песков и известняков до 20% жидкости (S = 20% ), а в порах песчаников (сцементирован-ных песков) до 50% жидкости, фазовая проницае-мость для жидкой фазы газированной жидкости k'Ж=0, а относительная проницаемость для газооб-разной фазы смеси k'Г = 90% для несцементиро-ванных песков и известняков и k'Г = 98% для пес-чаников (при S = 20% , а при S = 50% имеем k'Г = 65% для песков-песчаников) Таким образом, жид-кость, скопляясь в порах, мало мешает прохожде-нию газа.

При содержании в порах песка и песчаника до 20% газа, а в порах известняка до 30% газа фазовая проницаемость для газа мала, т.е. газ почти целиком остается в порах, но в отличие от жидкости он сильно мешает фильтрации жидкости, снижая относительную проницае-мость k'ж до ~ 20% для известняков, до 48% для несцементированных песков и до ~ 18 % для песчаников. Это указывает на отрицательные черты эксплуатации нефтяных месторождений при режиме растворенного газа, поскольку ха-рактерное для этого режима наличие в поровом пространстве пласта пузырьков окклюдирован-ного газа приводит к указанному чрезвычайно резкому уменьшению фазовой проницаемости пласта для нефти.

Анализ одномерных течений позволяет:
- выявить основные эффекты совместной фильтрации двух жидкостей; - выявить характерные особенности совместной фильтрации двух жидкостей;
- сопоставить полученные данные с результатами лабораторных экспериментов.

Модель основана на следующих допущениях :
1.Процесс вытеснения рассматривается в прямолинейном тонком горизонтальном образце;
2.Образец состоит из однородной и изотропной пористой среды (пористость и проницаемость постоянны);
3.Поперечное сечение образца на столько мало, что давление и насыщенность можно считать постоянными по сечению;
4.Давление р в нефтяной и водяной фазах одинаковы в силу пренебрежения капиллярным давлением;
5.Обе фазы несжимаемы, их температура постоянна;

ФИЗИЧЕСКИЕ ПРЕДСТАВЛЕНИЯ И МАТЕМАТИЧЕСКОЕ ОПИСАНИЕ ПРОЦЕССА ВЫТЕСНЕНИЯ ОДНОЙ ЖИДКОСТИ ДРУГОЙ
проведение эксперимента:
1.В рассматриваемый образец через сечение x=0 закачивается вода. 2.В процессе вытеснения образуется зона совместного движения воды и нефти.
3.Образуется связная система.
4.Из-за избирательной смачиваемости твердой породы водой площадь контакта каждой из фаз со скелетом пористой среды значительно пре-вышает площадь контакта фаз между собой. Это позволяет считать, что основной вклад в сопротивление движению дает взаимодействие каждого флюида с твердым скелетом пласта, и пренебречь эффектом увлечения одной жидкостью другой.

По дифференциальному закону Дарси закон фильтрации для каждой из фаз:
Для воды : Для нефти:
где wВ , Qв и wН, Qн – скорости фильтрации и объемные расходы соответственно воды и нефти; ηв , ηн - коэффициенты динамической вязкости фаз; kв(s) и kн(s)- относительные фазовые проницаемости; s = sв – водонасыщенность

Для вывода уравнения неразрывности рассмотрим баланс водной фазы в макрообъеме :
Через сечение с координатой X за промежуток времени Δt втекает в объем ΔV масса воды
А вытекает через сечение x+ΔX масса, равная
изменение массы воды в объеме ΔV за время Δt равно :
где

продолжение
С другой стороны, это изменение массы должно быть сбалансировано за счет изменения во времени водонасыщенности в поровом объеме mΔV :
приравняв выражения для изменения массы и разделив обе части на ρвΔVΔt , получим: (1)
Аналогично для нефти:
или (2)

продолжение
Сложив уравнения неразрывнос –
ти для обеих фаз (1 и 2), получаем:
Эти равенства показывают, что суммарная скорость w
и суммарный расход фаз Q не зависят от координаты и является либо постоянной величиной, либо известной функцией времени.

Функция Бакли-Леверетта
1.Поделим почленно одно на другое уравнения
и
2. Получим где
3.Применив к последнему равенству выражение суммарных скорости фильтрации и дебита, получим:
Введем функцию f :

Функция
называется функцией распределения потоков фаз или функцией Бакли-Леверетта

Физический смысл функции Бакли-Леверетта:
f(s), представляющая отношение скорости фильтрации (или рас-хода) вытесняющей фазы (воды) и суммарной скорости w(t)
(или расхода Q(t)), равна объемной доле воды в суммарном потоке двух фаз.

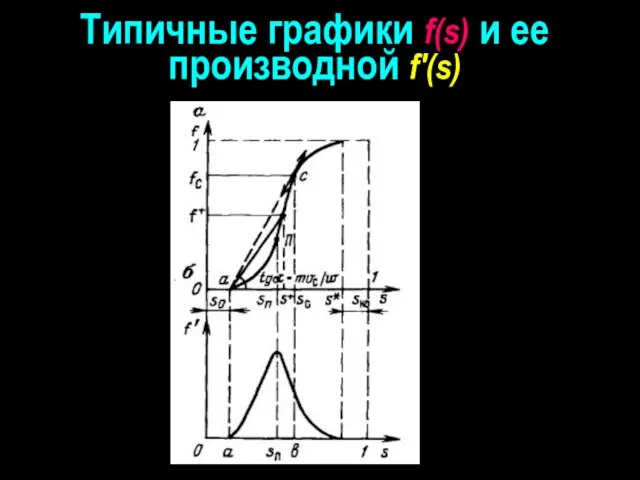
Типичные графики f(s) и ее производной f'(s)

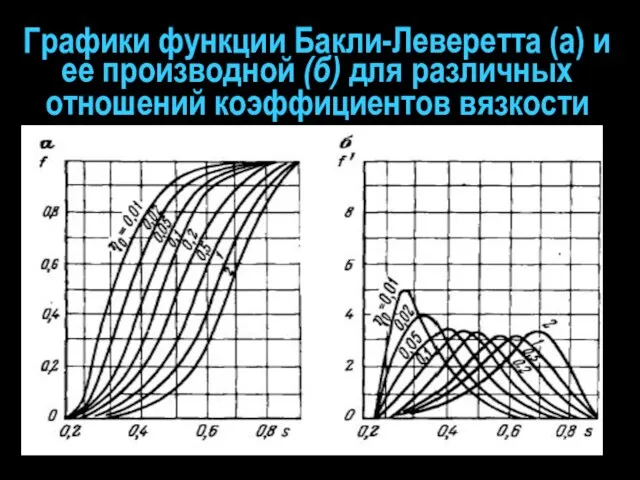
Графики функции Бакли-Леверетта (а) и ее производной (б) для различных отношений коэффициентов вязкости

Производная функции Бакли-Леверетта f'(s) определяет скорость распространения насыщенности зада-нной величины. Одному и тому же зна-чению f'(s) соответствует два разных значения насыщенности s. Это означа-ет, что, начиная с некоторого момента, распределение насыщенности стано-вится многозначным, чего физически невозможно. Многозначность означает, что в зоне движения двухфазной жид-кости имеет место скачок насыщеннос-ти. Насыщенность на скачке называет-ся фронтовой насыщенностью.

Модель фильтрации Бакли-Леверетта позволяет решать следующие задачи:
1.Определение фронтальной насыщенности;
2.Определение средней насыщенности в безводный период добычи;
3. Расчет средней насыщенности после прорыва воды;
4. Расчет коэффициента нефтеотдачи.

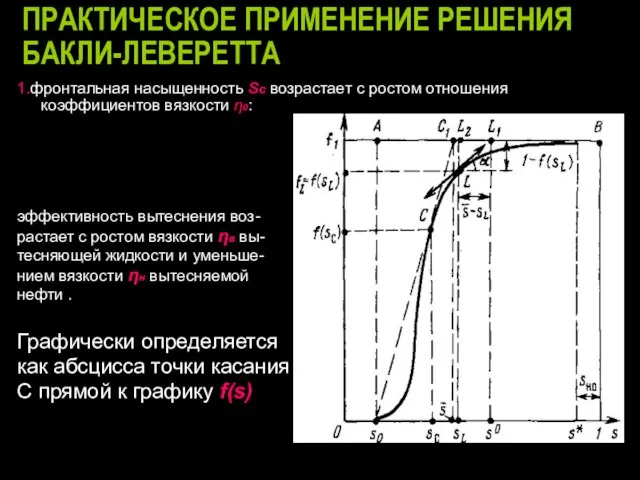
ПРАКТИЧЕСКОЕ ПРИМЕНЕНИЕ РЕШЕНИЯ БАКЛИ-ЛЕВЕРЕТТА
1.фронтальная насыщенность sс возрастает с ростом отношения коэффициентов вязкости η0:
эффективность вытеснения воз-
растает с ростом вязкости ηв вы-
тесняющей жидкости и уменьше-
нием вязкости ηн вытесняемой
нефти .
Графически определяется
как абсцисса точки касания
С прямой к графику f(s)

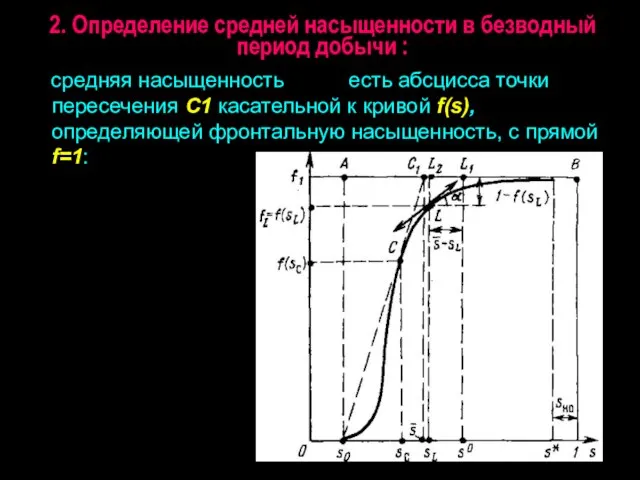
2. Определение средней насыщенности в безводный период добычи :
средняя насыщенность есть абсцисса точки пересечения С1 касательной к кривой f(s), определяющей фронтальную насыщенность, с прямой f=1:

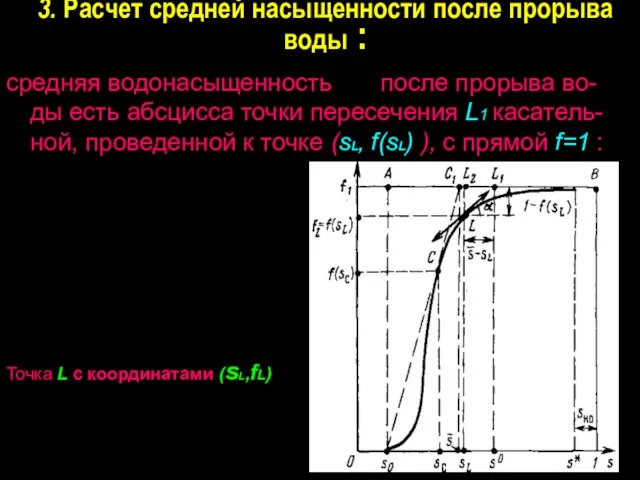
3. Расчет средней насыщенности после прорыва воды :
средняя водонасыщенность после прорыва во-ды есть абсцисса точки пересечения L1 касатель-ной, проведенной к точке (sL, f(sL) ), с прямой f=1 :
Точка L с координатами (sL,fL)

4. Расчет коэффициента безводной нефтеотдачи.
Для модельных относительных фазовых проницаемостей
и соответствующей функции распределения фаз
получено выражение для коэффициента нефтеотдачи :
где
Коэффициент безводной нефтеотдачи увеличивается при увеличении вязкости вытесняющей фазы или уменьшении вязкости вытесняемой фазы.