Содержание
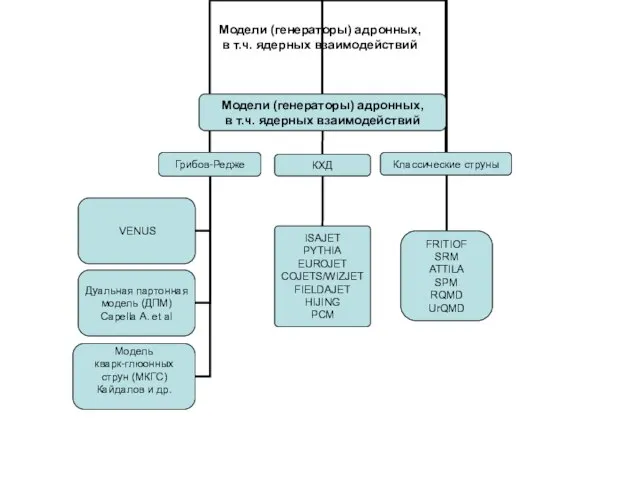
- 2. Модели (генераторы) адронных, в т.ч. ядерных взаимодействий
- 3. Связь КХД с теорией Редже Рост сильной константы связи αs(Q2) в мягких процессах Альтернативный малый параметр
- 4. Модель кварк-глюонных струн 1/N разложение в КХД – полуфеноменологическая теория + модель цветной трубки и кварк-глюонных
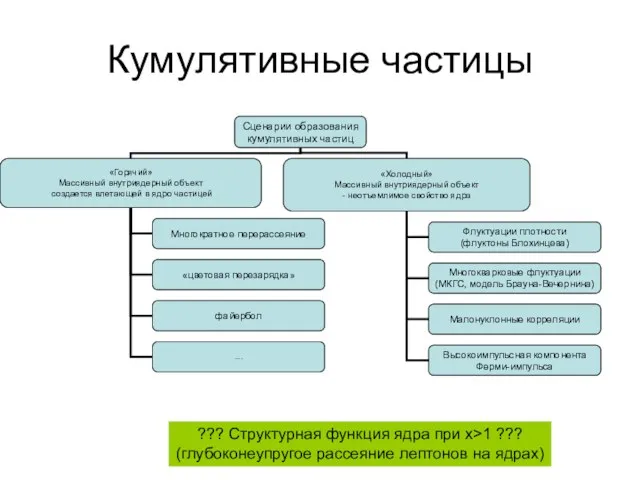
- 5. Кумулятивные частицы ??? Структурная функция ядра при x>1 ??? (глубоконеупругое рассеяние лептонов на ядрах)
- 6. Общие свойства большинства «холодных» моделей Инвариантное сечение процесса AB -> hX для частицы h в области
- 7. Различные виды функций fhB Предельная фрагментация и модель слияния дают: т.е. сечение ~ FA(x) Модель жёсткого
- 8. Тогда (в т.ч. и в кумулятивной области x>1): При этом многокварковые флуктуации (точнее малонуклонные корреляции) дают
- 9. Анализ EMC + независимость уравнений эволюции КХД от сорта мишени показывает, что: 1) существует 2 независимых
- 10. А для частиц с валентными кварками ядра можно положить TA≈TANS≈TAS и использовать с нормировками Т.е. можно
- 11. Все предыдущие выводы – безмодельны, в рамках «холодного» сценария Теперь попробуем вычислить TA(α) в МКГС. Наличие
- 12. МКГС(1) Использовались T1(α) - для Парижской ВФ и – в соответствие с МКГС (пересечение бозонной и
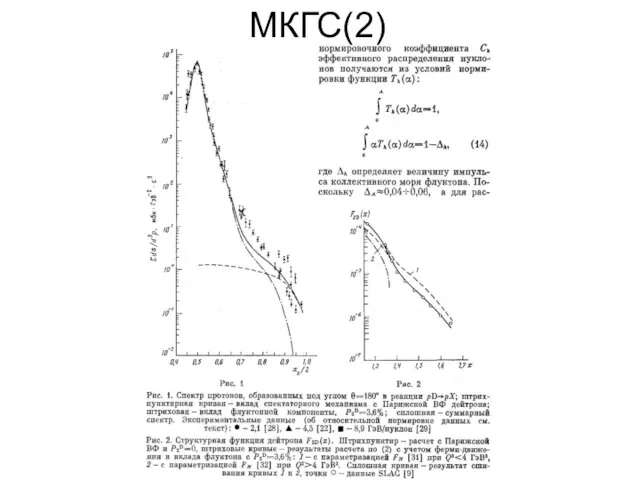
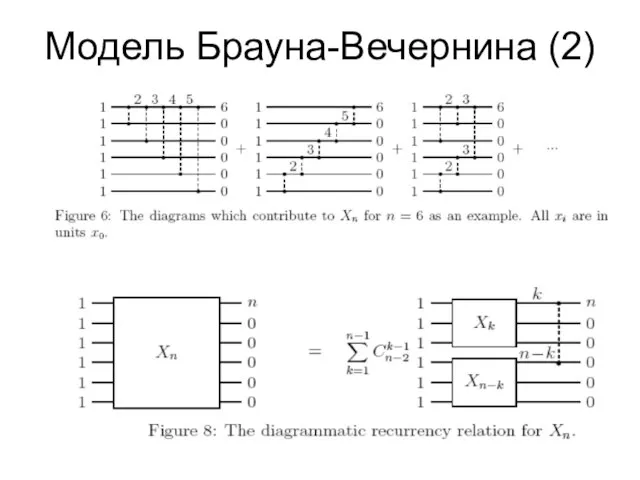
- 13. МКГС(2)
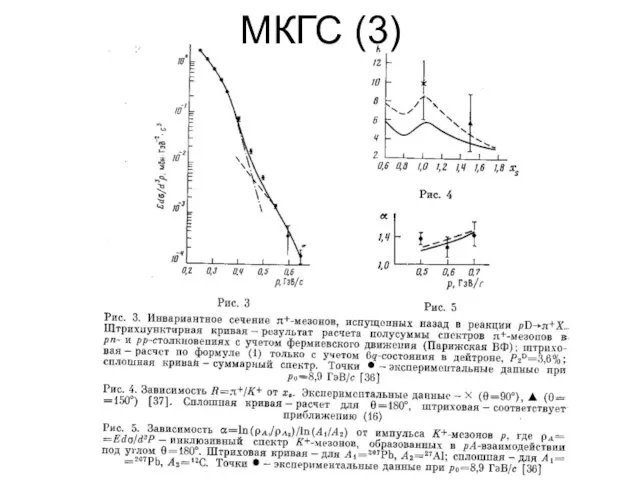
- 14. МКГС (3)
- 15. Описание данных при больших pt Двухкомпонентная дуальная топологическая модель (вариант топологического 1/N разложения) «Мягкий» (надкритический) померон
- 16. Модель Брауна-Вечернина (суммирование кварк-партонных диаграмм на порогах) В МКГС – феноменологическое описание кумулятива, основанное ядерных кварковых
- 17. Модель Брауна-Вечернина (1)
- 18. Модель Брауна-Вечернина (2)
- 19. Модель Брауна-Вечернина (3) where the slope b0 is determined by the QCD coupling constant and quark
- 21. Скачать презентацию













 Полевые сорняки
Полевые сорняки Наглядная агитация отряда № 2
Наглядная агитация отряда № 2 Угроза за спиной
Угроза за спиной DIPLOMATIC SERVICE
DIPLOMATIC SERVICE Жизнь как деяние
Жизнь как деяние Сохранить природу-сохранить жизнь.
Сохранить природу-сохранить жизнь. Модернізація причального контейнерного перевантажувача вантажопідйомністю 50 т
Модернізація причального контейнерного перевантажувача вантажопідйомністю 50 т Группа компаний МАСКОМ Компания Digital Security ТЕМА: Выполнение требований 152 ФЗ и PCI DSS в современных информационных системах - эффект с
Группа компаний МАСКОМ Компания Digital Security ТЕМА: Выполнение требований 152 ФЗ и PCI DSS в современных информационных системах - эффект с Кухня. Стеллажи
Кухня. Стеллажи Организация обучения по подготовке аудиторов в учебных центрах
Организация обучения по подготовке аудиторов в учебных центрах ОРУЖИЕ ПОБЕДЫ
ОРУЖИЕ ПОБЕДЫ таблица на 2
таблица на 2 Презентация на тему методическая система
Презентация на тему методическая система  Кто хочет стать миллионером? 8 класс
Кто хочет стать миллионером? 8 класс ИНФОРМАЦИЯ О КОМПАНИИ
ИНФОРМАЦИЯ О КОМПАНИИ Вода – особенная жидкость
Вода – особенная жидкость Эти загадочные пирамиды
Эти загадочные пирамиды Исследование силовой подготовки девушек и женщин, занимающихся фитнесом
Исследование силовой подготовки девушек и женщин, занимающихся фитнесом Яблочно-молочное брожение (ЯМБ)
Яблочно-молочное брожение (ЯМБ) «Платок в квадрате» Музей истории русского платка и шали (Московская область) Номинация «Партнерские музейные проекты» Руковод
«Платок в квадрате» Музей истории русского платка и шали (Московская область) Номинация «Партнерские музейные проекты» Руковод Фотовыставка Несовместимы дети и война
Фотовыставка Несовместимы дети и война Ценные свойства козьего молока и продуктов из него. 3 класс
Ценные свойства козьего молока и продуктов из него. 3 класс Магазин 5 Элемент
Магазин 5 Элемент Технология и оборудование для изготовления горячей штамповкой номенклатуры деталей типа вилка
Технология и оборудование для изготовления горячей штамповкой номенклатуры деталей типа вилка Инструкция по замене разработки пользователя на сайте «Учительский портал» http://www.uchportal.ru/
Инструкция по замене разработки пользователя на сайте «Учительский портал» http://www.uchportal.ru/ Н и НН в суффиксах имен прилагательных
Н и НН в суффиксах имен прилагательных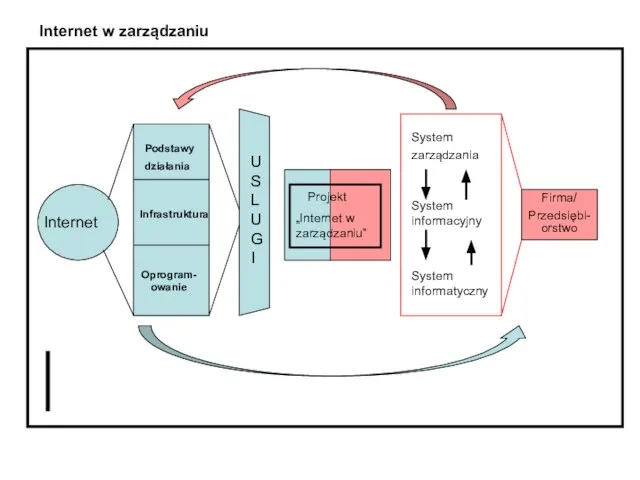 Internet w zarzadzaniu
Internet w zarzadzaniu Музы Сергея Есенина
Музы Сергея Есенина