Модели повышения эффективности передачи данных при использовании протокола ТСР

Особенности AIMD
Средняя скорость ограничена
В среднем используется ¾ доступной полосы пропускания
Наличие сильных осцилляций скорости передачи данных

Ограниченность скорости
Возрастание скорости передачи данных от
до происходит по правилу арифметической
прогрессии

Колебания скорости передачи данных
Неполное использование ресурсов
Глобальные осцилляции
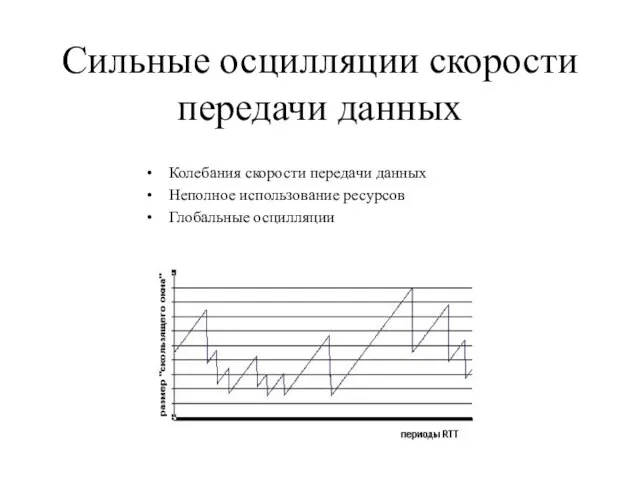
Сильные осцилляции скорости передачи данных

Математическая модель алгоритма
Индекс справедливости

Математические свойства модели
Верно соотношение:
Если aI >0, тогда F монотонно возрастает
Если aI >0, тогда
Если , то система стремится к справедливым состояниям

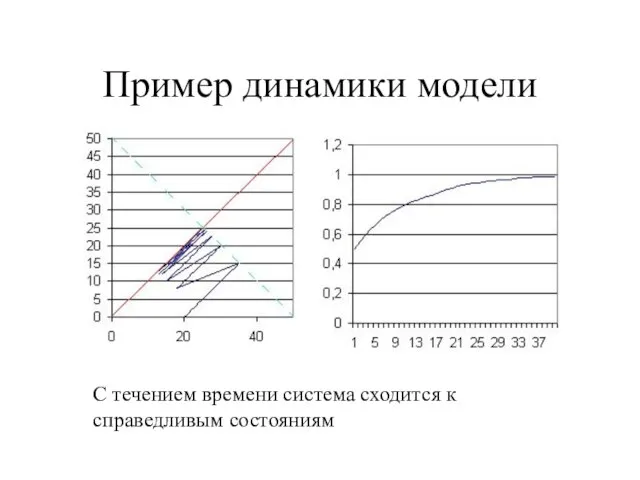
Пример динамики модели
С течением времени система сходится к
справедливым состояниям

MAIMD и AIMD
Для MAIMD неверно утверждение о сходимости к справедливым состояниям
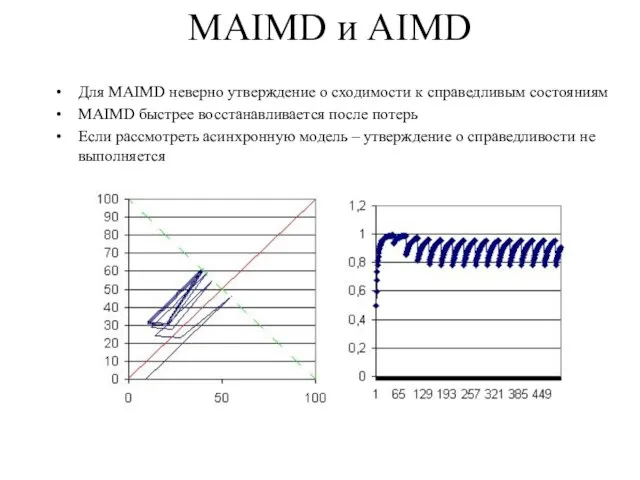
MAIMD быстрее восстанавливается после потерь
Если рассмотреть асинхронную модель – утверждение о справедливости не выполняется

Простейший метод повышения производительности – масштабирование
Увеличение размера MTU в n раз
Использование n параллельных потоков ТСР
Использование алгоритма AIMD с aI=n

Методы с переменными параметрами
Метод виртуального MTU
Метод заданной средней скоростью

Метод виртуального MTU
Вводим виртуальный MTU v=[bm/l]
Получаем в результате
Особенность метода: экспоненциальный
рост скорости передачи данных

Метод с заданием средней скорости
Рассмотрим две пары (P,W) и (P1,W1) - какие мы хотим получить размеры окна при различных частотах потери
Из этого соотношения можно подобрать нужные параметры AIMD алгоритма:

Метод, основанный на характеристическом уравнении
Требуется, чтобы алгоритм модификации окна удовлетворял
Оценка среднего интервала между событиями потери:
По построенной оценке выбирается размер «окна» так, чтобы выполнялось характеристическое соотношение

Эвристика групп Пуассона
События потери располагаются во времени неравномерно
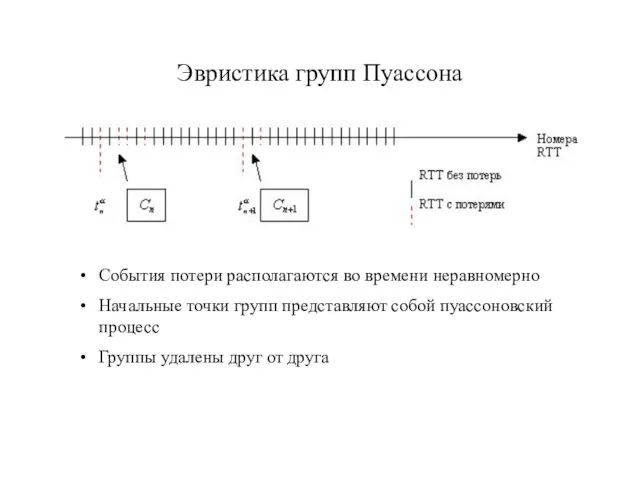
Начальные точки групп представляют собой пуассоновский процесс
Группы удалены друг от друга

В результате возникают задачи
Выделить из событий потери группы
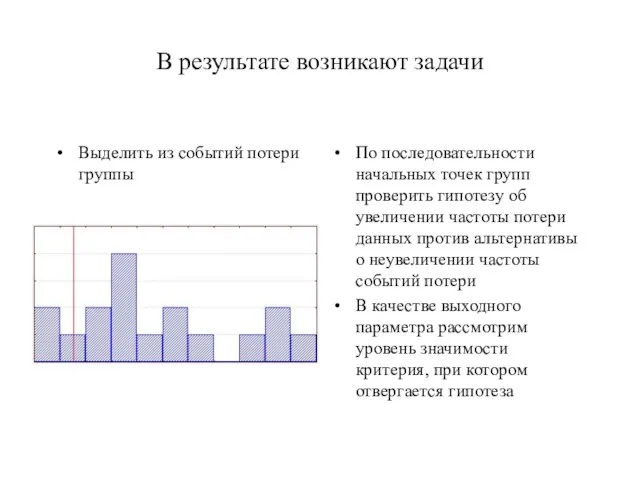
По последовательности начальных точек групп проверить гипотезу об увеличении частоты потери данных против альтернативы о неувеличении частоты событий потери
В качестве выходного параметра рассмотрим уровень значимости критерия, при котором отвергается гипотеза

Модель с параметрами – случайными величинами
р – уровень правдоподобие гипотезы о ухудшении
состояния сети