Модели со стохастическими регрессорами

Модели со стохастическими регрессорами
Ранее мы предполагали, что COV(xi,ui)=0
На практике это не всегда справедливо.
Причины:
1. В моделях временных рядов, регрессоры являются функциями времени, что приводит к их корреляции со случайными возмущениями
2. Регрессоры измеряются с ошибками т.е являются случайными величинами
3. Использование лаговых переменных

Модели со стохастическими регрессорами
Возможны три ситуации:
1. В уравнениях модели отсутствует корреляция между регрессорами и случайным возмущением (COV(xi,ui)=0 (оценки несмещенные и эффективные)
2. Регрессоры не коррелируют со случайными возмущениями в текущих наблюдениях, но коррелируют со случайными возмущениями в предыдущих наблюдениях: COV(xi,ui)=0, CОV(xi,ui-1)≠0 (Оценки смещенные на небольших выборках и состоятельные на выборках большого объема)
3. Регрессоры коррелируют со случайными возмущениями в текущих уравнениях наблюдений: СOV(xi,ui)≠0 (Оценки смещенные и несостоятельные)

Модели со стохастическими регрессорами
Рассмотрим модель вида:
Система уравнений наблюдений для модели (1.1)
(1.1)
(1.2)
Лаговая переменная yt-1 коррелирует со случайным возмущением в предыдущих наблюдениях
Модель (1.1) частный случай авторегрессионных моделей

Модели с распределенными лагами
2. Модели с конечным числом лагов
(2.1)
Решается методом замены переменных
Вводятся новые переменные: z0t=xt, z1t=xt-1,…,zkt=xt-k
В новых переменных получается обычное уравнение множественной регрессии
Его оценка и анализ производится с помощью МНК

Модели с распределенными лагами
3. Модели с бесконечным числом лагов
В общем случае они имеют вид:
(3.1)
Предпосылка: параметры bi при лаговых значениях регрессоров убывают в геометрической прогрессии: bk=b0λk, k=0,1,…, 0<λ<1
Параметр λ характеризует скорость убывания коэффициентов с увеличением лага

Модели с распределенными лагами
Метод оценки модели (3.2) – метод переход к модели с конечным лагом:
Задают набор значений параметра λ, например, (0.1, 0.001, 0.0001)
2. Для каждого λ рассчитывается значение переменной
Модель (3.1) принимает вид:
(3.2)
Значение максимального лага «р» подбирается из условия

3. Методом наименьших квадратов оценивается модель:
Для каждого λ получают значения оценок a0 и bo
Из набора значений параметра λ выбирается то, при котором коэффициент детерминации R2 имеет максимальное значение
4. Найденное значение λ и соответствующие ему значения параметров a0 и b0 используются в модели (3.2)
Модели с распределенными лагами

Модели частичной корректировки
В экономической практике часто приходится моделировать не фактические значения эндогенной переменной, а ее ожидаемое или целевое значение
Например, ожидаемый доход от ценных бумаг, инвестиций, ожидаемый уровень дивидендов и т.п.)
Пусть yt – фактическое значение эндогенной переменной
y*t – ожидаемое значение эндогенной переменной
xt – экзогенная переменная
Необходимо построить модель:
(4.1)

Особенность: отсутствие данных по переменной y*t
Делается предположение, что фактическое приращение эндогенной переменной пропорционально разности между ее желаемым уровнем и реальным значением в прошлом периоде:
(4.2)
Выражение (4.2) можно переписать в виде:
yt – средневзвешенное желаемого уровня эндогенной переменной и фактическим ее значением в предыдущем периоде
(4.3)
Модели частичной корректировки

Подставив (4.1) в (4.3) получим выражение:
(4.4)
Оценив параметры модели (4.4), получим оценки всех необходимых параметров: λ, а0 и а1
Однако модель (4.4) имеет стохастический регрессор yt-1, что приводит к «частичному» нарушению четвертой предпосылки теоремы Гаусса-Маркова
Поэтому оценку модели (4.4) необходимо проводить по выборке большого объема.
Модели частичной корректировки

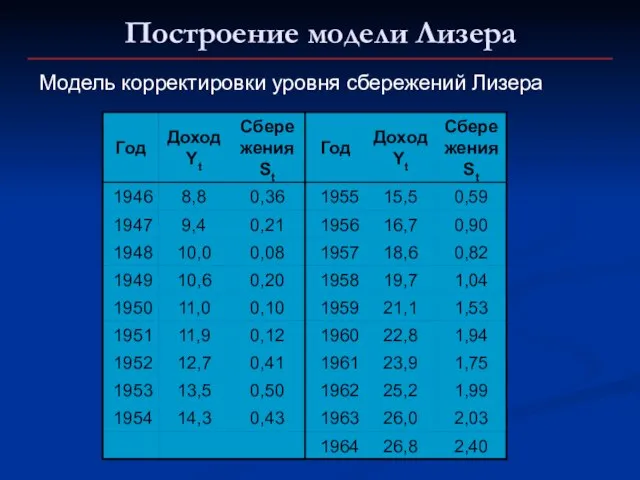
Построение модели Лизера
Модель корректировки уровня сбережений Лизера

Построение модели Лизера
Спецификация модели
где: S*t –ожидаемый уровень сбережений в текущем году
Используется предположение:
(4.5)
(4.6)
Подставляя (4.5) в (4.6) после преобразования получим
(4.7)

Построение модели Лизера
Вводя новые значения параметров:
(4.8)
спецификация (4.7) принимает вид:
(4.9)
Оценка спецификации (4.9) по имеющимся данным
Возвращаемся к исходным параметрам согласно (4.8)

Модели адаптивных ожиданий
Случай «противоположный» рассмотренному
Например. Известно, что дивиденды от ценной бумаги 30% в год от ее стоимости. Но не известно, какова будет ее стоимость в следующем периоде времени
Инвестор ориентируется на некоторое ожидаемое значение в будущем
Спецификация модели имеет вид:
(5.1)
где: X*t-1 – ожидаемое значение регрессора в следующем периоде времени

Модели адаптивных ожиданий
Т.к. X*t-1 величина не наблюдаемая, ее заменяют на ту переменную, которая поддается наблюдениям
В данном случае – это текущее значение регрессора
Предполагается, что ожидаемое значение регрессора есть взвешенное среднее между текущими реальным и ожидаемым значениям регрессора:
Другими словами, предполагается:
(5.2)