Слайд 2Задача.
Построить математическую модель физического процесса — движения тела, брошенного под углом к

горизонту.
Выяснить зависимость расстояния и времени полета тела от угла броска и начальной скорости.
Угол броска и начальная скорость являются главными факторами процесса моделирования.
Слайд 3Решение.
Постановка задачи.
При расчетах будем использовать следующие допущения:
начало системы координат расположено

в точке бросания;
тело движется вблизи поверхности Земли, т. е. ускорение свободного падения постоянно и равно 9,81 м/с²;
сопротивление воздуха не учитывается, поэтому движение по горизонтали равномерное.
Слайд 4Пусть
Vo — начальная скорость (м/с),
α — угол бросания (радиан),
L —
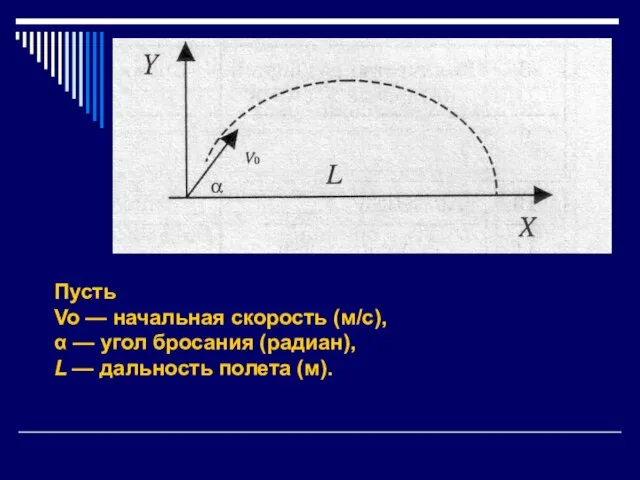
дальность полета (м).
Слайд 5Движение тела, брошенного под углом к горизонту, описывается следующими формулами:
Vx = Vo

cos α — горизонтальная составляющая начальной скорости,
Vy = Vx sin α — вертикальная составляющая начальной скорости,
х = Vx t — так как движение по горизонтали равномерное,
Слайд 6у = Vy t - – так как движение по
вертикали равноускоренное

с
отрицательным ускорением.
Искомым в этой задаче будет то
значение х = L, при котором у = 0.
Слайд 7Математическая модель.
Дано:
Vo — начальная скорость (м/с),
α — угол бросания (радиан).
Найти:
L

— дальность полета (м).
Слайд 8Связь:
(1) L = Vx t - — дальность полета,
(2) 0 = Vy

t – — точка падения,
(3) Vx = Vo cos α — горизонтальная проекция вектора начальной скорости,
(4) Vy = Vo sin α — вертикальная проекция вектора начальной скорости,
g = 9,81 — ускорение свободного падения,
Vo > 0
0 < α < .
Слайд 9Подставляем в формулу (2)
значение Vy из формулы (4).
Получаем уравнение:
(5)

Слайд 10Чтобы решить это уравнение, найдем из формул (1) и (3) выражение для

t:
Слайд 11Подставив это значение в уравнение (5), получаем решение:

Слайд 12или
Отсюда дальность полета равна:
т. е. зависит от начальной скорости и угла наклона.

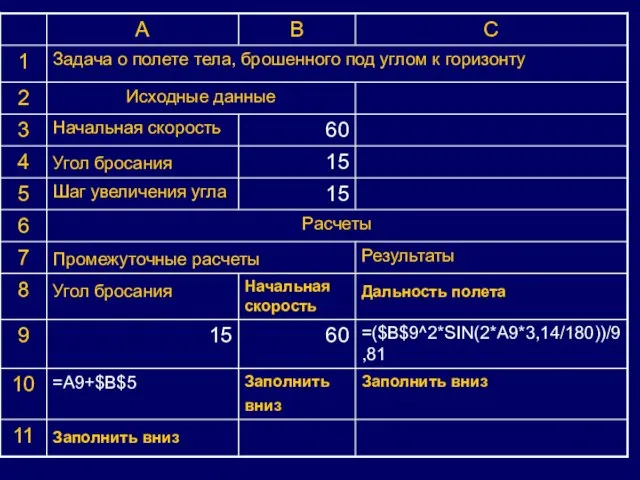
Слайд 13Компьютерный эксперимент.
I. Выяснить, как зависит дальность
полета от угла броска.
(Используем Excel)
В формульном

виде:
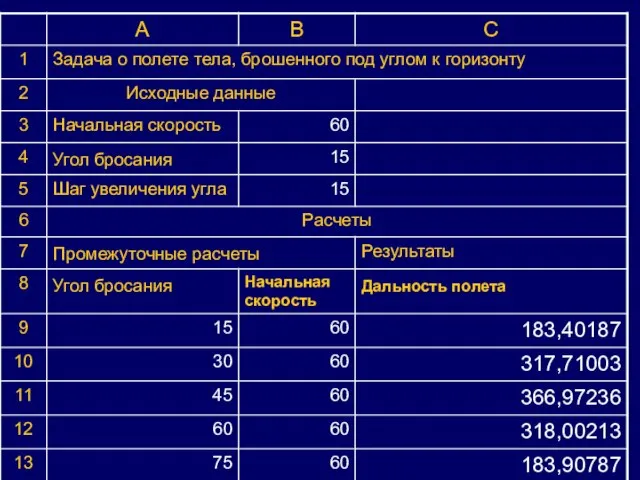
Слайд 16Делаем выводы:
С увеличением угла бросания от 15 до 45° при постоянной начальной

скорости полета дальность полета увеличивается.
С увеличением угла бросания от 45 до 90° при постоянной начальной скорости полета дальность полета уменьшается.
Слайд 172. Выяснить, как зависит на Луне дальность полета от угла броска (g

= 1,63 м/с²)














 И.С.Тургенев: жизнь и творчество
И.С.Тургенев: жизнь и творчество Начальные годы создания Русского государства — Киевской Руси — можно соотнести с 862-882 гг.
Начальные годы создания Русского государства — Киевской Руси — можно соотнести с 862-882 гг. Учебно-методический пакет Здравствуй, лес, дремучий лес, Полный сказок и чудес!
Учебно-методический пакет Здравствуй, лес, дремучий лес, Полный сказок и чудес!  Реле переменного тока. Реле выдержки времени
Реле переменного тока. Реле выдержки времени Ипотечные ценные бумаги: перспективное направление развития рынка коллективных инвестиций.
Ипотечные ценные бумаги: перспективное направление развития рынка коллективных инвестиций. 20140928_prilozhenie
20140928_prilozhenie Анализ и качество автомобильной аудиотехники, реализуемой в торговом предприятии М-Видео
Анализ и качество автомобильной аудиотехники, реализуемой в торговом предприятии М-Видео Воронцова Елена Геннадьевна учитель русского языка и литературы Высшей квалификационной категории МОУ «Сиверская СОШ №3»
Воронцова Елена Геннадьевна учитель русского языка и литературы Высшей квалификационной категории МОУ «Сиверская СОШ №3» Государственный Эрмитаж
Государственный Эрмитаж Картограмма доступности маршрутной сети
Картограмма доступности маршрутной сети 2011 Год Италии в России
2011 Год Италии в России Презентация на тему Салтыков-Щедрин "Сказки"
Презентация на тему Салтыков-Щедрин "Сказки" Проект подготовлен учащейся І-А курса Чейлях Мариной.
Проект подготовлен учащейся І-А курса Чейлях Мариной. Как встречают Новый Год люди всех земных широт. История главного праздника в разных странах
Как встречают Новый Год люди всех земных широт. История главного праздника в разных странах Финансовый клуб ВШМ. Карьерные пути в финансах, введение в Investment Banking
Финансовый клуб ВШМ. Карьерные пути в финансах, введение в Investment Banking Бюджетирование, ориентированное на результат (БОР), и программно-целевые методы бюджетного планирования
Бюджетирование, ориентированное на результат (БОР), и программно-целевые методы бюджетного планирования Подчинительная связь слов в словосочетании
Подчинительная связь слов в словосочетании Искусственные Спутники Земли
Искусственные Спутники Земли Северный модерн
Северный модерн Типовые технологические процессы изготовления готовой продукции
Типовые технологические процессы изготовления готовой продукции Ландшафтный дизайн участка
Ландшафтный дизайн участка Годовой отчет группы Звездочка за 2020-21 уч. год
Годовой отчет группы Звездочка за 2020-21 уч. год Возможности человека
Возможности человека Презентация на тему Переход прилагательных в существительные
Презентация на тему Переход прилагательных в существительные Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для банков и кредитно-финансовых организаций СТАНДАРТ С
Cisco Solution Technology Integrator Сетевая безопасность для вертикальных рынков Решения для банков и кредитно-финансовых организаций СТАНДАРТ С Колебания и волны
Колебания и волны Презентация на тему Радиация и её воздействие на человека
Презентация на тему Радиация и её воздействие на человека  Отчет о деятельности за 2011 год
Отчет о деятельности за 2011 год