Моделирование контентных сетей

Complex Networks
В настоящее время наряду с традиционным
теориями графов, систем и сетей массового обслуживания активно развивается теория сложных сетей (от англ. – Complex Networks), в рамках которой предлагаются подходы к решению вычислительно сложных задач, характерных для современных сетей.
Основной причиной актуальности теории сложных сетей являются результаты современных работ по описанию реальных компьютерных, биологических и социальных сетей. Cвойства многих реальных сетей существенно отличаются от свойств классических случайных графов с равновероятной связностью узлов, а строятся на основе связных структур, степенных распределений. .

Основы концепции
Практически все современные сети можно считать сложными. Так, например, известная задача синтеза топологии сети допускает комбинаторный подход, опирающийся на представление сети в виде конечного графа, вершины которого соответствуют узлам сети,
а ребра – линиям связи.
Например, в сети из 10 узлов существует 245 вариантов размещения линий связи (для 10 узлов теоретически возможно С210 линий соединений. Каждая из этих возможных линий связи может реально существовать – состояние «1», или не существовать – состояние «0», то есть всего возможностей ).
Варианты размещения
линий связи при n=3

Направления теории сложных сетей
В теории сложных сетей выделяют три основных направления:
- исследование статистических свойств, которые характеризуют поведение сетей;
- создание модели сетей;
- предсказание поведения сетей при изменении структурных свойств.

Параметры сложных сетей
В прикладных исследованиях обычно применяют такие типичные для сетевого
анализа характеристики, как размер сети, сетевая плотность, степень центральности и т.п.
При анализе сложных сетей как и в теории графов исследуются параметры отдельных узлов; параметры сети в целом; параметры сетевых подструктур.

Параметры узлов сети
Выделяют следующие параметры:
входная степень связности узла – количество
ребер, которые входят в узел;
- выходная степень связности узла – количество ребер, которые выходят из узла;
- расстояние от данного узла до каждого из других;
- среднее расстояние от данного узла до других;
- эксцентричность – наибольшее из геодезических расстояний от данного узла к другим;
- посредничество - показывающее, сколько кратчайших путей проходит через данный узел;
- центральность – общее количество связей данного узла по отношению к другим;
- уязвимость, рассматриваемая как уровень спада “проводимости» сети в случае удаления вершины и всех смежных ей ребер.

Общие параметры сети
Наиболее часто используются такие параметры:
количество узлов, число ребер, среднее расстояние
от одного узла к другим, плотность – отношение
количества ребер в сети к макс. возможному количеству, количество симметричных, транзитивных и циклических
триад, диаметр - максимальная уязвимость всех вершин сети, ассортативность - мера зависимости между узлами с одинаковыми степенями…
Существует несколько задач исследования сложных сетей, среди которых можно выделить следующие основные: определение клик, кластеров, в которых узлы связаны между собой сильнее, чем с членами других подобных фрагментов; выделение компонент связности, которые связаны внутри и не связаны
между собой; нахождение перемычек, т.е. узлов, при изъятии которых сеть распадается на несвязанные части.

Распределение степеней
связности узлов
Важной характеристикой сети является функция распределения степеней узлов P(k), которая
определяется как вероятность того, что узел i имеет степень ki = k. Распределение степеней P(k) отражает долю вершин со степенью k.
Для ориентированных сетей существует распределение выходящей полустепени Pout(kout), и полустепени входной Pin(kin), а также распределение общей степени Pio(kin,kout).
P(k) в некоторых случаях может быть распределениями Пуассона (P(k)=e-mmk/k! , где m – математическое ожидание), экспоненциальным (P(k)=e-k/m) или степенным ( P(k)=1/kγ).

Путь между узлами
Если два узла i и j можно соединить с помощью последовательности из m ребер, то такую последовательность называют маршрутом (walk) между узлами i и j, а m называю длиной маршрута.
Расстояние между узлами определяется как длина маршрута от одного узла до другого. Естественно, узлы могут быть соединены прямо или опосредованно. Путем между узлами dij называется кратчайшее расстояние между ними. Для всей сети можно ввести понятие среднего пути, как среднее по всем парам узлов кратчайшего расстояния между ними:

Глобальная эффективность
Некоторые сети могут оказаться несвязными. Соответственно, средний путь может оказаться также равным бесконечности. Для таких случаев вводится
понятие глобальной эффективности сети, рассчитываемое по формуле:
где сумма учитывает все пары узлов. Эта характеристика отражает эффективность сети при пересылке информации между узлами (предполагается, что эффективность в пересылке информации между двумя узлами и обратно пропорциональна расстоянию между ними).
Обратная величина глобальной эффективности – среднее гармоническое геодезических расстояний:
h=1/E.
.

Коэффициент кластеризации
Дункан Уаттс и Стив Строгатц определили
коэффициент кластерности, который Данный
Коэффициент характеризует тенденцию к образованию групп взаимосвязанных узлов, так называемых клик
(clіque). Пусть из узла выходит k ребер, которые
соединяют его с k другими узлами, ближайшими соседями. Если предположить, что все ближайшие соседи соединены непосредственно друг с другом, то количество ребер между ними составляло бы k(k-1)/2. Т.е. это число, которое соответствует максимально возможному количеству ребер, которыми могли бы соединяться ближайшие соседи выбранного узла. Отношение реального количества ребер, которые соединяют ближайших соседей данного узла к максимально возможному (такому, при котором все ближайшие соседи данного узла были бы соединены непосредственно друг с другом) называется коэффициентом кластеризации узла.
Watts

Сложные сети и задачи компьютерной лингвистики
Первым шагом при применении теории сложных сетей к анализу текста является представление
этого текста в виде совокупностиузлов и связей,
построение сети языка (language network).
Существуют различные способы интерпретации узлов и связей, что приводит, соответственно, к различным представлениям сети языка.
Узлы могут быть соединенны меду собой, если соответствующие им слова стоят рядом в тексте, принадлежат одному предложению, соединены синтаксически или семантически. Сохранение синтаксических связей между словами приводит к изображению текста в виде направленной сети (dіrected network), где направление связи соответствует подчинению слова.

Простейшие типы сетей в лингвистике
L-пространство. Связываются соседние слова, которые принадлежат одному предложению. Количество соседей для каждого слова (окно слова) определяется радиусом взаимодействия R, чаще
всего рассматривается случай R = 1.
B-пространство. Рассматриваются узлы двух видов, соответствующие предложениям и словам, которые им принадлежат.
P-пространство. Все слова, которые принадлежат одному предложению, связываются между собой.
C-пространство. Предложения связываются между собой, если в них употреблены одинаковые слова.

Экспериментальные данные
В случае рассмотрения L-пространства языка количество соседних слов, между которыми строятся связи, определяется параметром R: при R= 1 связаны между собой лишь ближайшие соседи, при R= 2 связи строятся между узлом-словом, его ближайшими и предшествующими близкими соседями и т. д.
Для сети, построенной на основании Британского национального корпуса, оказалось, что данная сеть английского языка безмасштабна, а поведение степени P(k) характеризуется двумя режимами степенного распределения со значением степенного показателя γ=1.5 для k<2000 и γ=2.7 для k> 2000 соответственно.
Согласно определению, если средняя длина кратчайшего пути растет количеством узлов сети медленнее любой функции степени, то сеть является «малым миром». Данная сеть оказалась именно такой.

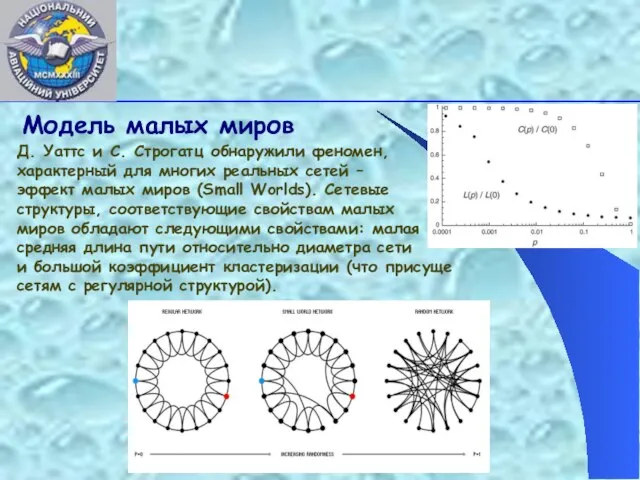
Модель малых миров
Д. Уаттс и С. Строгатц обнаружили феномен, характерный для многих реальных сетей –
эффект малых миров (Small Worlds). Сетевые структуры, соответствующие свойствам малых
миров обладают следующими свойствами: малая средняя длина пути относительно диаметра сети
и большой коэффициент кластеризации (что присуще сетям с регулярной структурой).

Модель случайной сети Эрдоша-Рени
Существует две модели классического случайного графа: в первой считается, что M ребер распределены произвольно и независимо между парами из N вершин графа; во второй модели фиксируется вероятность m, с которой может объединяться каждая из пар врешин. При m -> ∞ и N -> ∞ для обоих вариантов распределение степеней узлов k определяется формулой Пуассона:
где среднее значение степени узла:
=2M/N для первой модели и
=mN для второй. При этом средняя длина кратчайшего пути для сети Эрдоша-Рени составляет
=ln(N)/ln(
), а коэффициент кластерности: C~
/N.

Модель случайной сети Барабаши-Альберта
Сценарий базируется на двух механизмах – росте и преимущественном присоединении (preferentіal attachment). Mодель использует алгоритм: рост сети происходит начиная с небольшого количества узлов n0, к которым на каждом временном шагу добавляется новый узел с n < n0 связями, которые присоединяются к уже существующим узлам; преимущественное присоединение состоит в том, что вероятность присоединения P(ki) нового узла к уже существующему узлу i зависти от степени ki узла i:

Сложные сети с заданным распределением
формируется степенная последовательность,
выбирая N чисел ki согласно заданному
распределению;
- каждой вершине i графа присваивается ki «заготовок» (концов) для будущих ребер;
- из степенной последовательности случайно извлекаются пары «заготовок». Они соединяются ребром в том случае, если новое ребро не приведет к появлению ребер-циклов (петель) или мультиребер. Если ребро сгенерировано, то соответствующие индексы из степенной последовательности удаляются;
- предыдущий шаг повторяется до тех пор, пока степенная последовательность не пуста.

Алгоритм построения контентной сети
Алгоритм Барабаши-Альберта позволяет
генерировать сети со степенным распределением, однако эти сети слишком формальны, в них нет содержательной составляющей.
Для построения модели сети с параметрами, близкими к тем, которые наблюдаются в веб-пространстве, предлагается рассмотреть следующую архитектуру сети. Пусть сеть состоит из N узлов.
Пусть есть i-й узел (аналог веб-сайта). Пусть узел содержит документов (веб-страниц). Каждый документ имеет свой поисковый образ – вектор из весов термов (ключевых слов), входящих в него, m – объем тезауруса (словаря).

Распределения в модели
Изначально предполагается, что распределение количества документов по узлам – степенное
(аналог – распределение богатства – закон Парето). Распределение ключевых слов в документах – также степенное (аналог – распределение слов в текстах – закон Ципфа). В качестве направленных ребер сети рассматриваются гиперссылки между узлами. Предполагается, что количество входящих в узел ребер пропорционально количеству документов, принадлежащих ему. Также предполагается, что распределение степеней узлов сети – как и в случае веб-пространства степенное.

Основные шаги алгоритма
1. Выбирается количество узлов сети N;
2. Для каждого узла генерируется число, соответствующее количеству документов– его объем;
3. Для каждого документа генерируется вектор ключевых слов;
4. Для каждого узла генерируются его входная и выходная степени, приблизительно пропорциональные его объему. Степени узлов заранее распределяются по степенному закону;
5. Для каждого узла рассчитывается центроид;
6. Вычисляется матрица близости между документами на основании близости центроидов;
7. Циклично, начиная с узла с наибольшей входной степенью, случайным образом устанавливаются ребра от свободных выходных концов других узлов к свободным входным концам данного узла.

Преимущества модели
1. Ориентация на контент документов при
установлении связей (построении ребер);
2. При построении сети учитываются вполне
реальные предпосылки (чем больше узел, тем больше ссылок устанавливается на него, преимущественно устанавливаются связи близкими по содержанию узлами, учитывается реалистическое распределение количества документов между узлами и ключевых слов в документах);
3. В построенной сети, оказалось, что такой показатель, как PageRank имеет решающее значение при организации содержательного поиска в сети.

Решаемые задачи
Полученная в результате моделирования сеть, обладает многими параметрами, близкими к
реальной сети, что по-видимому, позволит
решать некоторые задачи, обуславливающие моделирование сетей близких к реальным, а
именно:
- выявления новых закономерностей и феноменов;
- изучение природы формирования/развития отдельных сетей;
- моделирование процессов передачи информации в сетях;
- моделирование задач заражения/иммунизации;
- противодействия сетевым атакам;
- решения задач навигации (поиска) в сетевых структурах и т.п.