Содержание
- 2. Величина Характеристики величины: имя, тип, значение Функциональные и иные виды зависимостей Математические модели Табличные и графические
- 3. Применение математического моделирования Примеры зависимостей: время падения тела на землю зависит от его первоначальной высоты; давление
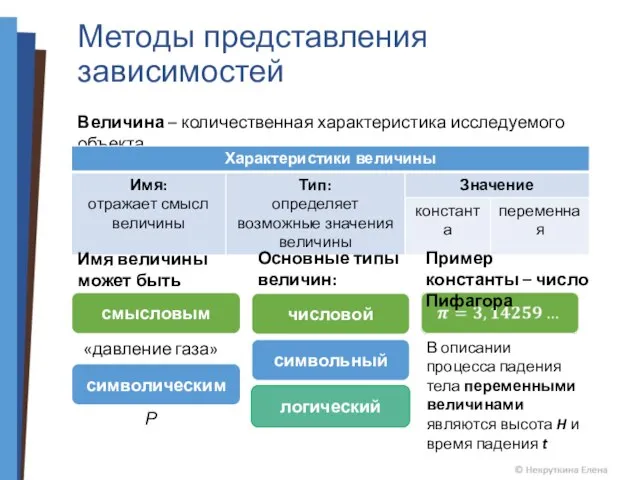
- 4. Методы представления зависимостей Величина – количественная характеристика исследуемого объекта Имя величины может быть смысловым символическим «давление
- 5. Виды зависимостей Функциональной зависимостью называется связь между двумя величинами, при которой изменение одной из них вызывает
- 6. Виды зависимостей Иная зависимость носит более сложный характер, одна и та же величина может принять разные
- 7. Математические модели Математические модели — это совокупность количественных характеристик некоторого объекта (процесса) и связей между ними,
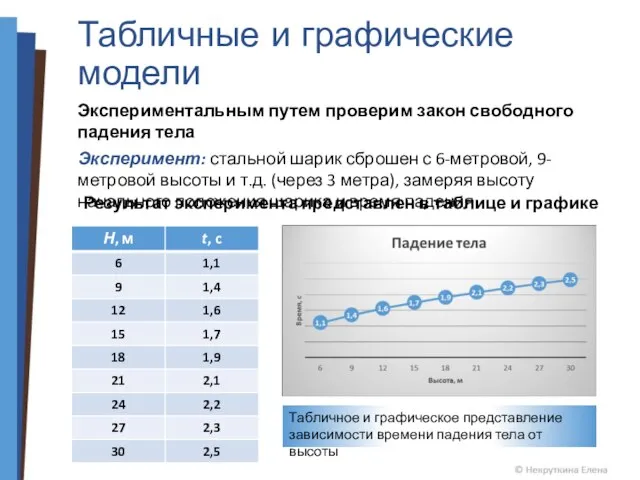
- 8. Табличные и графические модели Экспериментальным путем проверим закон свободного падения тела Эксперимент: стальной шарик сброшен с
- 9. Динамические модели Информационные модели, которые описывают развитие систем во времени, имеют специальное название: динамические модели. В
- 10. Самое основное Величина – количественная характеристика исследуемого объекта. Характеристики величины: Имя – отражает смысл величины Тип
- 11. Вопросы и задания Какие вам известны формы представления зависимостей между величинами? Что такое математическая модель? Может
- 13. Скачать презентацию








 Материалы для дистанционной поддержки учащихся по дополнительной программе Шахматы для начинающих
Материалы для дистанционной поддержки учащихся по дополнительной программе Шахматы для начинающих Основы построения телекоммуникационных систем и сетей Лекция №7 «Сеть следующего поколения» профессор Соколов Н.А.
Основы построения телекоммуникационных систем и сетей Лекция №7 «Сеть следующего поколения» профессор Соколов Н.А. 16 ноября 2007 г. Николай Димченко Управляющий директор Долговое агентство «Пристав» Управление проблемными активами – современный
16 ноября 2007 г. Николай Димченко Управляющий директор Долговое агентство «Пристав» Управление проблемными активами – современный  Компьютер в жизни подростка
Компьютер в жизни подростка АНАЛИЗ РАБОТЫ ШКОЛЫ ЗА 2010-2011 УЧЕБНЫЙ ГОД
АНАЛИЗ РАБОТЫ ШКОЛЫ ЗА 2010-2011 УЧЕБНЫЙ ГОД Презентация на тему: Помоги ёжику
Презентация на тему: Помоги ёжику Изготовление платья. Внесение изменений .Обработка рюш, настрачивание рюш на полочки
Изготовление платья. Внесение изменений .Обработка рюш, настрачивание рюш на полочки Новеллы в законодательстве о контрактной системе в сфере закупок товаров, работ и услуг для государственных нужд
Новеллы в законодательстве о контрактной системе в сфере закупок товаров, работ и услуг для государственных нужд Сила трения. Трения в природе и технике
Сила трения. Трения в природе и технике Прошу дождя
Прошу дождя Формы организации внеурочной деятельности в условиях введения ФГОС НОО
Формы организации внеурочной деятельности в условиях введения ФГОС НОО Цветы
Цветы Взаимодействие HR и руководителей производственных подразделений
Взаимодействие HR и руководителей производственных подразделений Библиотека
Библиотека конфигурация по расчету квартплаты в Украине
конфигурация по расчету квартплаты в Украине Республика Казахстан Министерство образования и науки РК Внедрение фостерной заботы:опыт, извлеченные уроки
Республика Казахстан Министерство образования и науки РК Внедрение фостерной заботы:опыт, извлеченные уроки Рецидивная преступность
Рецидивная преступность Слитное и раздельное написание НЕ с наречиями на - О и -Е
Слитное и раздельное написание НЕ с наречиями на - О и -Е Песколовки
Песколовки Общая фармакология
Общая фармакология  Теоретические основы маркетинга
Теоретические основы маркетинга Новый уровень энергосбережения, безопасности и комфорта
Новый уровень энергосбережения, безопасности и комфорта Администрация городского округа Самара Автономное муниципальное образовательное учреждение высшего профессионального образова
Администрация городского округа Самара Автономное муниципальное образовательное учреждение высшего профессионального образова Влияние внутренней обратной связи на свойства резонансного усилителя
Влияние внутренней обратной связи на свойства резонансного усилителя Лекция №1Становление и развитие компьютерных систем автоматизации
Лекция №1Становление и развитие компьютерных систем автоматизации «Международное сотрудничество в сфере уголовного судопроизводства »
«Международное сотрудничество в сфере уголовного судопроизводства » Итальянский стиль в интерьере
Итальянский стиль в интерьере Воспитателя детского сада
Воспитателя детского сада