Содержание
- 2. Случайное явление (событие) – это такое явление, которое при неоднократном воспроизведении одного и того же эксперимента
- 3. Осуществление каждого отдельного наблюдения (измерения) при изучении эксперимента называют испытанием. Результат испытания называется событием. Достоверное событие
- 4. Вероятностью события называют отношение числа m благоприятствующих этому событию исходов к общему числу n всех возможных
- 5. Последовательность случайных событий можно получить с помощью генератора случайных чисел. Недостатки: необходимо специальное устройство; невозможно воспроизвести
- 6. Датчики случайных чисел – компьютерные программы, моделирующие работу генераторов случайных чисел. Псевдослучайные числа – обладают свойствами
- 7. Линейный конгруэнтный метод a, c, m – целые числа. Период = m «Вихрь Мерсенна» - генератор
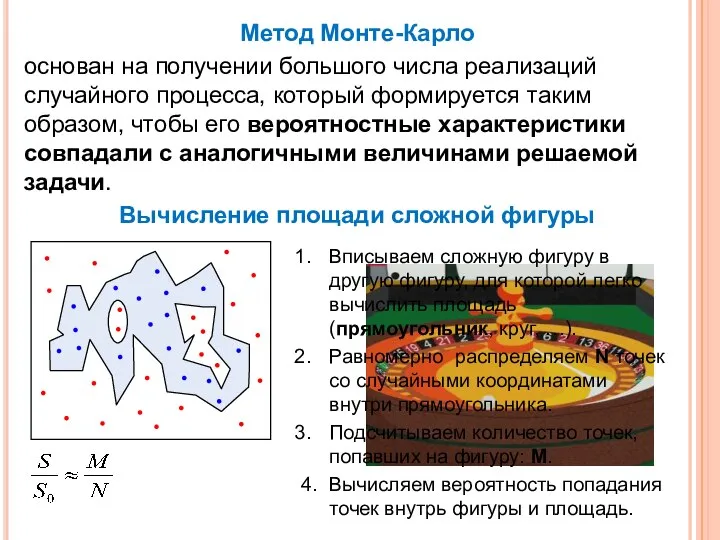
- 8. Метод Монте-Карло основан на получении большого числа реализаций случайного процесса, который формируется таким образом, чтобы его
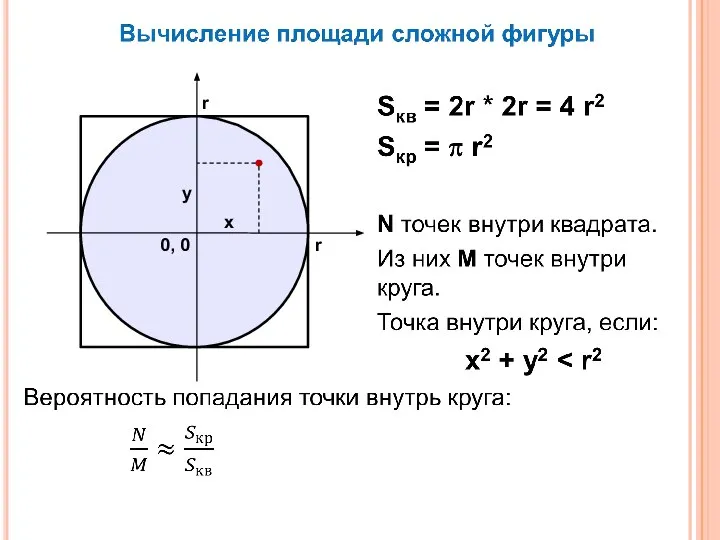
- 9. r r 0, 0 x y
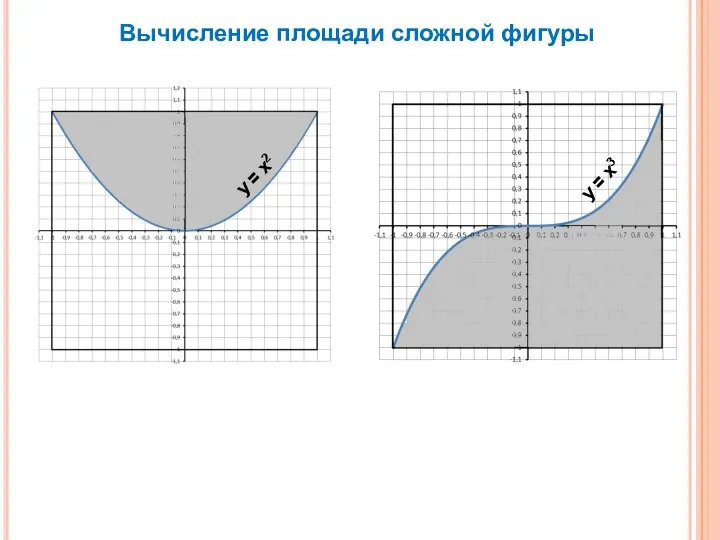
- 10. Вычисление площади сложной фигуры
- 12. Скачать презентацию






 Лучший способ сделать детей хорошими – это сделать их счастливыми
Лучший способ сделать детей хорошими – это сделать их счастливыми Презентация на тему Cилы и средства ликвидации чрезвычайных ситуаций
Презентация на тему Cилы и средства ликвидации чрезвычайных ситуаций  Мудрые советы Лао Цзюня
Мудрые советы Лао Цзюня Новые функциональные возможности «1С:Управление торговлей 8» для решения оперативных задач специалистами торговых предприятий
Новые функциональные возможности «1С:Управление торговлей 8» для решения оперативных задач специалистами торговых предприятий ЧТО ТАКОЕ IELTS? www.studybady.comwww.studybady.com – полезная информация об обучении в Великобритании и получении студенческой визы www.studybady.comwww.studyba
ЧТО ТАКОЕ IELTS? www.studybady.comwww.studybady.com – полезная информация об обучении в Великобритании и получении студенческой визы www.studybady.comwww.studyba Наш друг компьютер
Наш друг компьютер Комплекс упражнений утренней гимнастики (1 класс)
Комплекс упражнений утренней гимнастики (1 класс) Личность и политик
Личность и политик «Времена не выбирают: в них живут и умирают…»
«Времена не выбирают: в них живут и умирают…» Целевой проектСпособный ребёнок
Целевой проектСпособный ребёнок Introduction to Management
Introduction to Management 23.04. uneployment
23.04. uneployment Е. Поплянова «Начинается урок»
Е. Поплянова «Начинается урок» Презентация на тему Роль учителя в современной школе
Презентация на тему Роль учителя в современной школе  Саргатская культурно- историческая общность
Саргатская культурно- историческая общность Гимнастика
Гимнастика портфолио воспитателя
портфолио воспитателя Национальные символы России
Национальные символы России Рейтинг застройщиков
Рейтинг застройщиков Буддизм
Буддизм Лаборатория 711, 713, 715. Планы. Долги
Лаборатория 711, 713, 715. Планы. Долги Презентация на тему Вторая война Рима с Карфагеном
Презентация на тему Вторая война Рима с Карфагеном  Ассортимент
Ассортимент Урок развития речи в 7 классеКомплексный анализ текста ”Памятник подлецу”
Урок развития речи в 7 классеКомплексный анализ текста ”Памятник подлецу” В стране веселого детства
В стране веселого детства Презентация на тему Наука и образование в Древней Греции
Презентация на тему Наука и образование в Древней Греции Роль имени прилагательного в речи.
Роль имени прилагательного в речи. Где обитают знаки препинания?
Где обитают знаки препинания?