Содержание
Слайд 21. Определение произведения вектора на число
Произведение ненулевого вектора a и числа k
1. Определение произведения вектора на число
Произведение ненулевого вектора a и числа k

– это такой вектор b, длина которого равна |k|⋅|а|, причём:
a ↑↑ b, если k ≥ 0
а ↑↓b, если k < 0.
a ↑↑ b, если k ≥ 0
а ↑↓b, если k < 0.
Слайд 3Дано:
a; b
т. А
Построить:
0,5a – 2b
В
С
Доказательство:
0,5a = АВ (а↑↑АВ, |0,5a| = |AB|)
Дано:
a; b
т. А
Построить:
0,5a – 2b
В
С
Доказательство:
0,5a = АВ (а↑↑АВ, |0,5a| = |AB|)
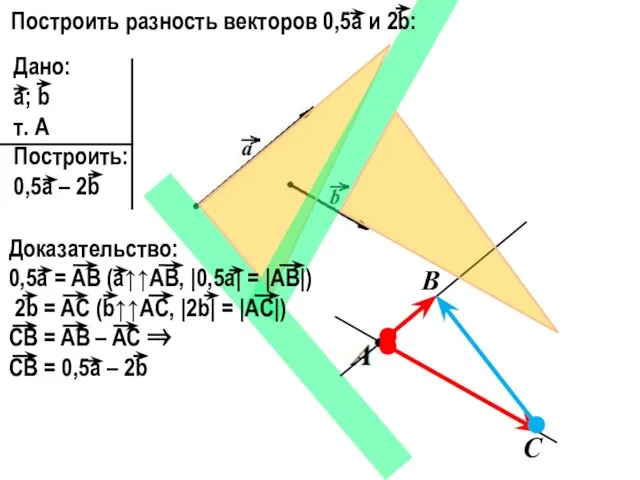
2b = AC (b↑↑AC, |2b| = |AC|)
CB = AB – AC ⇒
CB = 0,5a – 2b
CB = AB – AC ⇒
CB = 0,5a – 2b
 Красота в деталях: искусство Древнего Китая. 7 класс
Красота в деталях: искусство Древнего Китая. 7 класс Пензенский выездной детский драматический театр
Пензенский выездной детский драматический театр Исторический путь СССР 1922 – 1941 гг
Исторический путь СССР 1922 – 1941 гг Инновационное развитие и информационно – коммуникационные технологии: новые механизмы и государственно – частное партнерство (
Инновационное развитие и информационно – коммуникационные технологии: новые механизмы и государственно – частное партнерство ( Транспорт, его развитие и состав. Экологические проблемы и перспективы развития транспорта Беларуси
Транспорт, его развитие и состав. Экологические проблемы и перспективы развития транспорта Беларуси Лекция 1. Введение в веб-психологию: актуальность и история становления
Лекция 1. Введение в веб-психологию: актуальность и история становления Falling Walls Lab – это международная блиц-конференция на английском языке
Falling Walls Lab – это международная блиц-конференция на английском языке Производные финансовые инструменты: новые идеи в маркетинге и управлении активами
Производные финансовые инструменты: новые идеи в маркетинге и управлении активами Тундра (4 класс)
Тундра (4 класс) Some and any
Some and any Sketch for design
Sketch for design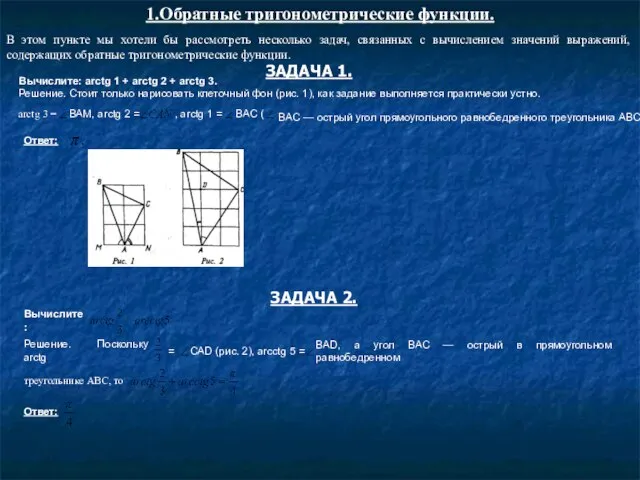 1.Обратные тригонометрические функции.
1.Обратные тригонометрические функции. Тема: “Прямоугольный параллелепипед.”
Тема: “Прямоугольный параллелепипед.” Объекты розничной торговли
Объекты розничной торговли Презентация на тему Революция 1905-1907 годов
Презентация на тему Революция 1905-1907 годов  Контрольные работы и стресс
Контрольные работы и стресс Администратор Штаба
Администратор Штаба Обучающее изложение Купание медвежат 4 класс
Обучающее изложение Купание медвежат 4 класс Проект программы развития гимназии на 2011-2016гг.
Проект программы развития гимназии на 2011-2016гг. Перпендикулярность
Перпендикулярность Приоритетные научные проблемы в области природной безопасности
Приоритетные научные проблемы в области природной безопасности МОО Диалог
МОО Диалог Подготовка к сдаче отчета за 2011 год по финансово-статистической форме № 62 «Сведения об оказании и финансировании медицинской пом
Подготовка к сдаче отчета за 2011 год по финансово-статистической форме № 62 «Сведения об оказании и финансировании медицинской пом Полномочия администрации. Панковского городского поселения Бюджет. Панковского городского поселения
Полномочия администрации. Панковского городского поселения Бюджет. Панковского городского поселения Социально-экономическое развитие Северо-Кавказского федерального округа в январе-сентябре 2011 года
Социально-экономическое развитие Северо-Кавказского федерального округа в январе-сентябре 2011 года Шпа Музыкальная интуиция
Шпа Музыкальная интуиция Никто не умеет баловать, так как мамочка
Никто не умеет баловать, так как мамочка Управление человеческими ресурсами
Управление человеческими ресурсами