МОСТ ЧЕРЕЗ РЕКУ:

ТЕОРИЯ:
ЦЕНТРАЛЬНАЯ
СИММЕТРИЯ
ОСЕВАЯ
СИММЕТРИЯ
ПАРАЛЛЕЛЬНЫЙ
ПЕРЕНОС
ПОВОРОТ
ВОКРУГ ТОЧКИ
ДВИЖЕНИЕ

ТЕОРИЯ:
ПАРАЛЛЕЛЬНЫМ ПЕРЕНОСОМ ПЛОСКОСТИ НА ВЕКТОР а
а
Х1=Х+а
У1=У+в,
где (а;в) координаты вектора
а
НАЗЫВАЕТСЯ ТАКОЕ ПРЕОБРАЗОВАНИЕ ПЛОСКОСТИ,
ПРИ КОТОРОМ ЛЮБОЙ ТОЧКЕ М (х, у) СООТВЕТСТВУЕТ ТАКАЯ ТОЧКА М1 (х1, у1), ЧТО ММ1=а
и задается формулой

ЗАПОЛНИТЕ ПРОПУСКИ, ЧТОБЫ ПОЛУЧИЛОСЬ ВЕРНОЕ УТВЕРЖДЕНИЕ ИЛИ ПРАВИЛЬНАЯ ФОРМУЛИРОВКА ОПРЕДЕЛЕНИЯ
ТЕОРИЯ:

ПРАКТИКА:
Х1=Х+а
0=-1+а
а=1
у1=у+в
-2=-3+в
в= 1
Ответ: а=1; в=1
ПРОВЕРЬ СЕБЯ!

ПРАКТИКА:
0
1
.
.А1
а
Х1=-1+6
Х1 =5
у1=2+3
у1 =5
ПРОВЕРЬ СЕБЯ!
А1(5;5)
5
6
3
5
у
х
А

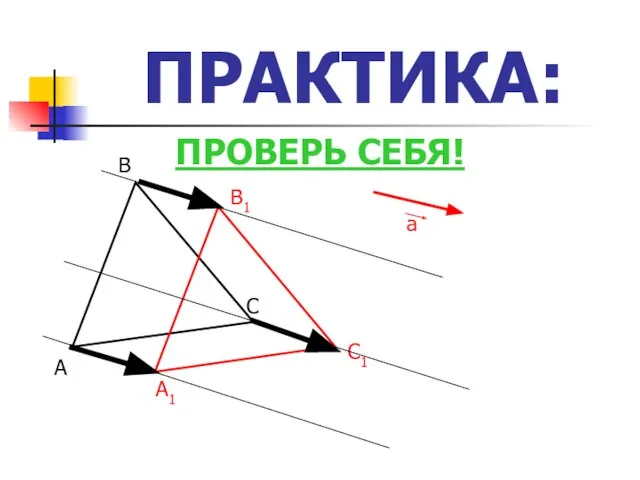
ПРАКТИКА:
А
А1
В
В1
С
С1
ПРОВЕРЬ СЕБЯ!
а

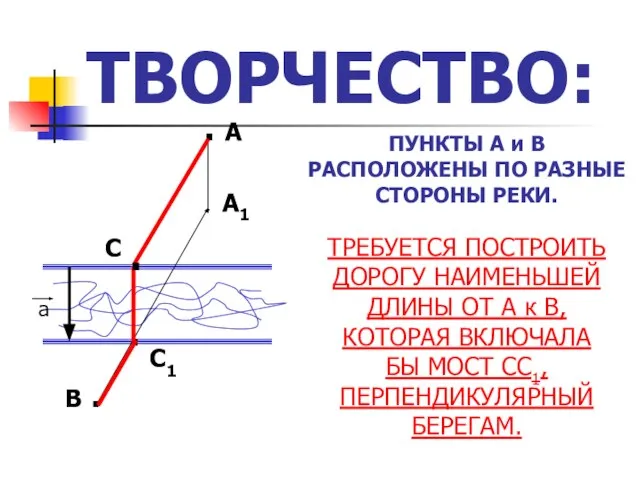
ТВОРЧЕСТВО:
ПУНКТЫ А и В РАСПОЛОЖЕНЫ ПО РАЗНЫЕ СТОРОНЫ РЕКИ.
. А
В .
ТРЕБУЕТСЯ ПОСТРОИТЬ ДОРОГУ НАИМЕНЬШЕЙ ДЛИНЫ ОТ А к В, КОТОРАЯ ВКЛЮЧАЛА БЫ МОСТ СС1, ПЕРПЕНДИКУЛЯРНЫЙ БЕРЕГАМ.
а
А1
.
С1
.
С

ДОМАШНЕЕ ЗАДАНИЕ:
- ВЫПОЛНИТЬ К ЗАДАЧЕ ЧЕРТЕЖ наименьшего пути АСС1В
- ВЫПОЛНИТЬ К ЗАДАЧЕ ЧЕРТЕЖ любого другого пути
- ДОКАЗАТЬ, ЧТО ДЛИНА ЛОМАНОЙ АСС1В - НАИМЕНЬШАЯ