Муниципальное общеобразовательное учреждение гимназия № 12 История математики на линии времени

Цель работы:
Установить соответствие координатной прямая и «линии времени».
Систематизировать события в истории математики на линии времени.
Создать программный продукт
«Книга событий».
Выяснить периоды развития математики.

До нашей эры
Наша эра
Рождество Христово
C1
C2
C3
D
E
Построим координатную прямую, взяв за единичный отрезок – 1 век.
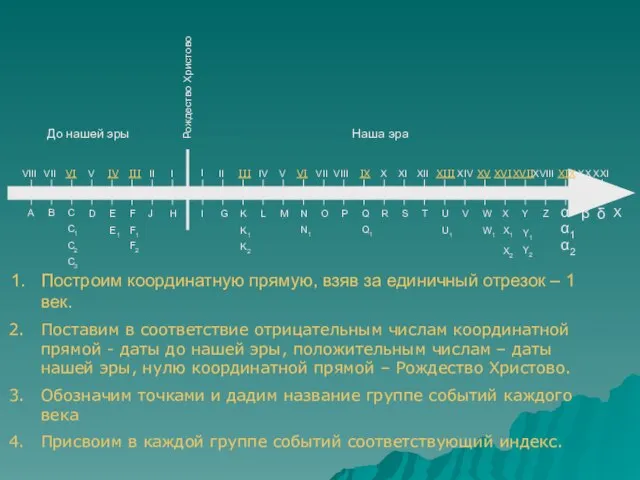
Поставим в соответствие отрицательным числам координатной прямой - даты до нашей эры, положительным числам – даты нашей эры, нулю координатной прямой – Рождество Христово.
Обозначим точками и дадим название группе событий каждого века
Присвоим в каждой группе событий соответствующий индекс.
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII
XIII
XIV
XV
XVI
XVIII
XIX
XX
XXI
I
II
III
IV
V
VI
VII
VIII
X
A
B
F
J
H
I
G
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y1
Y2
Z
α
β
XVII
δ
F1
E1
K1
Q1
U1
W1
α1
С
Y
F2
K2
N1
X1
α2
X2

До нашей эры
Наша эра
Рождество Христово
C1
C2
C3
D
E
Вывод: координатная прямая и «линия времени» находятся во взаимно-однозначном соответствии
Для дальнейшей работы необходимо выбрать интересующий век и прочесть материалы исторического аспекта развития математики
I
II
III
IV
V
VI
VII
VIII
IX
X
XI
XII
XIII
XIV
XV
XVI
XVIII
XIX
XX
XXI
I
II
III
IV
V
VI
VII
VIII
X
A
B
F
J
H
I
G
K
L
M
N
O
P
Q
R
S
T
U
V
W
X
Y1
Y2
Z
α
β
XVII
δ
F1
E1
K1
Q1
U1
W1
α1
С
Y
F2
K2
N1
X1
α2
X2

VI век до нашей эры
Группа С

Фалéс из Милета (ок. 625 до н. э. — ок. 545 до н. э.) — древнегреческий философ; военный инженер лидийских царей; совершал далекие путешествия с познавательными целями. Именем Фалеса названа одна из теорем геометрии. Важнейшей заслугой Фалеса в области математики должно быть считаемо перенесение им из Египта в Грецию первых начал теоретической элементарной геометрии. Эвдем, по свидетельству Прокла, приписывает Фалесу открытие следующих геометрических предложений:
Вертикальные углы равны.
Углы при основании равнобедренного треугольника равны.
Треугольник определяется стороной и прилежащими к ней двумя углами.
Диаметр делит круг на две равные части.
Диоген Лаерций, в основании слов Памфилия, прибавляет к этому списку предложений ещё вписывание в круг прямоугольного треугольника. Чтобы дать полный очерк геометрических знаний Фалеса, необходимо присоединить ещё ряд таких предложений, без которых приобретение первых делается невозможным, а именно предложений о параллельных прямых, о равносторонних, равнобедренных и разносторонних треугольниках, о параллелограммах и пр.

Дошедшие до нас естественнонаучные и философские труды античных ученых и сведения о них показали, что в древней Греции сложились основные типы мировоззрений, действовали различные естественнонаучные школы. В школе Пифагора заметен процесс накопления абстрактных математических фактов и соединения их в теоретические системы. Так из арифметики была выделена в отдельную область теория чисел, т.е. совокупность математических знаний, относящихся к общим свойствам операций с натуральными числами. В это же время стали известными способы суммирования простейших арифметических прогрессий. Рассматривались вопросы делимости чисел, введены арифметическая, геометрическая и гармоническая пропорция.

Пифаго́р Са́мосский ( 570—490 гг. до н. э.) — древнегреческий философ и математик, создатель религиозно-философской школы пифагорейцев.
В современном мире Пифагор считается великим математиком и космологистом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев.»
Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы треугольника равняется сумме квадратов катетов. Такое мнение основывается на сведениях Аполлодора-исчислителя (личность не идентифицирована) и на стихотворных строках (источник стихов не известен):
Современные историки предполагают, что Пифагор не доказывал теорему, но мог передать грекам это знание, известное в Вавилоне за 1000 лет до Пифагора (согласно вавилонским глиняным табличкам с записями математических уравнений). Хотя сомнение в авторстве Пифагора существует, но весомых аргументов, чтобы это оспорить, нет.
К линии времени

IV век до нашей эры
Группа E
К линии времени

III век до нашей эры
Группа F

Евкли́д или Эвклид — древнегреческий математик, живший, согласно Проклу, во время правления Птолемея I, он моложе учеников Платона и старше Архимеда и Эратосфена. По наиболее распространенной версии Евклид работал в Александрии в III веке до н. э.
Главный труд Евклида - Начала (лат. Elementa) - посвящен аксиоматическому построению геометрии и состоит из 13-ти книг, к которым присоединяют две книги о пяти правильных многогранниках, иногда приписываемых Гипсиклу Александрийскому. Собственно геометрия прямых линий, кругов и плоских фигур заключается в первых шести книгах, а в пяти последних книгах изучаются поверхности и тела, в 7-й, 8-й и 9-й книгах рассматриваются свойства чисел, в 10-й рассматриваются в подробности величины несоизмеримые. В сети доступны греческий текст по изданию Гейберга, перевод на английский и русский языки.
Следует подчеркнуть, что до настоящего момента не дошли более ранние произведения, в которых давались бы не рецепты вычислений и построений, но что-либо доказывалось; поздние античные произведения существенно уступают Евклиду. Этот труд оказывал огромное влияние на развитие математики вплоть до Новейшего времени.

Архиме́д (287 до н. э. — 212 до н. э.) — великий древнегреческий математик, механик и инженер из Сиракуз. Сделал множество открытий в геометрии. Заложил основы механики, гидростатики, автор ряда практически важных изобретений.
Архимед был замечательным механиком — и практиком, и теоретиком, но основным делом его жизни была математика. По словам Плутарха, Архимед был просто одержим ею. Он забывал о пище, совершенно не заботился о себе. Его работы относились почти ко всем областям математики того времени: ему принадлежат замечательные исследования по геометрии, арифметике, алгебре. Так, он нашёл все полуправильные многогранники, которые теперь носят его имя, значительно развил учение о конических сечениях, дал геометрический способ решения кубических уравнений, корни которых он находил с помощью пересечения параболы и гиперболы. Архимед провёл и полное исследование этих уравнений, то есть нашёл, при каких условиях они будут иметь действительные положительные различные корни и при каких корни будут совпадать.
К линии времени

III век
Группа K

Первоначально в Китае использовалась десятичная иероглифическая система счисления. Особого знака, нуля при такой системе записи, очевидно, не требуется. Нуль появился только в XII веке и был заимствован из математики Индии. Правила действий, которые использовались в Китае обычные: особенностью является только то, что при делении дробей требуется предварительное приведение их к общему знаменателю.

Диофа́нт Александри́йский (др.-греч. Διόφαντος ὁ Ἀλεξανδρεύς; Diophantus) — древнегреческий математик, живший предположительно в III веке н. э.
Главный труд Диофанта стоит особняком в античной математической библиотеке. Начиная с Евдокса, числовые теории греков строятся на геометрической основе: квадрат числа понимается как площадь квадрата и т. п. Диофант решительно порывает с этой традицией и возвращается к вавилонской алгебре. Первая книга начинается обширным введением, где читатель знакомится с подходом автора. Диофант принимает следующие обозначения: неизвестную он называет «числом» и обозначает буквой ξ, квадрат неизвестной — символом δν и т. д. Предусмотрены специальные значки для степеней неизвестного, включая и отрицательные. Особые символы обозначали знак равенства и отрицательные числа. Знак сложения подразумевался. Рациональные числа трактуются так же, как и целые, что тоже не типично для античных математиков. Сформулированы многие привычные нам правила алгебры: смена знака при переносе в другую часть уравнения, сокращение общих членов и др. Есть даже правило знаков: минус на минус даёт плюс. Всё это формулируется, как и положено в алгебре, в общем виде, без отсылки к геометрическим истолкованиям.
К линии времени

VI век
Группа N
К линии времени

IX век
Группа Q

В вычислительной практике арабоязычных народов равноправно действовали две системы счисления: десятичная абсолютная и 60-ричная. Первая была заимствована из Индии не позднее VII века и быстро получила широкое распространение. Из арифметического трактата Хорезми (IX век) «Об индийских числах», десятичная система стала известна в Европе. В духе математиков древнего Вавилона составлялись и использовались вспомогательные таблицы наподобие таблиц умножения. Для удобства вычислений были разработаны правила перевода из одной системы в другую.
К линии времени

XIII век
Группа U

Боэций Дакийский (родился около 1230-1284) - один из основных представителей «латинского аверроизма», или радикального аристотелизма, независимого философского учения, возникшего в Парижском университете в 60-х годах XIII века.
Многие его сочинения по логике, «модистской» семантике, комментарии к Аристотелю сохранились до нашего времени. Список из тринадцати его работ есть в сводном каталоге авторов-доминиканцев, что отчасти потверждает его принадлежность к ордену.
В 1277 г. он вместе с Сигером Брабантским, был осужден за "преподавание недолжных мнений по вопросам философии и отношения философии к богословию" декретом парижского епископа.
К линии времени

XV век
Группа W

Леона́рдо да Ви́нчи (15 апреля 1452, близ Флоренции — 2 мая 1519, замок Клу, близ Амбуаза, Турень, Франция) — великий итальянский художник и учёный, яркий представитель типа «универсального человека» (homo universale) — идеала итальянского Ренессанса.
Сын флорентийского нотариуса и крестьянки, ученик Вероккио в области живописи, быстро опередивший своего учителя, Леонардо да Винчи жил и работал сначала в купеческой Флоренции, затем при дворах различных князей, всюду предлагая грандиозные планы и нигде не находя настоящего понимания. Усталый и разочарованный, Леонардо да Винчи в январе 1516 принял приглашение короля Франциска I переехать во Францию и здесь прожил последние четыре года своей жизни в замке Клу (в Турени), завершая начатые работы.
Леонардо не имел фамилии в современном смысле; «да Винчи» означает просто «(родом) из городка Винчи». Полное его имя — итал. Leonardo di ser Piero da Vinci, то есть «Леонардо, сын господина Пьеро из Винчи».
К линии времени

XVI век
Группа X

Си́мон Сте́вин (лат. Simon Stevin, 1548 — 1620) — фламандский математик-универсал, инженер.
Подробности о жизни Стевина до нас не дошли. Он начинал как купец из Брюгге, (сейчас это Бельгия), участвовал в голландской революции. Не установлены точные даты его рождения и смерти, неясно даже, в каком городе он умер (то ли Гаага, то ли Лейден). Известно, что он много путешествовал по торговым делам, затем некоторое время был личным советником принца Морица Оранского.
Симон Стевин стал известен прежде всего своей книгой «Десятая» (De Thiende), изданной на фламандском и французском языках в 1585 г. Именно после неё в Европе началось широкое использование десятичных дробей. Десятичные индо-арабские цифры укоренились в Европе намного раньше, с XIII века, а вот дроби использовались либо натуральные, либо шестидесятиричные, либо масштабированные до целых чисел. Например, когда Региомонтан составил первую чисто десятичную таблицу тангенсов (1467), она содержала целые числа, соответствующие радиусу круга 100000 единиц. Правда, Виет, Иммануил Бонфис и некоторые другие математики уже начали использовать десятичные дроби, но правилом это ещё не стало.

Франсуа Виет (или Вьет) (фр. François Viète, seigneur de la Bigotière, 1540—1603) — выдающийся французский математик XVI века, положивший начало алгебре как науке.
Родился в 1540 году в Фонтене-ле-Конт французской провинции Пуату — Шарант. По образованию и основной профессии — юрист, с 19 лет занимался адвокатской практикой в родном городе, по склонности души — математик. Около 1570 г. подготовил «Математический Канон» — труд по тригонометрии, — который издал в Париже в 1579 году.
В 1571 году переехал в Париж и вскоре перешёл на государственную службу, но увлечение его математикой продолжало расти.
Отчасти благодаря браку своей ученицы с принцем де Роганом Виет сделал блестящую карьеру и стал советником сначала короля Генриха III, а после его смерти — Генриха IV. По поручению Генриха IV Виет сумел расшифровать переписку испанских агентов во Франции.
Когда в результате придворных интриг Виет был устранён от дел (1584), он полностью посвятил себя математике. Изучил труды классиков (Кардано, Бомбелли, Стевина и др.). Итогом его размышлений стали несколько трудов, в которых Виет предложил новый язык «общей арифметики» — символический язык алгебры.
К линии времени

XVII век
Группа Y

Рене́ Дека́рт (фр. René Descartes; лат. Renatus Cartesius — Картезий; 31 марта 1596, Лаэ (провинция Турень), ныне Декарт (департамент Эндр и Луара) — 11 февраля 1650, Стокгольм) — французский математик, физик, физиолог и философ, создатель знаменитого метода координат, сторонник аналитического метода в математике, метода радикального сомнения в философии, механицизма в физике, предтеча рефлексологии.

Сэр Исаак Ньютон (англ. Sir Isaac Newton, 25 декабря 1642 — 20 марта 1727 по юлианскому календарю, использовавшемуся в Англии в то время; или 4 января 1643 — 31 марта 1727 по григорианскому календарю) — английский физик, математик, астроном, философ, теолог и алхимик; автор работы «Математические начала натуральной философии» (лат. Philosophiae Naturalis Principia Mathematica) (опубликовано 5 июля 1687), в которой он описал закон всемирного тяготения и так называемые Законы Ньютона, заложившие основы классической механики.
Считается создателем дифференциального и интегрального исчисления одновременно с Г. Лейбницем, и независимо от него.
Хотя во многих открытиях, традиционно приписываемых целиком Ньютону, он имел очень серьёзных предшественников, и доля их вклада далеко не всегда точно и справедливо отражается распространённой традиционной точкой зрения (см. ссылки ниже), тем не менее Ньютону, несомненно, принадлежит во всяком случае крайне существенная по значению, трудности и виртуозности работы доля.
К линии времени

XIX век
Группа α

Никола́й Ива́нович Лобаче́вский (20 ноября (1 декабря) 1792, Нижний Новгород — 12 февраля (24 февраля) 1856, Казань), русский математик, создатель геометрии Лобачевского, мыслитель-материалист, деятель университетского образования и народного просвещения.
Сохранились студенческие записи лекций Лобачевского (от 1817), где им делалась попытка доказать постулат параллельности Евклида, но в рукописи учебника «Геометрия» (1823) он уже отказался от этой попытки. В «Обозрениях преподавания чистой математики» на 1822/23 и 1824/25 Лобачевский указал на «до сих пор непобедимую» трудность проблемы параллелизма и на необходимость принимать в геометрии в качестве исходных понятия, непосредственно приобретаемые из природы.
7 февраля 1826 Лобачевский представил для напечатания в Записках физико-математического отделения сочинение: «Сжатое изложение начал геометрии со строгим доказательством теоремы о параллельных» (на французском языке). Но издание не осуществилось. Рукопись и отзывы не сохранились, однако само сочинение было включено Лобачевским в его труд «О началах геометрии» в журнале «Казанский вестник» (1829—1830), явившийся первой в мировой литературе публикацией по неевклидовой геометрии или Геометрии Лобачевского.
К линии времени