На каких трех «китах» держится информатика?

Алгебра логики

Цели:
Немного об истории логики.
Дать определение логики как науки.
Сформулировать основные формы мышления.
Разобрать какие базовые логические операции существуют?
Привить навыки логически рассуждать.
Записать в тетрадь основные понятия.

1 этап
формальная логика
Основатель – Аристотель
(384 -322гг. до н.э. )
Ввёл основные формулы абстрактного мышления

2 этап
математическая логика
Основатель – немецкий ученый
и философ Лейбниц(1642 -1716), предпринял попытку логических вычислений.

3 этап
Алгебра высказываний
(Булева алгебра)
Основатель – английский математик Джордж Буль(1815 – 1864),ввёл алфавит,
орфографию и грамматику
для математической логики.

В настоящее время самым впечатляющим
у человеческого интеллекта является способность принимать правильные решения в условиях неполной и нечеткой информации.
Построение моделей приближенных размышлений человека и использование их в компьютерных системах представляет сегодня одну из важнейших проблем науки.

Основы нечеткой логики были заложены в конце 60-х лет
в работах всемирно-известного математика, азербайджанского происхождения Лютфи Заде.
Он родился в Баку, Азербайджан
4 февраля l92l года.
«На протяжении всей жизни моя первая любовь - наука и техника» Лютфи Заде

Логика - это наука о формах и способах мышления.
Понятие;
Высказывание;
Умозаключение
Основные формы мышления:

это форма мышления, фиксирую-
щая основные, существенные признаки объекта.
Понятие
Содержание
Объем

Высказывание может быть
истинно или ложно.
Высказывание
это форма мышления,
в которой что-либо утверждается или отрицается о реальных предметах, их свойствах и отношениях между ними.

Посылками умозаключения по правилам формальной логики могут быть только истинные суждения.
Умозаключение
это форма мышления,
с помощью которой из одного или несколько суждений (посылок) может быть получено новое суждение (заключение).

В алгебре высказываний высказывания обозначаются именами логических переменных, которые могут принимать лишь два значения «истинно» и «ложно».
Истинно = 1
Ложно = 0
Алгебра высказываний

Для образования новых высказываний используются базовые логические операции:
инверсия
логическое отрицание
операция не
конъюнкция
дизъюнкция
логическое умножение
операция и
логическое сложение
операция или

Логическое отрицание -операция НЕ инверсия
НЕ
А
А

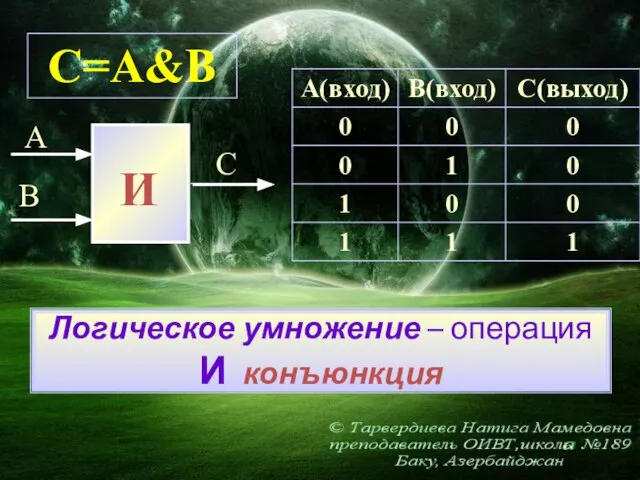
Логическое умножение – операция И конъюнкция
C=A&B

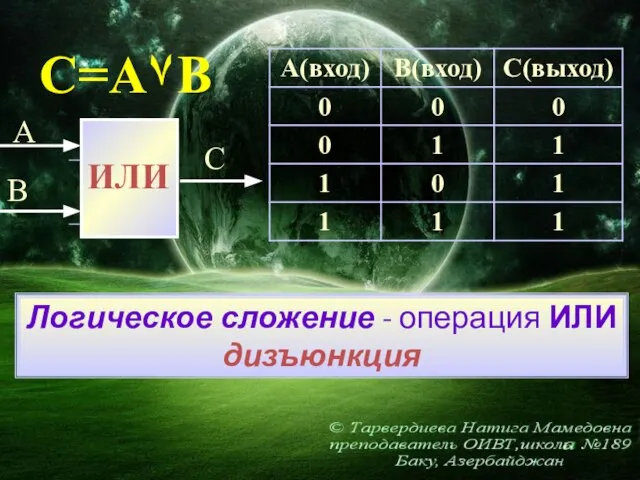
Логическое сложение - операция ИЛИ дизъюнкция
C=A۷B

Каждое составное высказывание можно выразить в виде формулы (логического выражения), в которую входят логические переменные, обозначающие высказывания, и знаки логических операций, обозначающие логические функции.
Логические выражения