Содержание
- 2. УПИ – единственное уравнение классической матфизики сформулированное российской научной школой Уравнение переноса излучения
- 3. В теории переноса возникает возможность усиления света Теория переноса и лазеры Outside of thermodynamic equilibrium, the
- 4. Теория переноса – важное направление исследований на ЭТФ Теория переноса в МЭИ
- 5. Заслуга Савенкова В.И., Мельникова Г.А., что они определили задачи светового поля, как краевые задачи УПИ Теория
- 6. Центральной проблемой теории оставалось сильно анизотропное рассеяние Состояние теории переноса в мире Амбарцумян В.А. К задаче
- 7. Астрофизика, частицы, оптика атмосфера, оптика океана Особенности развития в нашей стране Метод Монте-Карло в атмосферной оптике
- 8. МСГ сводит систему дифференциальных уравнений к одному уравнению в частных производных Этапы развития теории переноса на
- 9. МСГ точно описывает анизотропную часть решения УПИ, открывая путь к описанию сильно анизотропного рассеяния Малоугловая модификация
- 10. Выделение анизотропии позволяет заменить интеграл рассеяния конечной суммой – дискретизация УПИ Устранение анизотропии в решении Eddington,
- 11. В окрестности особенности углового распределения яркости ее спектр убывает медленно и монотонно Малоугловая модификация метода сферических
- 12. В отличие от Goudsmit-Sounderson, где система уравнений разваливается на независимые, здесь уравнения зацепляются Решение полученного уравнения
- 13. Дискретизация приводит к матричному решению, сложность вычислений определяется размером матриц Регулярная часть решение
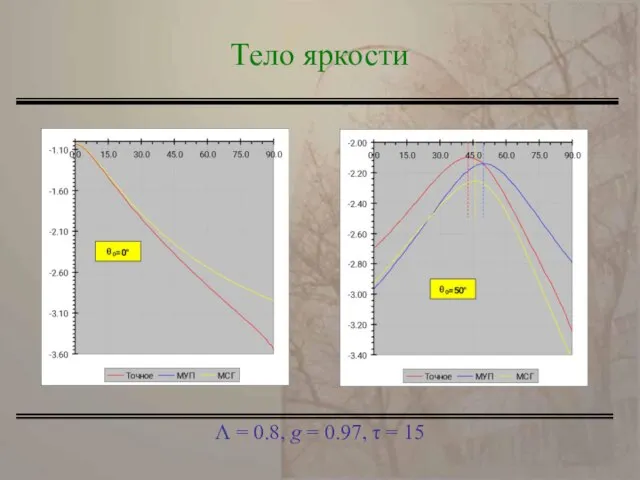
- 14. Λ = 0.8, g = 0.97, τ = 15 Тело яркости
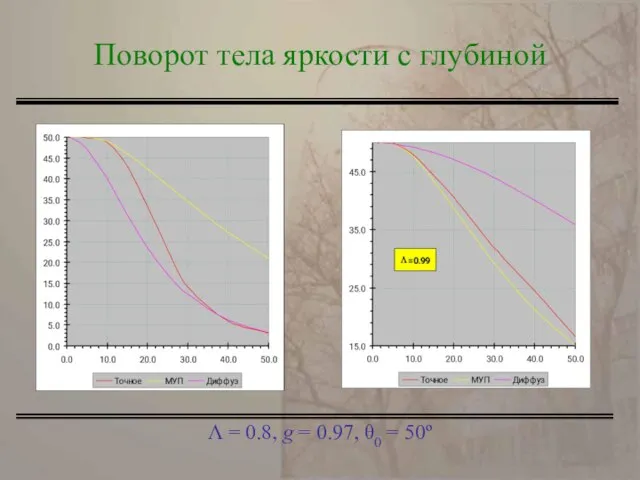
- 15. Λ = 0.8, g = 0.97, θ0 = 50º Поворот тела яркости с глубиной
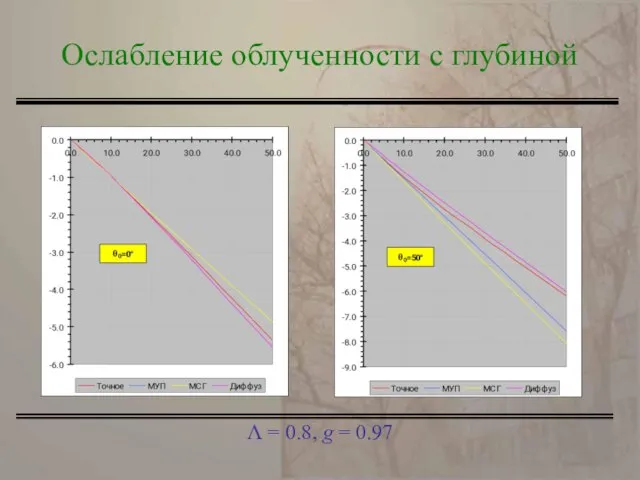
- 16. Λ = 0.8, g = 0.97 Ослабление облученности с глубиной
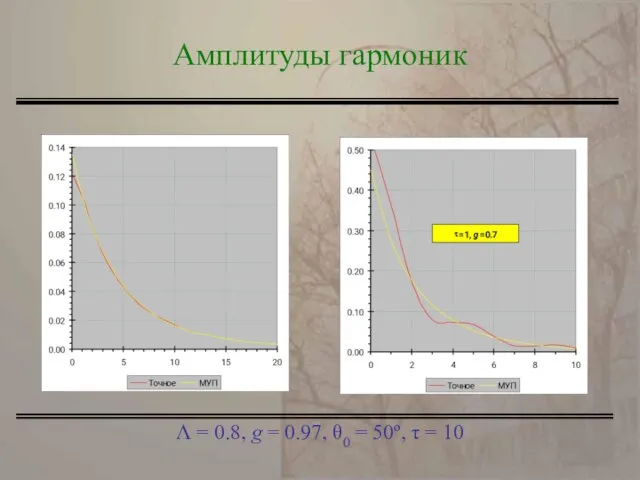
- 17. Λ = 0.8, g = 0.97, θ0 = 50º, τ = 10 Амплитуды гармоник
- 18. Абсолютно идентичная форма решения, но матрицы 4N × 4N Векторное обобщение
- 19. Абсолютно идентичная форма решения, но матрицы 4N × 4N Векторное обобщение Взаимосвязь граничных условий Граница раздела
- 21. Скачать презентацию














 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм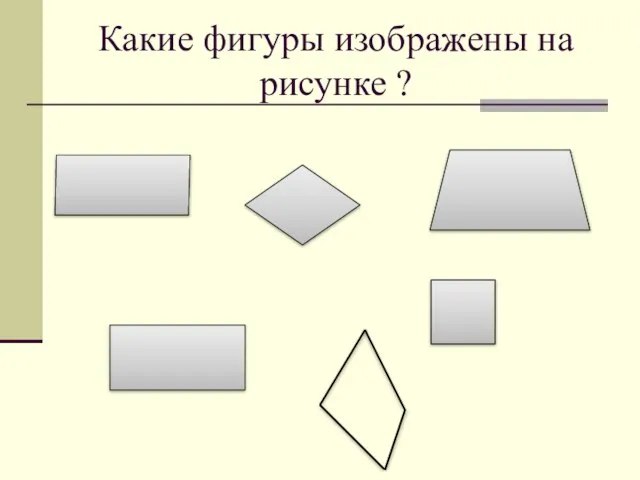 Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом