Содержание
- 2. Актуальность Большинство современных вычислительных задач требует для своего решения ресурсов, превосходящих возможности однопроцессорных компьютеров. Возникают новые
- 3. Основные задачи диссертационной работы Разработка метода введения обобщённых координат для решеток клеточных автоматов. Разработка на основе
- 4. Положения, выносимые на защиту и их научная новизна
- 5. Практическая полезность
- 6. Клеточный автомат Клеточный автомат A представляет собой четверку объектов {G, Z, N, f}, где: G –
- 7. Обобщённые координаты Обобщённая координата – неотрицательное целое число, однозначно указывающее на клетку решетки клеточного автомата произвольной
- 8. Обобщённые координаты для треугольной решетки, базирующиеся на спиральных обобщённых координатах для шестиугольной решетки Спиральные обобщённые координаты
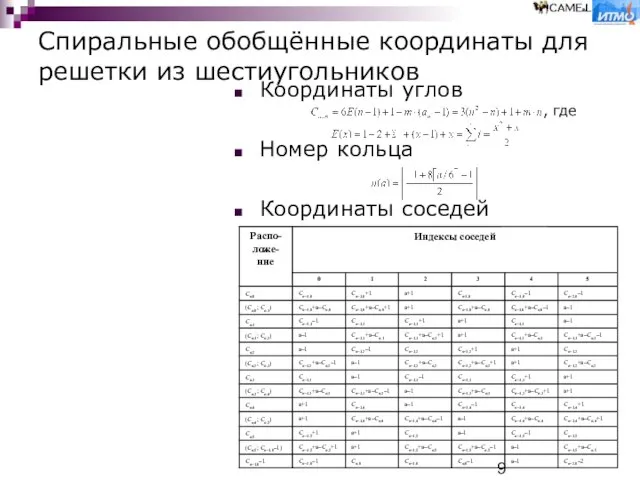
- 9. Координаты углов Номер кольца Координаты соседей , где Спиральные обобщённые координаты для решетки из шестиугольников
- 10. Сравнение эффективности различных способов введения обобщённых координат Приняв за единицу измерения производительности средние показатели самого медленного
- 11. Преимущества и недостатки обобщённых координат Преимущества Обобщённые координаты обеспечивают универсальность организации данных, позволяя хранить состояния различных
- 12. Компонентная модель декомпозиции клеточных автоматов Каждый клеточный автомат целесообразно представлять набором компонентов следующих четырех типов: Решетка
- 13. Требования к инструментальным средствам (1) Предоставлять пользователям дружественный, удобный, современный интерфейс с богатым набором возможностей для
- 14. Требования к инструментальным средствам (2) Предоставлять пользователям дружественный, удобный, современный интерфейс с богатым набором возможностей для
- 15. Структурная схема инструментального средства CAME&L = среда выполнения + библиотека CADLib + стандартные компоненты CAME&L –
- 16. Методика организации и проведения вычислительных экспериментов Запуск среды выполнения. При проведении эксперимента в вычислительном кластере, необходимо
- 17. Применение методики на примере игры "Жизнь" Выбор решетки. Для моделирования требуется двумерная квадратная решетка. Компонент, "Square
- 18. Уравнение теплопроводности Непрерывный вариант: Дискретный вариант (при a, dx и dy = 1):
- 19. Существует 256 функций переходов для простейших одномерных двоичных клеточных автоматов. Рассмотрены и пронумерованы 256 структур, порождаемых
- 20. Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (2) Впервые проведена полная классификация этих структур
- 21. Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (3) Число классов при разных вариантах классификации
- 22. Внедрение Научные исследования В СПбГУ ИТМО при исследованиях по грантам Министерства образования и науки РФ, а
- 23. Использование инструментального средства для организации вычислительных экспериментов на FPGA-системах Разработанный комплекс средств позволяет на основе имеющегося
- 24. Заключение В диссертации получены следующие результаты: Введено понятие "обобщенные координаты" для решеток клеточных автоматов. Разработан метод
- 25. Публикации Наумов Л. Как увеличить скорость "Жизни", или Эффективная организация данных для повышения скорости поиска клеток
- 27. Скачать презентацию
Слайд 2Актуальность
Большинство современных вычислительных задач требует для своего решения ресурсов, превосходящих возможности однопроцессорных
Актуальность
Большинство современных вычислительных задач требует для своего решения ресурсов, превосходящих возможности однопроцессорных

Возникают новые и задачи, которые нуждаются в параллельной или распределенной архитектуре вычислительной системы для своего решения.
Так как в настоящее время при создании сложных программно-аппаратных комплексов значительная доля затрат идёт на разработку программного обеспечения и эта доля неуклонно увеличивается, задача создания инструментального средства для автоматизации проектирования программного обеспечения систем с параллельной и распределенной вычислительными архитектурами становится актуальной.
Наглядной, общей и широко используемой моделью параллельных вычислений, которая может быть применена при создании такого средства, являются клеточные автоматы – дискретные динамические системы, поведение которых может быть полностью описано в терминах локальных зависимостей.
Слайд 3Основные задачи диссертационной работы
Разработка метода введения обобщённых координат для решеток клеточных автоматов.
Разработка
Основные задачи диссертационной работы
Разработка метода введения обобщённых координат для решеток клеточных автоматов.
Разработка

Демонстрация применения инструментального средства для автоматизации проектирования программного обеспечения ряда вычислительных экспериментов с использованием клеточных автоматов на различных вычислительных архитектурах.
Классификация всех структур, которые порождаются одномерными клеточными автоматами из точечного зародыша с целью анализа простейших клеточных автоматов, демонстрирующих сложное поведение (в том числе, самовоспроизведение).
Слайд 4Положения, выносимые на защиту и их научная новизна
Положения, выносимые на защиту и их научная новизна

Слайд 5Практическая полезность
Практическая полезность

Слайд 6Клеточный автомат
Клеточный автомат A представляет собой четверку объектов {G, Z, N, f},
Клеточный автомат
Клеточный автомат A представляет собой четверку объектов {G, Z, N, f},

G – дискретное метрическое пространство, решетка автомата;
Z – конечное множество возможных состояний клетки. Таким образом, состояние всей решетки является элементом множества Z|G|;
N – конечное множество, определяющее окрестность клетки, то есть те |N| клеток, которые влияют на новое состояние данной. Элементы этого множества будем называть "соседями" клетки;
f – функция переходов или правила автомата. Вычислимая функция, действующая Z×Z|N| → Z для автоматов с клетками с памятью и Z|N| → Z для автоматов с клетками без памяти.
Клеточные автоматы в общем случае характеризуются следующими фундаментальными свойствами:
Решетка однородна – никакие две области не могут быть отличены друг от друга по ландшафту. Это обеспечивается семантикой пространства G, а также единственностью определения окрестности N, множества значений Z и функции переходов f.
Взаимодействия локальны. Состояния только клеток окрестности влияют на состояние данной клетки, что обеспечивается семантикой функции f.
Обновление значений состояний всех клеток решетки происходит одновременно после вычисления нового состояния каждой из них (такие автоматы называются "синхронными").
Слайд 7Обобщённые координаты
Обобщённая координата – неотрицательное целое число, однозначно указывающее на клетку решетки
Обобщённые координаты
Обобщённая координата – неотрицательное целое число, однозначно указывающее на клетку решетки

Метод введения обобщённых координат обеспечит единообразие представления данных для различных решеток.
Он заключается в нумерации клеток неотрицательными целыми числами.
Необходимо обеспечить нахождение непосредственных соседей данной клетки.
Без перехода к декартовым координатам.
Это позволит работать с более сложными окрестностями (искать соседей рекурсивно).
Слайд 8Обобщённые координаты для треугольной решетки, базирующиеся на спиральных обобщённых координатах для шестиугольной
Обобщённые координаты для треугольной решетки, базирующиеся на спиральных обобщённых координатах для шестиугольной

Спиральные обобщённые координаты для шестиугольной решетки
Различные способы введения обобщённых координат
Спиральные обобщённые координаты для квадратной решетки
Спиральные обобщённые координаты для треугольной решетки
Слайд 9Координаты углов
Номер кольца
Координаты соседей
, где
Спиральные обобщённые координаты для решетки из шестиугольников
Координаты углов
Номер кольца
Координаты соседей
, где
Спиральные обобщённые координаты для решетки из шестиугольников
Слайд 10Сравнение эффективности различных способов введения обобщённых координат
Приняв за единицу измерения производительности средние
Сравнение эффективности различных способов введения обобщённых координат
Приняв за единицу измерения производительности средние
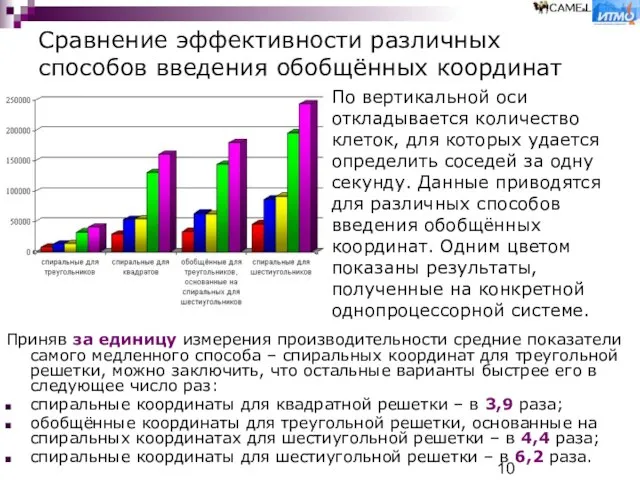
спиральные координаты для квадратной решетки – в 3,9 раза;
обобщённые координаты для треугольной решетки, основанные на спиральных координатах для шестиугольной решетки – в 4,4 раза;
спиральные координаты для шестиугольной решетки – в 6,2 раза.
По вертикальной оси откладывается количество клеток, для которых удается определить соседей за одну секунду. Данные приводятся для различных способов введения обобщённых координат. Одним цветом показаны результаты, полученные на конкретной однопроцессорной системе.
Слайд 11Преимущества и недостатки обобщённых координат
Преимущества
Обобщённые координаты обеспечивают универсальность организации данных, позволяя хранить
Преимущества и недостатки обобщённых координат
Преимущества
Обобщённые координаты обеспечивают универсальность организации данных, позволяя хранить

Существенно более удобным становится изменение размеров решетки.
Одномерную структуру можно рассматривать, как последовательность данных, то есть её удобно сериализовывать и сохранять.
Обобщённые координаты – это идея, которая может быть адаптирована под конкретную задачу с учетом, например, внутренней симметрии моделируемой системы и т.п.
Отсутствие существенной зависимости от положения нуля позволяет перемещать его в соответствии с потребностями задачи.
Недостатки
Скорость разрешения отношения соседства ниже, чем для декартовых координат.
Создание математического аппарата для новых типов решёток и способов введения обобщённых координат является трудоёмким процессом.
Слайд 12Компонентная модель декомпозиции клеточных автоматов
Каждый клеточный автомат целесообразно представлять набором компонентов следующих
Компонентная модель декомпозиции клеточных автоматов
Каждый клеточный автомат целесообразно представлять набором компонентов следующих

Решетка (grid) – осуществляет визуализацию автомата и навигацию;
Метрика (metrics) – сопоставляет клеткам координаты, вводит отношение соседства и функции вычисления расстояний между клетками.
Выделение этого типа компонентов позволит использовать обобщённые координаты и переходить от одних координат к только сменой компонента.
Хранилище данных (datum) – обеспечивает хранение, обмен и преобразования состояний клеток, а также некоторые аспекты визуализации;
Правила (rules) – описывает итерацию, задаёт не только функцию переходов, но и метод разделения задачи на подзадачи, оптимизацию вычислений и т.п.
При реализации целесообразно ввести дополнительный тип компонента:
Анализатор (analyzer) – позволяет наблюдать динамику изменения ключевых параметров эксперимента, строить графики, файлы отчетов и т.п.
Необходимо отметить, что речь идет не о четырех составляющих из определения клеточного автомата ({G, Z, N, f}). В данном случае декомпозицию логичнее вести по другим принципам и руководствоваться вопросам реализации автомата и проектирования вычислительного эксперимента.
Модель компонентной декомпозиции клеточных автоматов позволяет "собирать" автоматы с различной функциональностью, посредством незначительных изменений переходить от одной задачи к другой, пробовать решать одну и ту же задачу на разных решетках, с различными метриками и т.д.
Кроме того, она предоставляет возможность распределять разработку программного обеспечения эксперимента между различными исполнителями.
Слайд 13Требования к инструментальным средствам (1)
Предоставлять пользователям дружественный, удобный, современный интерфейс с богатым
Требования к инструментальным средствам (1)
Предоставлять пользователям дружественный, удобный, современный интерфейс с богатым
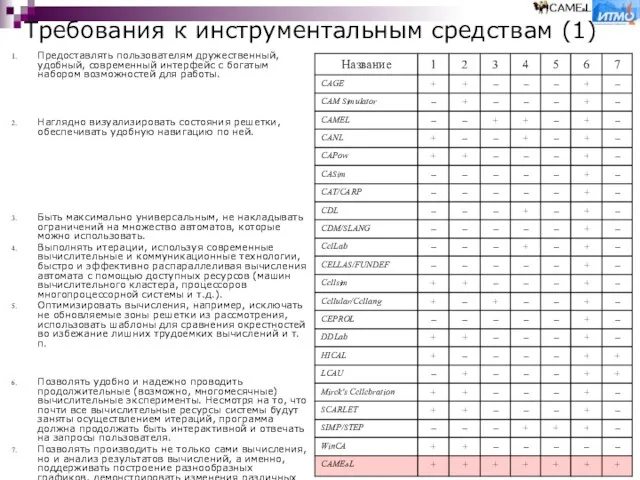
Наглядно визуализировать состояния решетки, обеспечивать удобную навигацию по ней.
Быть максимально универсальным, не накладывать ограничений на множество автоматов, которые можно использовать.
Выполнять итерации, используя современные вычислительные и коммуникационные технологии, быстро и эффективно распараллеливая вычисления автомата с помощью доступных ресурсов (машин вычислительного кластера, процессоров многопроцессорной системы и т.д.).
Оптимизировать вычисления, например, исключать не обновляемые зоны решетки из рассмотрения, использовать шаблоны для сравнения окрестностей во избежание лишних трудоемких вычислений и т.п.
Позволять удобно и надежно проводить продолжительные (возможно, многомесячные) вычислительные эксперименты. Несмотря на то, что почти все вычислительные ресурсы системы будут заняты осуществлением итераций, программа должна продолжать быть интерактивной и отвечать на запросы пользователя.
Позволять производить не только сами вычисления, но и анализ результатов вычислений, а именно, поддерживать построение разнообразных графиков, демонстрировать изменения различных параметров моделируемой системы и т.п.
Слайд 14Требования к инструментальным средствам (2)
Предоставлять пользователям дружественный, удобный, современный интерфейс с богатым
Требования к инструментальным средствам (2)
Предоставлять пользователям дружественный, удобный, современный интерфейс с богатым

Наглядно визуализировать состояния решетки, обеспечивать удобную навигацию по ней.
Быть максимально универсальным, не накладывать ограничений на множество автоматов, которые можно использовать.
Выполнять итерации, используя современные вычислительные и коммуникационные технологии, быстро и эффективно распараллеливая вычисления автомата с помощью доступных ресурсов (машин вычислительного кластера, процессоров многопроцессорной системы и т.д.).
Оптимизировать вычисления, например, исключать не обновляемые зоны решетки из рассмотрения, использовать шаблоны для сравнения окрестностей во избежание лишних трудоемких вычислений и т.п.
Позволять удобно и надежно проводить продолжительные (возможно, многомесячные) вычислительные эксперименты. Несмотря на то, что почти все вычислительные ресурсы системы будут заняты осуществлением итераций, программа должна продолжать быть интерактивной и отвечать на запросы пользователя.
Позволять производить не только сами вычисления, но и анализ результатов вычислений, а именно, поддерживать построение разнообразных графиков, демонстрировать изменения различных параметров моделируемой системы и т.п.
Интерфейс предложенного инструментального средства чрезвычайно богат и поддерживает множество типичных функций, присутствия которых пользователь в праве ожидать от современного программного обеспечения.
За визуализацию состояния решетки и удобную навигацию по ней отвечает отдельный класс компонентов. Пользователю предоставляется стандартный набор средств для этих целей, кроме того, он может быть расширен с помощью новых компонентов, обладающих конкретными специфическими свойствами, необходимыми для решения задач.
Инструментальное средство позволяет моделировать класс систем даже более широкий, чем класс "клеточные автоматы".
Средство позволяет организовывать вычисления, как на отдельном персональном компьютере, так и на многопроцессорной системе и в вычислительном кластере.
Средства для оптимизации вычислений включены в стандартный пакет программного обеспечения и могут быть применены при решении пользовательских задач. Этот набор также может быть легко расширен пользователями при необходимости.
Проект позволяет удобно и надежно проводить продолжительные вычислительные эксперименты, сохраняя при этом интерактивность и предоставляя возможности управления его течением.
Инструментальное средство использует специальные компоненты-анализаторы для наблюдений и изучения динамики ключевых параметров эксперимента, построения графиков, файлов-отчетов и прочих задач такого рода.
Слайд 15Структурная схема инструментального средства
CAME&L = среда выполнения + библиотека CADLib + стандартные
Структурная схема инструментального средства
CAME&L = среда выполнения + библиотека CADLib + стандартные
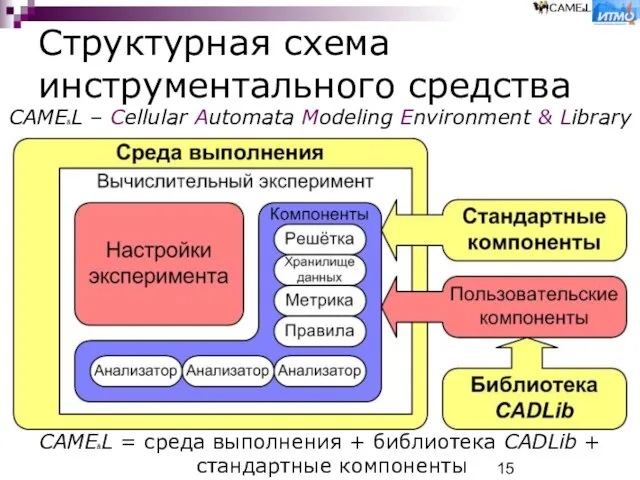
CAME&L – Cellular Automata Modeling Environment & Library
Слайд 16Методика организации и проведения вычислительных экспериментов
Запуск среды выполнения.
При проведении эксперимента в вычислительном
Методика организации и проведения вычислительных экспериментов
Запуск среды выполнения.
При проведении эксперимента в вычислительном

Выбор решетки. Если подходящая решетка есть в наборе стандартных компонентов, то выбрать ее. Иначе – создать новый компонент.
Выбор метрики. Если подходящая метрика есть в наборе стандартных компонентов, то выбрать ее. Иначе – создать новый компонент.
Выбор хранилища данных. Если подходящее хранилище данных есть в наборе стандартных компонентов, то выбрать его. Иначе – создать новый компонент.
Выбор правил. Если подходящие правила есть в наборе стандартных компонентов, то выбрать их. Иначе – создать новый компонент.
Настройка компонентов. Установить требуемые значения параметров.
Запуск эксперимента путем выбора соответствующей команды в среде.
Создание и выбор нового компонента
Разработка компонента. С помощью привычного средства разработки (например, Microsoft Visual C++ 6) создать библиотеку, содержащую класс требуемого компонента, являющийся наследником класса базового класса из библиотеки CADLib.
Компиляция компонента в DLL-библиотеку.
Установка компонента в инструментальном средстве. Для установки, удаления и изучения компонентов в среде выполнения имеется инструмент "Components Manager". Им и необходимо воспользоваться.
Выбор компонента.
Слайд 17Применение методики на примере игры "Жизнь"
Выбор решетки. Для моделирования требуется двумерная квадратная
Применение методики на примере игры "Жизнь"
Выбор решетки. Для моделирования требуется двумерная квадратная

Выбор метрики. Используем декартовы координаты. Компонент "Cartesians", реализующий функциональность декартовой метрики, существует в наборе стандартных.
Выбор хранилища данных. Компонент "Booleans for Cartesians", реализующий функциональность хранилища булевых данных для декартовой метрики, имеется в наборе стандартных.
Выбор правил. Предположим, что компонент, реализующий правила игры "Жизнь" не входит в набор стандартных компонентов. Создадим новый компонент.
Настройка компонентов. Необходимо изменить значение параметра "Double" хранилища данных "Booleans for Cartesians" на "true", выбрав тем самым синхронный клеточный автомат.
Запуск эксперимента.
Создание и выбор нового компонента
Разработка компонента. Создадим класс наследник класса CAUniRules. Переопределим его функцию SubCompute следующим образом:
DATUM(CACrtsBool2DDatum);
CACell c;
CACell neig[12];
int alive=0;
for(CACell i=z.a1; i<=z.b1; i++)
for(CACell j=z.a2; j<=z.b2; j++) {
alive=0;
c=GET_METRICS->ToCell(i,j,0);
GET_METRICS->GetNeighbours(c,neig);
for (unsigned int k=0;
k
k++) if (datum->Get(neig[k]))alive++;
if (datum->Get(c))
datum->Set(c,alive==2||alive==3);
else
datum->Set(c,alive==3);
}
return true;
Компиляция компонента в DLL-библиотеку.
Установка компонента в инструментальном средстве.
Выбор компонента.
Слайд 18Уравнение теплопроводности
Непрерывный вариант:
Дискретный вариант (при a, dx и dy = 1):
Уравнение теплопроводности
Непрерывный вариант:
Дискретный вариант (при a, dx и dy = 1):

Слайд 19Существует 256 функций переходов для простейших одномерных двоичных клеточных автоматов.
Рассмотрены и пронумерованы
Существует 256 функций переходов для простейших одномерных двоичных клеточных автоматов.
Рассмотрены и пронумерованы
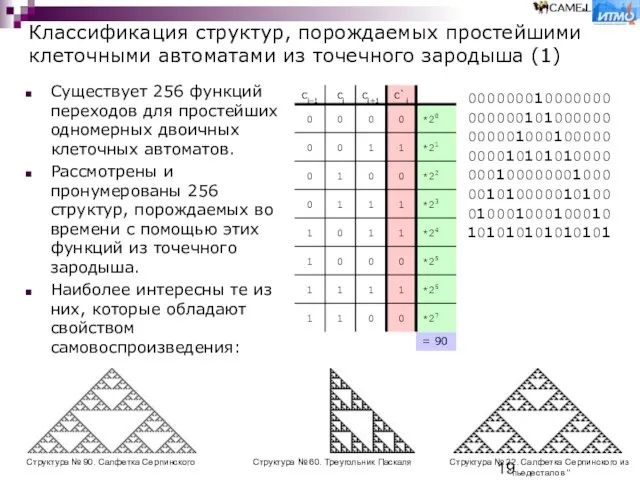
Наиболее интересны те из них, которые обладают свойством самовоспроизведения:
Структура № 90. Салфетка Серпинского
Структура № 22. Салфетка Серпинского из "пьедесталов "
Структура № 60. Треугольник Паскаля
000000010000000
000000101000000
000001000100000
000010101010000
000100000001000
001010000010100
010001000100010
101010101010101
Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (1)
Слайд 20Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (2)
Впервые проведена полная
Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (2)
Впервые проведена полная
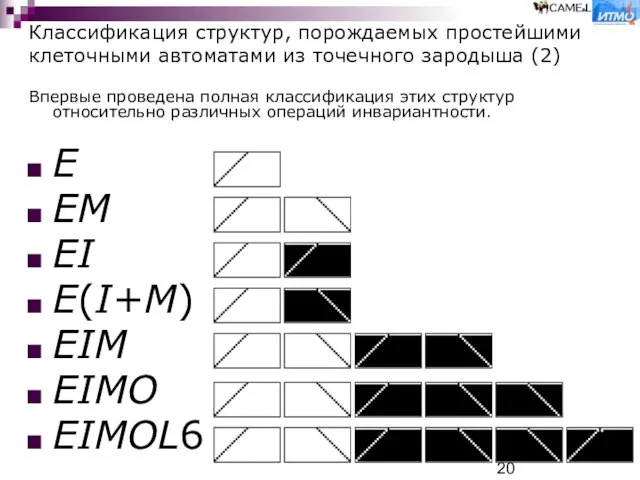
E
EM
EI
E(I+M)
EIM
EIMO
EIMOL6
Слайд 21Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (3)
Число классов при
Классификация структур, порождаемых простейшими клеточными автоматами из точечного зародыша (3)
Число классов при
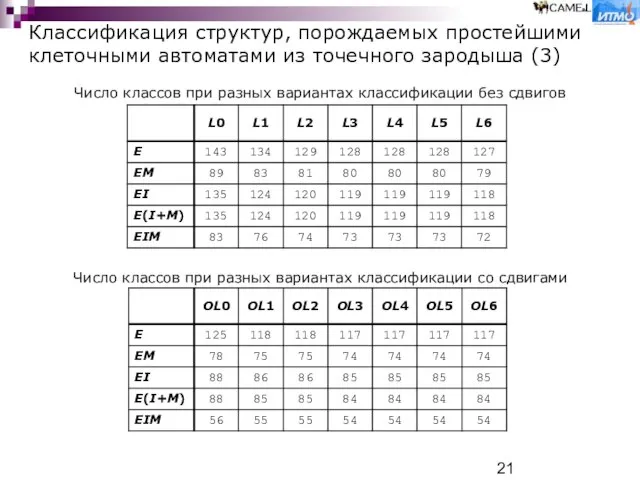
Число классов при разных вариантах классификации со сдвигами
Слайд 22Внедрение
Научные исследования
В СПбГУ ИТМО при исследованиях по грантам Министерства образования и науки
Внедрение
Научные исследования
В СПбГУ ИТМО при исследованиях по грантам Министерства образования и науки
В Университете Амстердама для организации вычислительных экспериментов на FPGA-системах и многих других задач.
Политехническом университете Бухареста при создании инструментального средства для обработки изображений.
Обучение
В СПбГУ ИТМО на кафедре "Компьютерные технологии":
при чтении лекций по курсу "Теория автоматов в программировании";
в курсовых работах студентов по курсу "Теория автоматов в программировании".
В СПбГУ на кафедре "Вычислительная физика":
при чтении лекций по курсу "Современные технологии программирования для научных работников";
для демонстрации решения уравнений вычислительной физики посредством клеточных автоматов.
В Университете Амстердама:
при чтении лекций по курсу "Моделирование поведения сложных систем";
написании дипломных проектов.
Слайд 23Использование инструментального средства для организации вычислительных экспериментов на FPGA-системах
Разработанный комплекс средств позволяет
Использование инструментального средства для организации вычислительных экспериментов на FPGA-системах
Разработанный комплекс средств позволяет
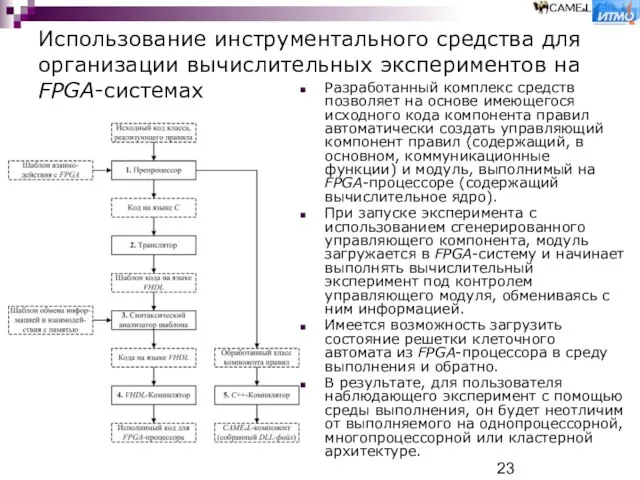
При запуске эксперимента с использованием сгенерированного управляющего компонента, модуль загружается в FPGA-систему и начинает выполнять вычислительный эксперимент под контролем управляющего модуля, обмениваясь с ним информацией.
Имеется возможность загрузить состояние решетки клеточного автомата из FPGA-процессора в среду выполнения и обратно.
В результате, для пользователя наблюдающего эксперимент с помощью среды выполнения, он будет неотличим от выполняемого на однопроцессорной, многопроцессорной или кластерной архитектуре.
Слайд 24Заключение
В диссертации получены следующие результаты:
Введено понятие "обобщенные координаты" для решеток клеточных автоматов.
Заключение
В диссертации получены следующие результаты:
Введено понятие "обобщенные координаты" для решеток клеточных автоматов.

На основе метода введения обобщенных координат и компонентной модели декомпозиции разработано инструментальное средство автоматизации проектирования программного обеспечения вычислительных экспериментов с использованием клеточных автоматов CAME&L.
Метод и инструментальное средство CAME&L апробированы при автоматизации проектирования программного обеспечения ряда вычислительных экспериментов с использованием клеточных автоматов на однопроцессорных, многопроцессорных, кластерных и FPGA вычислительных системах. Ранее было невозможно выполнить это с помощью одного и того же инструментального средства.
Проведена классификация всех возможных структур, порождаемых одномерными клеточными автоматами из точечного зародыша. Построено множество разнообразных классов эквивалентности. Показано, что автоматы с клетками с памятью и автоматы с клетками без памяти могут демонстрировать одинаковое поведение. Таким образом, выполнен анализ простейших клеточных автоматов, порождающих сложное поведение (в том числе, самовоспроизведение).
Результаты были внедрены в учебном процессе и при проведении научных исследований в ряде университетов.
Слайд 25Публикации
Наумов Л. Как увеличить скорость "Жизни", или Эффективная организация данных для повышения
Публикации
Наумов Л. Как увеличить скорость "Жизни", или Эффективная организация данных для повышения

Naumov L. Generalized Coordinates for Cellular Automata Grids / Computational Science – ICCS 2003. Part 2. Springer-Verlag. 2003, c. 869–878.
Наумов Л., Шалыто А. Клеточные автоматы. Реализация и эксперименты // Мир ПК. 2003. № 8, c. 71–78.
Наумов Л. CAME&L – среда моделирования и библиотека разработчика клеточных автоматов / Труды XI Всероссийской научно-методической конференции Телематика’2004. Том 1. СПб.: СПбГУ ИТМО. 2004, c. 184–186.
Наумов Л. CTP (Commands Transfer Protocol) – Сетевой протокол для высокопроизводительных вычислений / Труды XI Всероссийской научно-методической конференции Телематика’2004. Том 1. СПб.: СПбГУ ИТМО. 2004, c. 188–189.
Наумов Л., Шалыто А. "Цветные" клеточные автоматы // Мир ПК. 2004. № 5, c. 64–71.
Naumov L. CAME&L – Cellular Automata Modeling Environment & Library / Cellular Automata. Sixth International Conference on Cellular Automata for Research and Industry, ACRI-2004. Springer–Verlag. 2004, c. 735–744.
Наумов Л. CTP (Commands Transfer Protocol) v. 1.2 – Новая версия сетевого протокола для высокопроизводительных вычислений / Труды XII Всероссийской научно-методической конференции Телематика’2005. Том 1. СПб.: СПбГУ ИТМО. 2005, с. 92–93.
Наумов Л. Преимущества использования обобщённых координат для многомерных решёток клеточных автоматов / Труды XII Всероссийской научно-методической конференции Телематика’2005. Том 1. СПб.: СПбГУ ИТМО. 2005. с. 93–95.
Наумов Л. CAME&L – средство для осуществления параллельных и распределенных вычисления на основе клеточных автоматов / Технологии распределенных вычислений. 2005, с. 284–286.
Наумов Л. Решение задач с помощью клеточных автоматов посредством программного обеспечения CAMEL (Части I и II) // Информационно-управляющие системы. 2005. № 5, c. 22–30; № 6, c. 30–38.
Наумов Л., Шалыто А. Классификация структур, порождаемых одномерными двоичными клеточными автоматами из точечного зародыша // Известия РАН. Теория и системы управления. 2005. № 5, с. 137–145. Журнал из списка ВАК. Naumov L., Shalyto A. Classification of Structures Generated by One-Dimensional Binary Cellular Automata from a Point Embryo // Journal of Computer and Systems Sciences International. Vol. 44. 2005. № 5, pp. 800–807.
Наумов Л. Сравнение специализированных сетевых протоколов CTP (Commands Transfer Protocol) и IL (Internet Link) / Труды XIII Всероссийской научно-методической конференции Телематика’2006. Том 1. СПб.: СПбГУ ИТМО. 2006, с. 266–267.
Наумов Л. Обзор программного обеспечения для решения задач с использованием клеточных автоматов // Телекоммуникации и информатизация образования. 2006. № 2, c. 114–125.
Все статьи и инструментальное средство – опубликованы на сайте http://camellab.spb.ru.
 За пределами стереотипов использования СУЭ АСФК.
За пределами стереотипов использования СУЭ АСФК. Спутниковая фотосъемка
Спутниковая фотосъемка Собор Воскресения Христова на Крови
Собор Воскресения Христова на Крови Феварин в терапии алкогольной зависимости
Феварин в терапии алкогольной зависимости Разработка мер по защите информации в АСУ АСУ – навигация Алтайский край
Разработка мер по защите информации в АСУ АСУ – навигация Алтайский край 6 класс
6 класс Правила перевозки пассажиров на транспортных средствах
Правила перевозки пассажиров на транспортных средствах Экскурсоведение
Экскурсоведение Решение текстовых задач
Решение текстовых задач Научно-исследовательская работа студентов (НИРС)
Научно-исследовательская работа студентов (НИРС) Виды транспорта
Виды транспорта Родительское собрание на тему: «Что такое пассивное курение?»
Родительское собрание на тему: «Что такое пассивное курение?» Тема лекции:«Прикладная информатика в Интернет»
Тема лекции:«Прикладная информатика в Интернет» ОТЛИЧИЯ СОВРЕМЕННОГО УРОКА
ОТЛИЧИЯ СОВРЕМЕННОГО УРОКА Составление сетчатых орнаментов на основе законов симметрии
Составление сетчатых орнаментов на основе законов симметрии Жизнь без сигарет
Жизнь без сигарет Презентация 07.10.2017
Презентация 07.10.2017 Проблемы и задачи. Методы поиска и выбор темы проекта. Занятие №4
Проблемы и задачи. Методы поиска и выбор темы проекта. Занятие №4 Презентация на тему Гендерное воспитание в подготовительной группе
Презентация на тему Гендерное воспитание в подготовительной группе  Добро пожаловать на урок математики!
Добро пожаловать на урок математики! PDCA Action Cards
PDCA Action Cards Проект урока подготовила: учитель I категории: Харькова И.В.
Проект урока подготовила: учитель I категории: Харькова И.В. Кабатлау дәресе. 4 класс
Кабатлау дәресе. 4 класс Презентация на тему Песня… про купца Калашникова
Презентация на тему Песня… про купца Калашникова  675474
675474 Открытие отрицательных чисел
Открытие отрицательных чисел Отраслевые решения «1С» для сельского хозяйства и пищевой промышленности в ВУЗЫ
Отраслевые решения «1С» для сельского хозяйства и пищевой промышленности в ВУЗЫ Подготовка крестьянской реформы
Подготовка крестьянской реформы