Содержание
- 2. Теоретическая физика Задача теоретической физики: понять фундаментальные законы устройства мира. Цель доклада: немного рассказать о методах
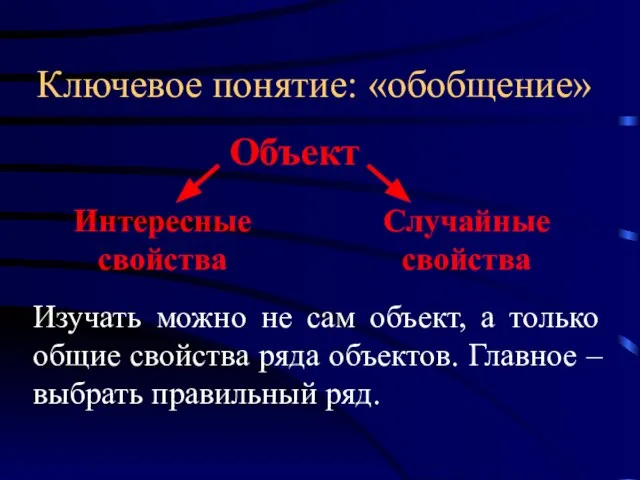
- 3. Ключевое понятие: «обобщение» Изучать можно не сам объект, а только общие свойства ряда объектов. Главное –
- 4. Пример: сфера Как стать лучшим в мире специалистом по сферам? ?
- 5. Специалист-экспериментатор Изготовление идеально сферических тел из разных материалов Изучение сил сопротивления при движении сферы в вязких
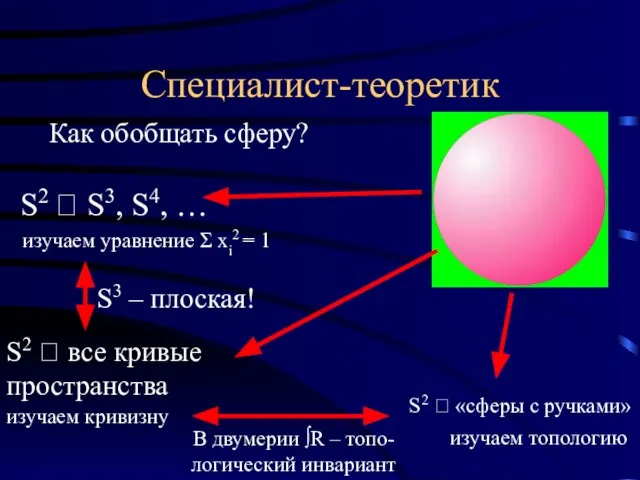
- 6. Специалист-теоретик Как обобщать сферу? S2 ? S3, S4, … изучаем уравнение Σ xi2 = 1 S2
- 7. Вывод Чтобы понять, как устроен наш мир, нужно изучать другие миры, похожие на наш. А теперь
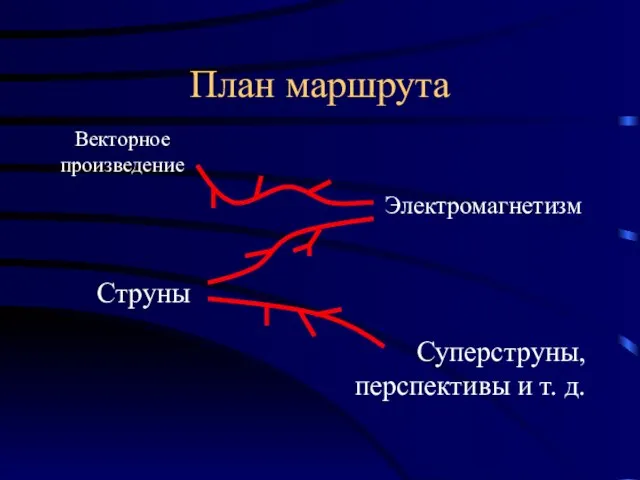
- 8. План маршрута Векторное произведение Электромагнетизм Струны Суперструны, перспективы и т. д.
- 9. Векторное произведение Что это такое на самом деле? Магнитное поле: Вращение: Сколько параметров в d-мерии? d
- 10. Удивление Магнитное поле – не вектор! Правильный взгляд: Вопрос: что такое правильные уравнения Максвелла?
- 11. Уравнения Максвелла - 1 Проблема спрятана здесь: Нужно понять, что такое div, rot, grad…
- 12. Div, rot, grad – 1 Свойства: div rot = 0 rot grad = 0 Разные формулы
- 13. Div, rot, grad – 2 «Правильный» взгляд:
- 14. Свойства оператора d d – «оператор де Рама» «Теорема семи авторов» : d2 = 0 (Ньютона,
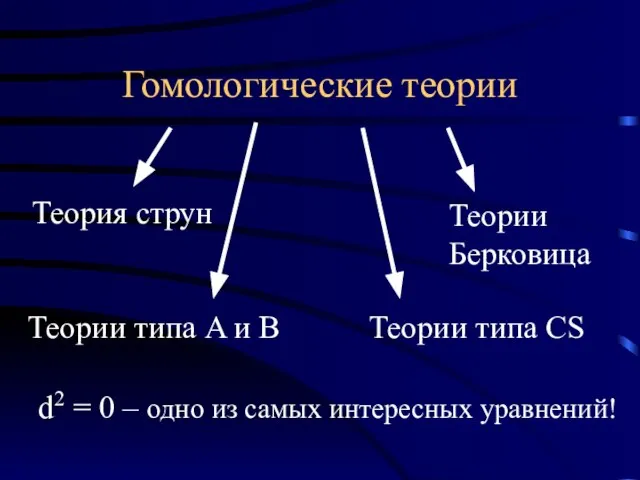
- 15. Гомологические теории Теория струн Теории типа A и B Теории типа CS Теории Берковица d2 =
- 16. Оператор «*» У нас возникал оператор из Ωk в Ωn-k . Это – «звездочка Ходжа». Ω
- 17. Уравнения Максвелла – 2 Fμν -- матрица электромагнитного поля F = Fμν dx μ dx ν
- 18. В пустом пространстве уравнения М.: Замена переводит уравнения в себя! В (3+1)-мерии это есть . Дуальность
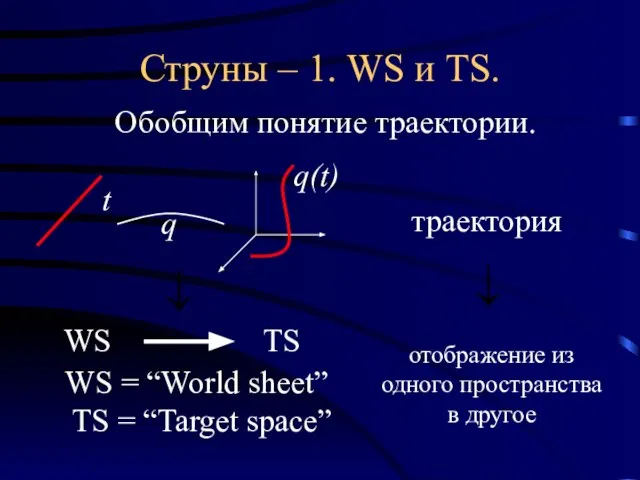
- 19. Струны – 1. WS и TS. Обобщим понятие траектории. t q q(t) WS TS WS =
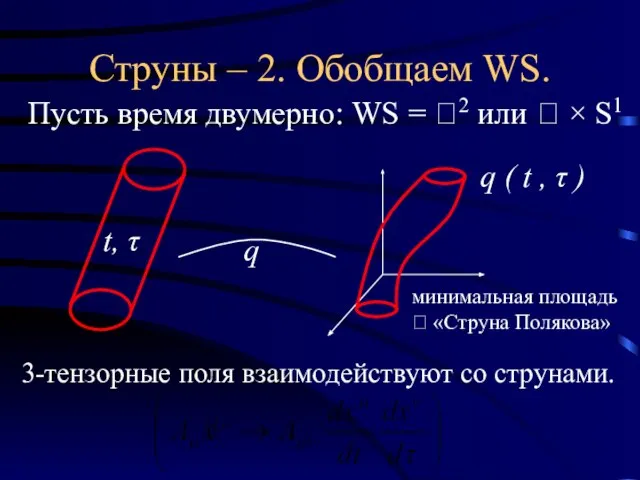
- 20. Струны – 2. Обобщаем WS. Пусть время двумерно: WS = 2 или × S1 q
- 21. Какие бывают TS? Простейший вариант – «система со связями» (например, обычный маятник – это TS =
- 22. Супер-… ? Это были просто струны («бозонные»). А что такое «суперструны»?.. Оказывается, есть целая «супернаука»: про
- 23. Суперпространство – 1 Еще одно обобщение пространства: Добавим антикоммутирующие переменные θ μ . θ μ θ
- 24. Суперпространство – 2 «Нечетное преобразование Фурье»: Дифференцирование: Интегрирование: Это – звездочка Ходжа!
- 25. Континуальный интеграл: ∫x Еще одно обобщение интеграла – интеграл по всем траекториям из x в y.
- 26. «Перспективы» – 1: BV BV-формализм – возможно, позволит построить «хорошую» теорию гравитации. Главный герой – оператор
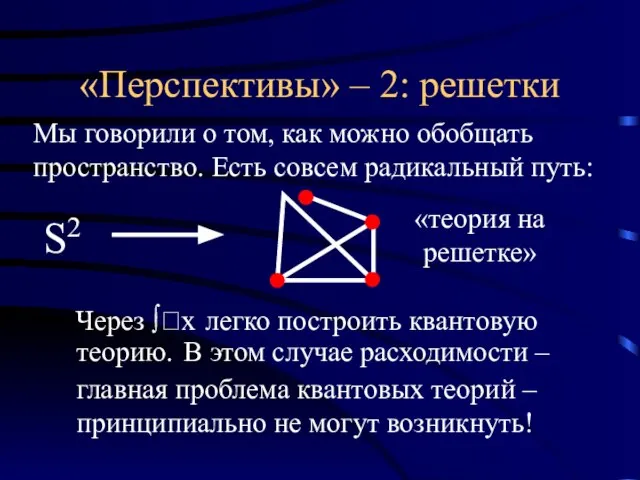
- 27. «Перспективы» – 2: решетки Мы говорили о том, как можно обобщать пространство. Есть совсем радикальный путь:
- 29. Скачать презентацию



















 Отдельные виды договорных отношений в жилищном праве
Отдельные виды договорных отношений в жилищном праве Организация велостоянки для гимназии №1
Организация велостоянки для гимназии №1 О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го
О компании Основным направлением деятельности группы компаний InstaForex является предоставление услуг online-трейдинга клиентам с 2007 го Урок русского языка в 6 классе по теме: «Правописание сложных существительных»
Урок русского языка в 6 классе по теме: «Правописание сложных существительных» Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании
Ярмарка инноваций в образовании Секция: Инновации в дошкольном образовании Невидимые нити в весеннем лесу (2 класс)
Невидимые нити в весеннем лесу (2 класс) Игрушки из носочков своими руками №7
Игрушки из носочков своими руками №7 Введение в специальность
Введение в специальность Герцог Ами
Герцог Ами Трение. Вредно или полезно
Трение. Вредно или полезно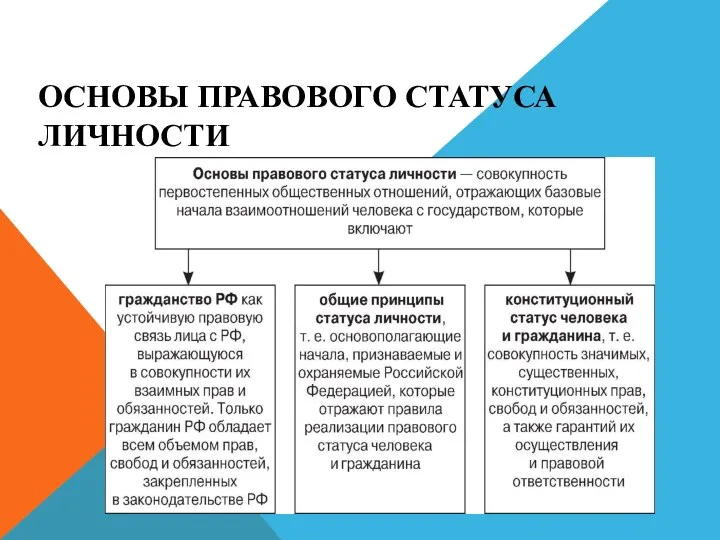 Правовой статус личности. Гражданство РФ
Правовой статус личности. Гражданство РФ Социальная психология
Социальная психология Презентация на тему АФАНАСИЙ НИКИТИН
Презентация на тему АФАНАСИЙ НИКИТИН  Теория обучения
Теория обучения Презентация на тему Our Environment (Наша окружающая среда)
Презентация на тему Our Environment (Наша окружающая среда) Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС)
Универсальный программный комплекс для информационно-аналитического сопровождения (УПК ИАС) Презентация по информатике на тему: «Устройства вывода информации, монитор.»
Презентация по информатике на тему: «Устройства вывода информации, монитор.» Круглопольское сельское поселение
Круглопольское сельское поселение Прайс косметологических услуг салона Забота о вас
Прайс косметологических услуг салона Забота о вас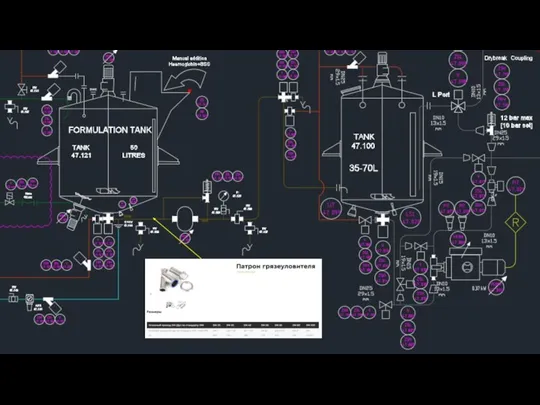 Патрон грязеуловителя
Патрон грязеуловителя Назначение изделия и его описание
Назначение изделия и его описание Планирование и организация процесса закупок материальных ресурсов промышленного предприятия
Планирование и организация процесса закупок материальных ресурсов промышленного предприятия Распространение объектно-ориентированного подхода на информационную безопасность
Распространение объектно-ориентированного подхода на информационную безопасность Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк.
Определите тему произведения по моделям Дмитрий Наркисович Мамин - Сибиряк. Пейзаж в графике
Пейзаж в графике Рогожка. Коллекция однотонных штор
Рогожка. Коллекция однотонных штор _Презентация. Предоставление
_Презентация. Предоставление Презентация
Презентация