Некоторые именные теоремы о треугольниках

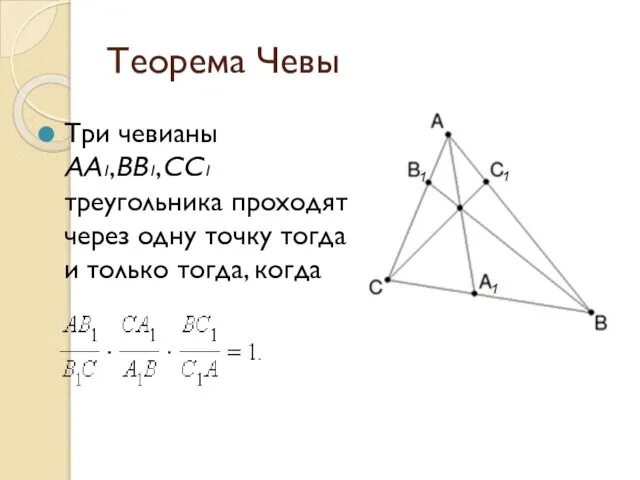
Теорема Чевы
Три чевианы AA1,BB1,CC1 треугольника проходят через одну точку тогда и только тогда, когда

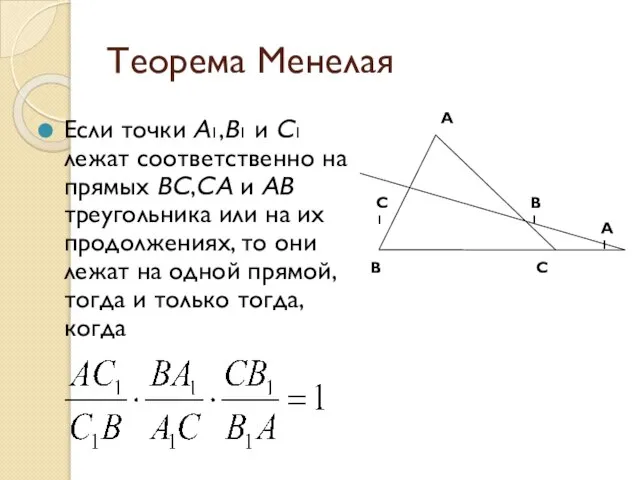
Теорема Менелая
Если точки A1,B1 и C1 лежат соответственно на прямых BC,CA и AB треугольника или на их продолжениях, то они лежат на одной прямой, тогда и только тогда, когда

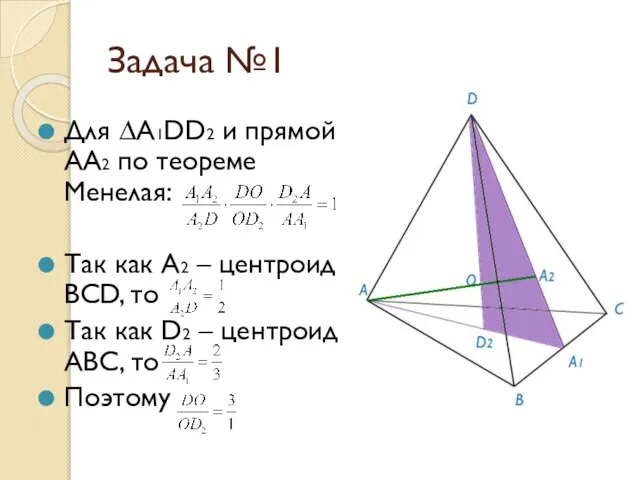
Задача №1
Доказать, что отрезки, соединяющие вершины тетраэдра с центроидами противоположных граней, пересекаются в одной точке и делятся ей в отношении 3:1, считая от вершин.

Задача №1
Для ∆A1DD2 и прямой AA2 по теореме Менелая:
Так как A2 – центроид BCD, то
Так как D2 – центроид ABC, то
Поэтому

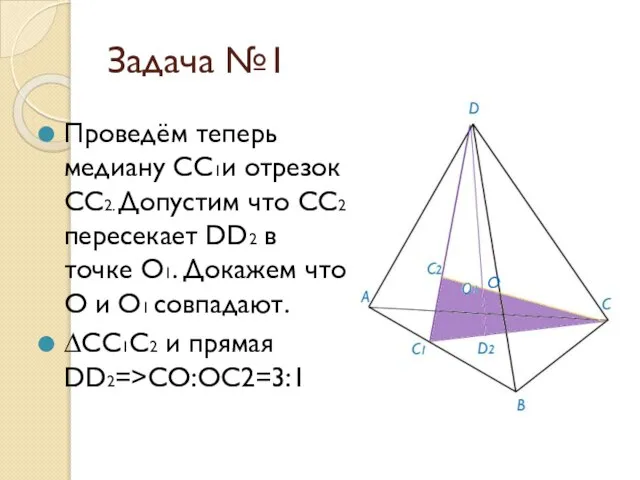
Задача №1
Проведём теперь медиану CC1и отрезок CC2. Допустим что CC2 пересекает DD2 в точке O1. Докажем что О и О1 совпадают.
∆СС1С2 и прямая DD2=>CO:OC2=3:1

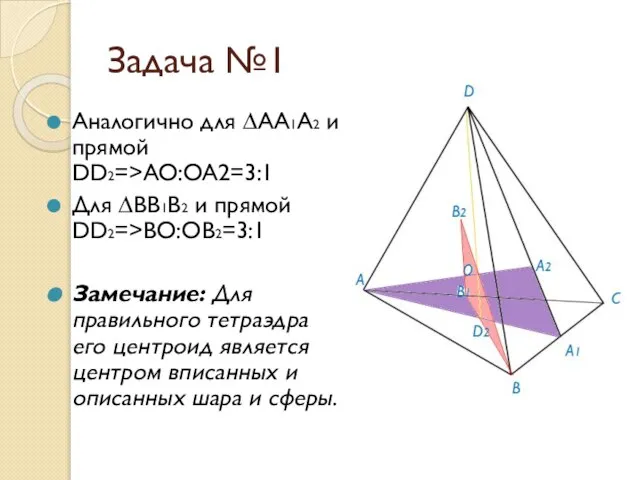
Задача №1
Аналогично для ∆АА1А2 и прямой DD2=>AO:OA2=3:1
Для ∆BB1B2 и прямой DD2=>BO:OB2=3:1
Замечание: Для правильного тетраэдра его центроид является центром вписанных и описанных шара и сферы.

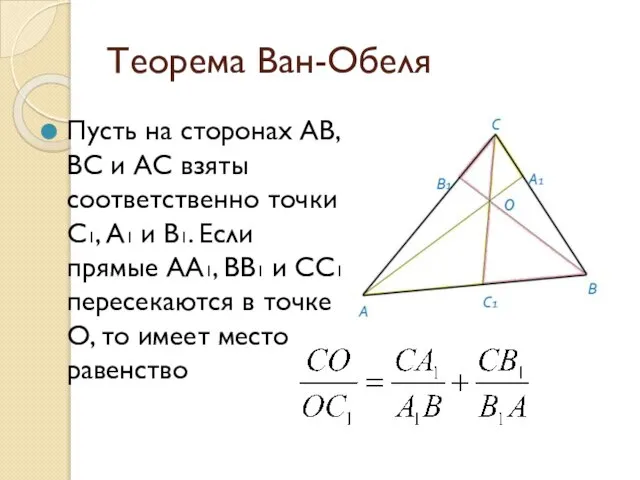
Теорема Ван-Обеля
Пусть на сторонах АВ, ВС и АС взяты соответственно точки С1, А1 и В1. Если прямые АА1, ВВ1 и СС1 пересекаются в точке О, то имеет место равенство

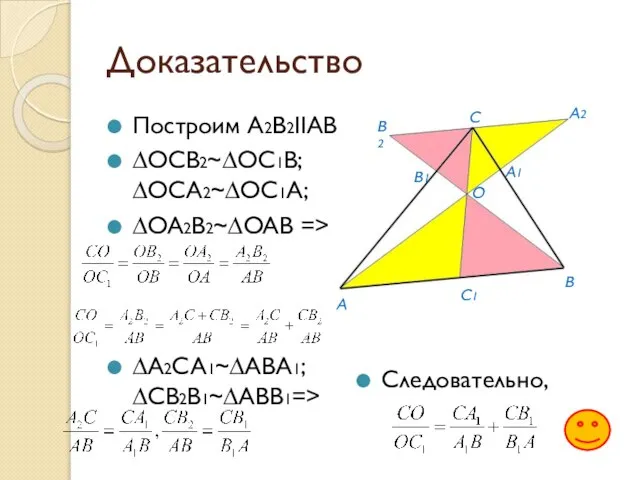
Доказательство
Построим А2В2ΙΙАВ
∆OCB2~∆OC1B; ∆OCA2~∆OC1A;
∆OA2B2~∆OAB =>
∆A2CA1~∆ABA1; ∆CB2B1~∆ABB1=>
Следовательно,

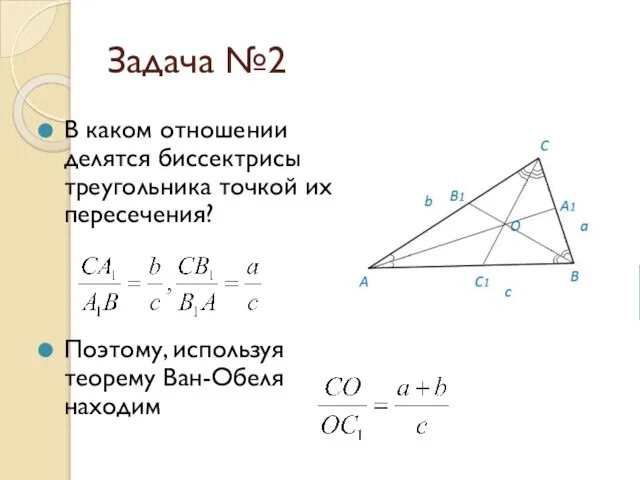
Задача №2
В каком отношении делятся биссектрисы треугольника точкой их пересечения?
Поэтому, используя теорему Ван-Обеля находим

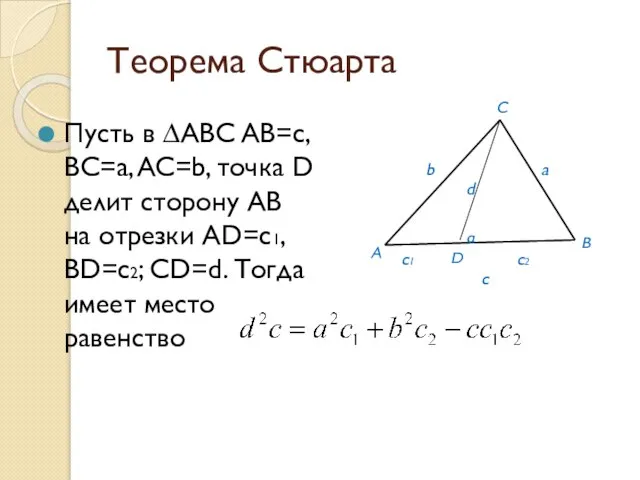
Теорема Стюарта
Пусть в ∆ABC AB=c, BC=a, AC=b, точка D делит сторону AB на отрезки AD=c1, BD=c2; CD=d. Тогда имеет место равенство

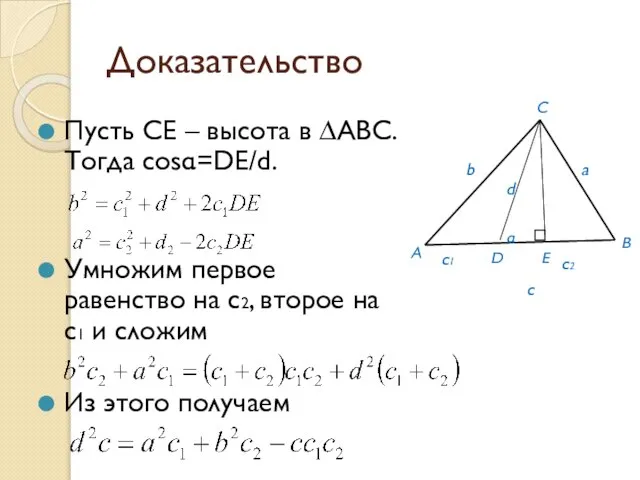
Доказательство
Пусть CE – высота в ∆АВС. Тогда cosα=DE/d.
Умножим первое равенство на с2, второе на с1 и сложим
Из этого получаем

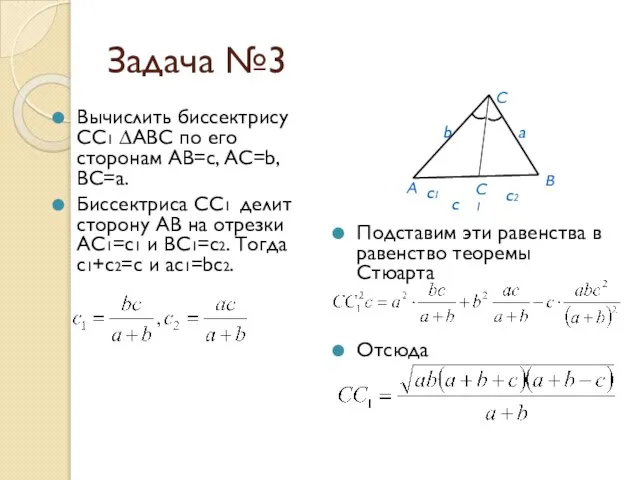
Задача №3
Вычислить биссектрису СС1 ∆АВС по его сторонам АВ=с, АС=b, ВС=а.
Биссектриса СС1 делит сторону АВ на отрезки АС1=с1 и ВС1=с2. Тогда с1+с2=с и ac1=bc2.
Подставим эти равенства в равенство теоремы Стюарта
Отсюда
c

Спасибо за внимание!