Некоторые следствия из аксиом

А
В
С
Д
Р
Е
К
М
А
В
С
Д
А1
В1
С1
Д1
Q
P
R
К
М
2) №1 (в,г); 2(б,д). Назовите по рисунку:
в) точки, лежащие в плоскостях АДВ и ДВС; г) прямые по которым пересекаются плоскости АВС и ДСВ, АВД и СДА, РДС и АВС.
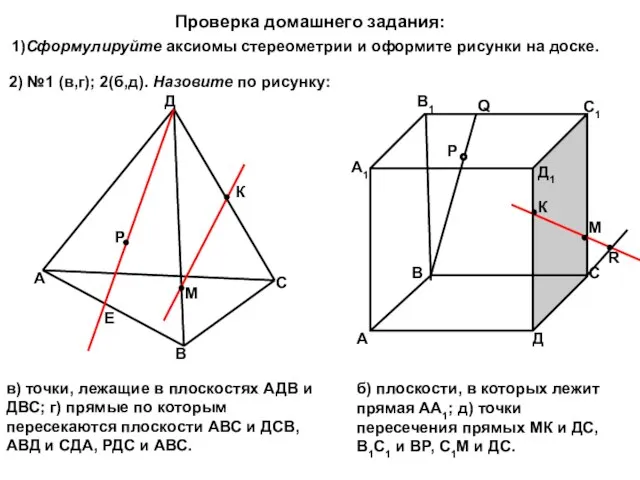
б) плоскости, в которых лежит прямая АА1; д) точки пересечения прямых МК и ДС, В1С1 и ВР, С1М и ДС.
Проверка домашнего задания:
1)Сформулируйте аксиомы стереометрии и оформите рисунки на доске.

Теорема 1. Через прямую и не лежащую на ней точку проходит плоскость и притом только одна.
Дано:
а, М ¢ а
Доказать:
(а, М) с α
α- единственная
а
М
α
Доказательство :
1. Р, О с а; {Р,О,М} ¢ а
Р
О
По аксиоме А1: через точки Р, О, М проходит плоскость .
По аксиоме А2: т.к. две точки прямой принадлежат плоскости, то и вся прямая принадлежит этой плоскости, т.е. (а, М) с α
2. Любая плоскость проходящая через прямую а и точку М проходит через точки Р, О, и М, значит по аксиоме А1 она – единственная. Ч.т.д.
Некоторые следствия из аксиом:

Теорема 2. Через две пересекающиеся прямые проходит плоскость, и притом только одна.
Дано:
а∩b
Доказать:
1. (а∩b) с α
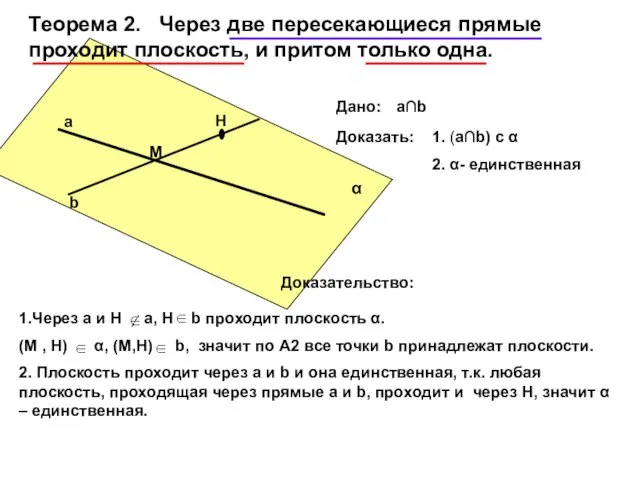
2. α- единственная
а
b
М
Н
α
Доказательство:
1.Через а и Н а, Н b проходит плоскость α.
(М , Н) α, (М,Н) b, значит по А2 все точки b принадлежат плоскости.
2. Плоскость проходит через а и b и она единственная, т.к. любая плоскость, проходящая через прямые а и b, проходит и через Н, значит α – единственная.

Решить задачу № 6
А
В
С
α
Три данные точки соединены попарно отрезками. Докажите, что все отрезки лежат в одной плоскости.
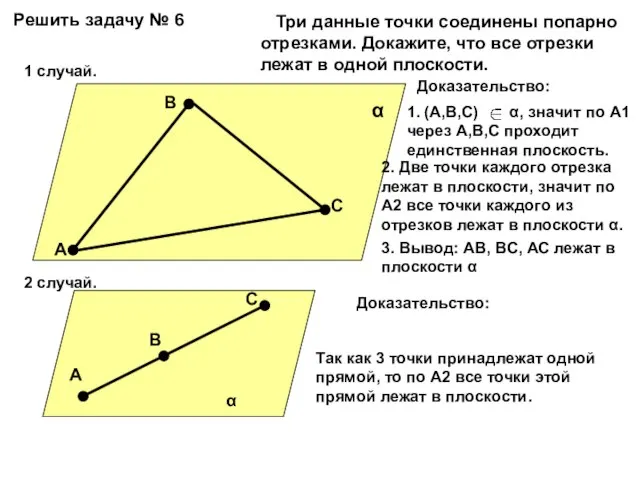
Доказательство:
1. (А,В,С) α, значит по А1 через А,В,С проходит единственная плоскость.
2. Две точки каждого отрезка лежат в плоскости, значит по А2 все точки каждого из отрезков лежат в плоскости α.
3. Вывод: АВ, ВС, АС лежат в плоскости α
1 случай.
А
В
С
α
2 случай.
Доказательство:
Так как 3 точки принадлежат одной прямой, то по А2 все точки этой прямой лежат в плоскости.

Задача.
А
В
С
Д
М
О
АВСД – ромб, О – точка пересечения его диагоналей, М – точка пространства, не лежащая в плоскости ромба. Точки А, Д, О лежат в плоскости α.
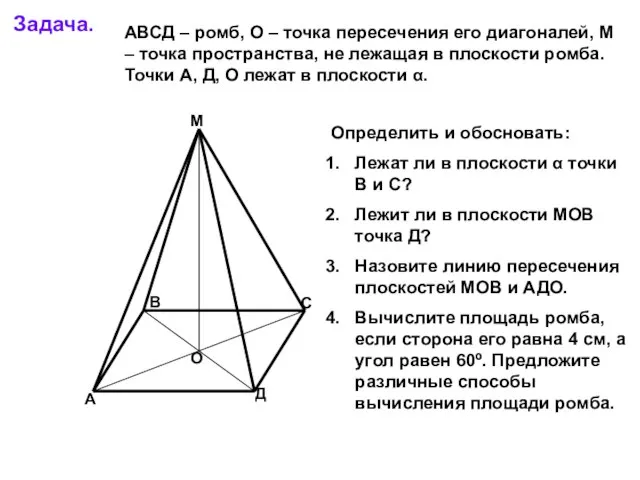
Определить и обосновать:
Лежат ли в плоскости α точки В и С?
Лежит ли в плоскости МОВ точка Д?
Назовите линию пересечения плоскостей МОВ и АДО.
Вычислите площадь ромба, если сторона его равна 4 см, а угол равен 60º. Предложите различные способы вычисления площади ромба.

А
В
С
Д
60º
4
4
4
4
SАВСД = АВ · АД · sinA
SАВСД = (ВД · АС):2
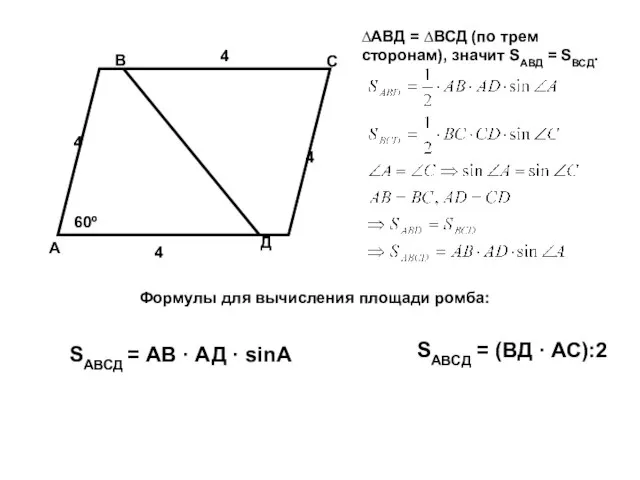
Формулы для вычисления площади ромба:
∆АВД = ∆ВСД (по трем сторонам), значит SАВД = SВСД.