НЕРАВЕНСТВА

СОДЕРЖАНИЕ:
1. Объединение и пересечение множеств.
2. Числовые промежутки.
3. Решение неравенств с одной переменной.
4. Решение систем неравенств с одной переменной.

Пересечение множеств:
Пересечением двух множеств называют множество, состоящее из всех общих элементов этих множеств.
Например:
А= { 2;4;6;8;10;12;14;16;18;20 }
В= { 3;6;9;12;15;18 }
А∩В=С={6;12;18 }

Объединением двух множеств называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств:
Например:
А={2; 4; 6; 8; 10; 12; 14; 16; 18;20}
В={3; 6; 9; 12; 15; 18}
АUВ=D={2;3 ;4; 6; 8; 9; 10; 12; 14; 15; 16; 18; 20}
Объединение множеств:

А = {1, 4, 9, 16, 25, 36, 49, 64, 81,100}
В = {1, 8, 27, 64}
А ∩ В =
А U В =
Найдите пересечение и объединение множеств:

Числовые промежутки:

Числовые промежутки:

1.Изобразите на координатной прямой промежуток:
а) (-1; 5)
б) (-4; 3]
в) (- ∞; 4)
г) (-5; +∞)
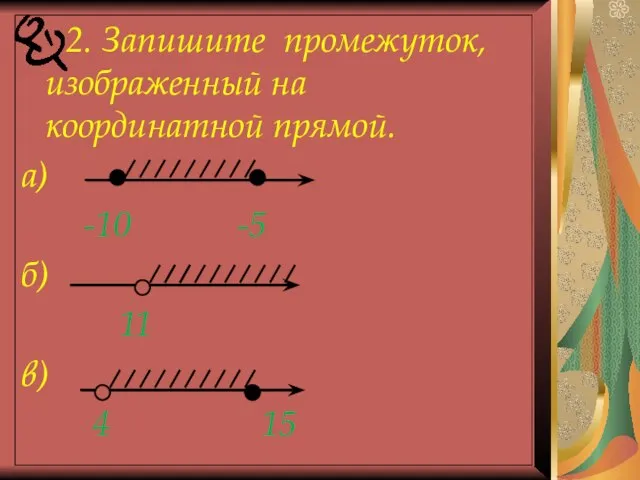
д) [-3; 9]

2. Запишите промежуток, изображенный на координатной прямой.
а)
-10 -5
б)
11
в) 4 15

3. Какие целые числа принадлежат промежутку:
а) ( -2,1 ; 3 )
б) ( 6 ; 9 ]
в) [ -12 ; -1 ]
г) [ 0,9 ; 6,5 ]

4. Используя координатную прямую, найдите пересечение промежутков:
а) ( - 6 ; 5 ) и ( 0 ; 12 )
б) [ - 2 ; 7 ] и ( 3 ; 9 )
в) ( - ∞ ; 8 ) и ( - 6 ; + ∞)
г) ( 1 ; + ∞ ) и ( 9 ; + ∞ )

Линейное неравенство с одной переменной - это неравенство вида
ах > в или ах < в, где а и в некоторые числа.
Решением неравенства с одной переменной называется значение переменной, которое обращает его в верное числовое равенство.

Например: 4х -11 > 5
х = 1 4∙1 -11>5
-7>5 - неверно
Значит х=1 не является решением неравенства.
х = 5 4∙5 -11>5
9>5 – верно
Значит х=5 является решением неравенства.

Решить неравенство –
значит найти все его
решения или доказать, что их нет.

Если из одной части неравенства перенести в другую слагаемое с противоположным знаком, то получится равносильное ему неравенство.
Если обе части неравенства умножить или разделить на одно и то же положительное число, то получится равносильное ему неравенство.
Если обе части неравенства умножить или разделить на одно и то же отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное ему неравенство.
При решении неравенств используют следующие свойства:

Неравенства, имеющие одни и те же решения. называются равносильными.
Неравенства, не имеющие решений, также считают равносильными.

Решим неравенство
16х > 13х + 45
16х – 13х > 45
3х > 45
х >15
15
Ответ: ( 15 ; +∞ )
Приведем примеры решения
неравенств:

Решим неравенство
15х – 23(х + 1) > 2х + 11
15х – 23х – 23 > 2х + 11
15х -23х – 2х > 11 + 23
-10х > 34
х < -3,4
-3,4
Ответ: (-∞; - 3,4)

Решите неравенство и изобразите множество его решений на координатной прямой:
а) х+12<6 б) х-2,7≥0
в) 2х>14 г) -5х<30
д) 8+5у>1-у е) 17-у≤22

Решением системы неравенств
с одной переменной называется значение переменной, при котором
верно каждое из неравенств системы.
Решить систему – значит найти все её решения или доказать, что их нет.