Структура экзамена по математике

Вопросы и задания
Всего заданий: 18
Из них по типу заданий:
Часть В — 12
Часть С — 6
Максимальный первичный балл
за работу: 30
Общее время выполнения работы:
240 мин.
Минимальное количество баллов по ЕГЭ в 2010 году – 21.

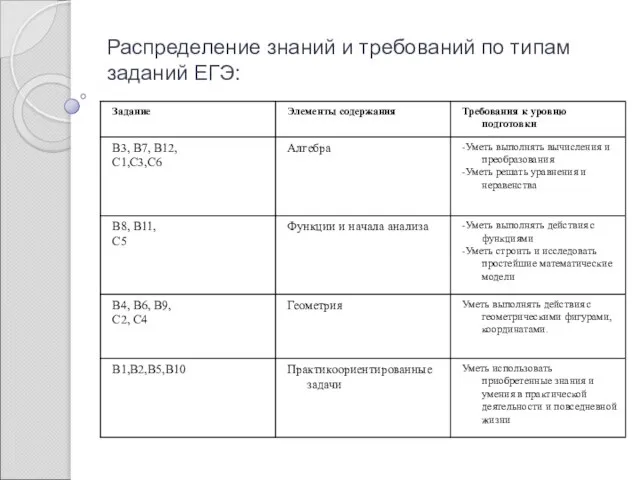
Распределение знаний и требований по типам заданий ЕГЭ:

Полезные сайты
http://fipi.ru
http://mathege.ru – открытый банк задач
Главная задача открытого банка заданий ЕГЭ по математике — дать представление о том, какие задания будут в вариантах экзамена по математике в 2011 году, и помочь выпускникам сориентироваться при подготовке к экзамену.
Задачи открытого банка помогут будущим выпускникам повторить (освоить) школьный курс математики, найти в своих знаниях слабые места и ликвидировать их до экзамена. Задачи В1–В12 представлены заданиями, аналогичными экзаменационным (отличия — только в числовых параметрах), кроме того, на каждой позиции представлены задания и попроще, и посложнее реальных.
http://alexlarin.narod.ru
http://alleng.ru
http://statgrad.mioo.ru
http://www.ctege.org
http://ege.edu.ru

Открытый банк задач
Задания В1.
Решение текстовых задач.
Всего предлагается 55 различных видов задач.
http://mathege.ru

№1. Сырок стоит 7 руб. 20 коп. Какое наибольшее число сырков можно купить на 60 рублей?
Решение:
1 способ:
60 руб. = 6000 коп.
7 руб. 20 коп. = 720 коп.
6000:720 ≈ 8,(3)
2 способ:
60 руб.
7 руб. 20 коп. = 7,2 руб.
60:7,2 ≈ 8,(3)
Ответ: 8
Помнить!
Округляем в меньшую сторону до целых, т.к. в магазине бесплатно товар не дают и часть сырка купить нельзя.

№2. Теплоход рассчитан на 750 пассажиров и 25 членов экипажа. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды.
Решение:
750 + 25 = 775 (человек)
775:70 = 11 (5 остаток)
Помнить!
Округляем в большую сторону до целых, т. к. людей в беде бросать нельзя.
В вопросе есть выражение «наименьшее число шлюпок». Оно может привести к затруднениям в рассуждениях. Это выражение говорит всего лишь о том, что необходимо брать столько шлюпок, сколько требуется и не больше. Например, взяв 1000 шлюпок, всех можно разместить, но где здравый смысл?
Ответ: 12

№3. Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?
Решение:
100 +20=120% цена горшка с наценкой.
120 руб. – 100 % «Перекрестное» правило: (свойство членов пропорции)
x руб. – 120%
100 x= 120*120
100x=14400
x = 144 (руб.) – цена горшка с наценкой.
Далее как в задаче №1. 1000:144 = 6,9 (4)
Ответ: 6
Повторить тему «Проценты»!
Помнить! Первоначальная величина - 100%

№4. Футболка стоила 800 рублей. После снижения цены она стала стоить 680 рублей. На сколько процентов была снижена цена на футболку?
Решение: Исходная величина 800рублей – это 100%.
800 руб. – 100%
680 руб. – x
Помним о «перекрестном» правиле.
800x = 680∙ 100
x = 680∙100 ∕ 800 = 85 (%) – новая цена
Ответ: 15
Читаем вопрос!
100 – 85 = 15 (%) – снижена цена.
На сколько процентов была снижена цена на футболку?

Открытый банк задач.
http://mathege.ru
Задания В2. Чтение графиков.
Всего предлагается 31 вид задач.

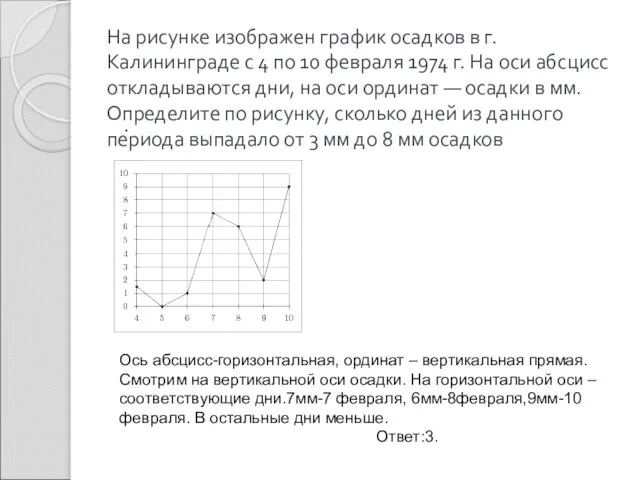
На рисунке изображен график осадков в г.Калининграде с 4 по 10 февраля 1974 г. На оси абсцисс откладываются дни, на оси ординат — осадки в мм. Определите по рисунку, сколько дней из данного периода выпадало от 3 мм до 8 мм осадков
.
Ось абсцисс-горизонтальная, ординат – вертикальная прямая.Смотрим на вертикальной оси осадки. На горизонтальной оси – соответствующие дни.7мм-7 февраля, 6мм-8февраля,9мм-10 февраля. В остальные дни меньше.
Ответ:3.

Открытый банк задач
Задания В3. Решение уравнений.
Всего предлагается 47 различных видов задач.
http://mathege.ru

Найти корень уравнения
Решение:
Ответ: – 124
В логарифмических уравнениях помним про ОДЗ!
4 – x > 0
x < 4
В данном уравнении нет посторонних корней.

Найти корень уравнения:
Решение:
Ответ: -1
Найти корень уравнения:
Решение:
Ответ: 4

Найти корень уравнения
Ответ: 0,3
Решение:
Вспомнить «перекрестное» правило!
Помним про ОДЗ!

Для решения заданий В3 повторить:
Все основные формулы, связанные с логарифмами
Методы решения простейших логарифмических и показательных уравнений
Решение дробно-рациональных уравнений.

Открытый банк задач
Задания В4.
Геометрические задачи.
Всего предлагается 455 различных видов задач.
http://mathege.ru

Для решения заданий В4 повторить:
Определение синуса, косинуса, тангенса и котангенса острого угла прямоугольного треугольника.
Основное тригонометрическое тождество.
Теорему Пифагора: квадрат гипотенузы равен сумме квадратов катетов.

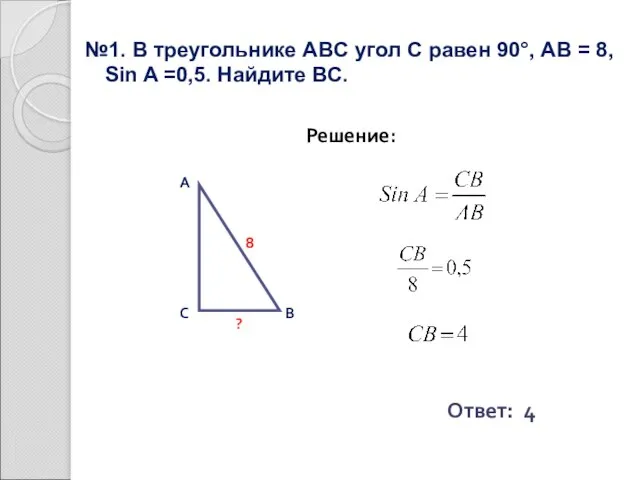
№1. В треугольнике ABC угол С равен 90°, AВ = 8, Sin A =0,5. Найдите ВС.
Решение:
Ответ: 4

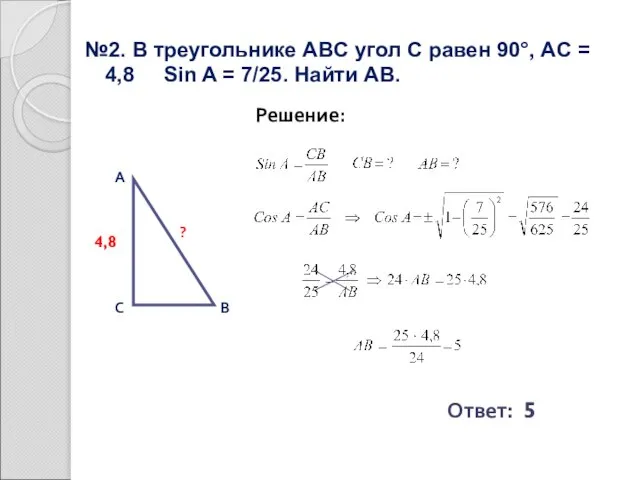
№2. В треугольнике ABC угол С равен 90°, AC = 4,8 Sin A = 7/25. Найти АВ.
Решение:
Ответ: 5

Открытый банк задач
http://mathege.ru
Задания В6.
Геометрические задачи на нахождение площади многоугольников.
Предлагается 223 вида задач.

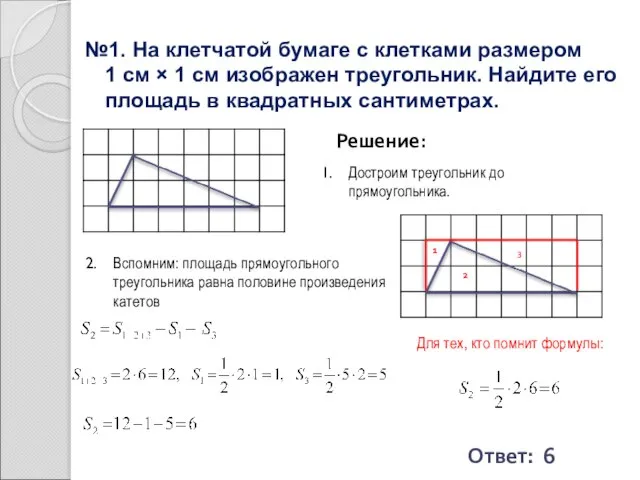
№1. На клетчатой бумаге с клетками размером 1 см × 1 см изображен треугольник. Найдите его площадь в квадратных сантиметрах.
Решение:
Ответ: 6
Достроим треугольник до прямоугольника.
Вспомним: площадь прямоугольного треугольника равна половине произведения катетов
Для тех, кто помнит формулы:

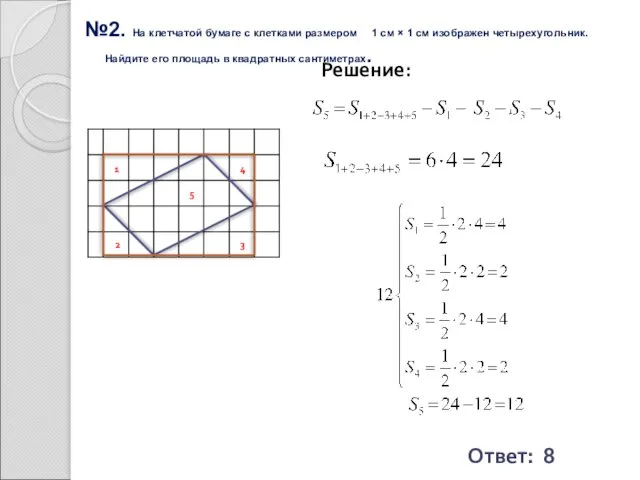
№2. На клетчатой бумаге с клетками размером 1 см × 1 см изображен четырехугольник. Найдите его площадь в квадратных сантиметрах.
Решение:
Ответ: 8

Открытый банк задач
http://mathege.ru
Задания В5. «Работа с таблицами»
Всего предлагается 18 видов задач.

Для транспортировки 45 тонн груза на 1300 км можно воспользоваться услугами одной из трех фирм-перевозчиков. Стоимость перевозки и грузоподъемность автомобилей для каждого перевозчика указана в таблице. Сколько рублей придется заплатить за самую дешевую перевозку?

Решение:
41600*13=540 800
53300*9=479 700
123500*4=494 000
Ответ: 479 700

Открытый банк задач
Задания В7. «Преобразования выражений»
Всего предлагается 171 вид задач.
http://mathege.ru

Найти значение выражения:
Найти значение выражения:
Найти значение выражения:
Найти значение выражения:

Найти значение выражения:

Открытый банк задач
Задания В8. Производная.
Всего предлагается 33 вида задач.
http://mathege.ru

При решении данных задач помним:
1)f’ (x) используем, когда в задаче задана функция y = f(x).
Мы можем найти ее производную.
Или изображен график производной данной функции.
Можно найти ее значение в какой-то точке.
2)tg α используем, когда изображена касательная.
3)коэффициент k, когда задано уравнение касательной прямой
y = kx+b
4)y=f(x) – убывает => f’(x) ≤ 0, график функции y = f’ (x)
лежит ниже оси OX.
5)y=f(x) – возрастает <= f’(x) ≥ 0, график функции y = f’ (x) лежит выше оси OX.
6)Точки экстремума – это те точки, в которых производная равна нулю. То есть те точки, в которых график функции y = f’(x) пересекает ось OX

При решении данных задач помним:
Помним, что tg α – это тангенс угла наклона касательной к положительному направлению оси Ох
Находим (строим) на рисунке прямоугольный треугольник с углом α. Находим тангенс угла α (рис 1) или тангенс угла β (рис.2). Но помним, что найти необходимо tg α = - tg β.

Прямая у=7х-5 параллельна касательной к графику функции Найдите абсциссу точки касания.
Основная формула f’ (x) =tga =k
Т.к. задана функция y = f(x), можно найти ее производную. f’ (x)=2х+6
Т.к. касательная параллельна прямой у=7х-5, то k=7.
Следовательно, f’ (x) = k, т.е.2х+6=7. Решаем данное уравнение.
2х+6=7
2х=1
Х=0,5
Ответ: 0,5

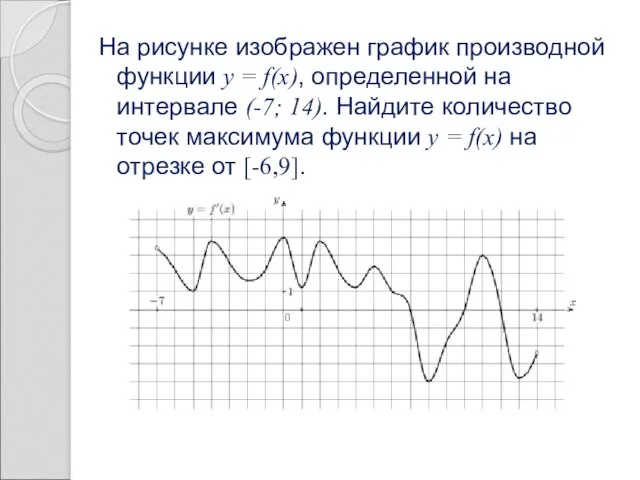
На рисунке изображен график производной функции y = f(x), определенной на интервале (-7; 14). Найдите количество точек максимума функции y = f(x) на отрезке от [-6,9].

Решение.
В точках максимума(минимума) производная принимает значение равное нулю. В этих точках график производной пересекает ось Ох. На рисунке таких точек две, но в заданный отрезок попадает только одна. Это точка с координатой (7;0).
Ответ:1.

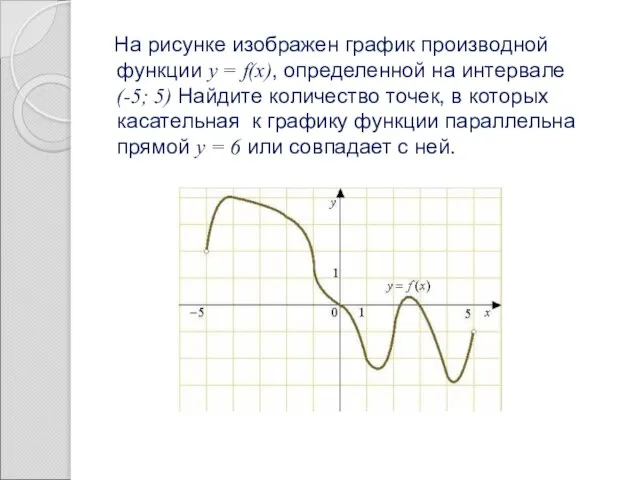
На рисунке изображен график производной функции y = f(x), определенной на интервале (-5; 5) Найдите количество точек, в которых касательная к графику функции параллельна прямой y = 6 или совпадает с ней.

Решение.
Основная формула: f’ (x) =tga =k
Нам дана прямая у=6, коэффициент к=0, т.к. отсутствует слагаемое, содержащее переменную х. Касательная параллельна данной прямой, угловой коэффициент касательной (k) будет тоже равен нулю. Из основной формулы видно, что f’ (x) = k. Т.к. k =0, то и f’ (x) = 0. Производная равна нулю в тех точках, в которых ее график пересекает ось Ох. Таких точек на указанном промежутке три.
Ответ: 3.

Открытый банк задач
Задания В11. «Исследования функций на наибольшее (наименьшее) значение»
Всего предлагается 126 видов задач
http://mathege.ru

Для решения задач необходимо повторить:
Правила нахождения производных.
Алгоритм:
Найти производную.
Приравнять к нулю. Решить получившиеся уравнение.
Выбрать корни уравнения, которые попадают в заданный отрезок.
Найти значение функции на концах отрезка и в нулях производной, которые попали в отрезок.
Ответить на вопрос задачи.