Неравенство треугольника.

Способы расположения трех точек на плоскости.
1. Все три точки совпадают.
.
А
В
.
С
.
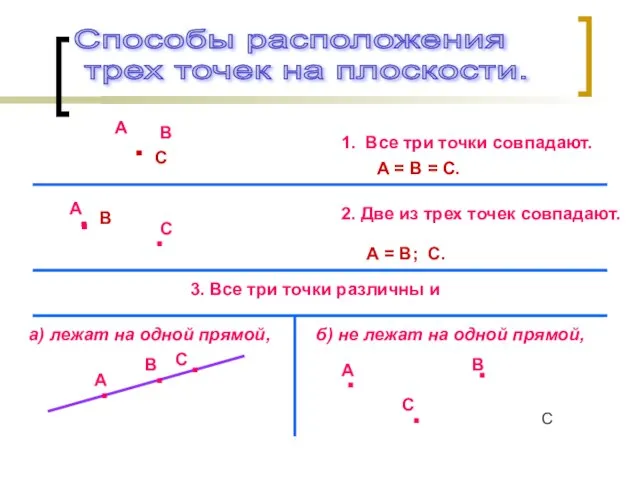
А = В = С.
2. Две из трех точек совпадают.
А
В
С
.
.
.
А = В; С.
3. Все три точки различны и
а) лежат на одной прямой,
б) не лежат на одной прямой,
.
.
.
А
В
С
С
.
.
.
А
В
С
.

Теорема.
Каковы бы ни были три точки, расстояние между любыми двумя из этих точек не больше суммы расстояний от них до третьей точки.
Доказательство.
1. Если все три точки совпадают, то АВ = ВС = АС = 0, - условие теоремы выполняется
2. Две из трех точек совпадают (А=В), то АВ = 0, ВС = АС, - условие теоремы также выполняется.
3. Все три точки различны и лежат на одной прямой.
А
В
С
.
.
.
В этом случае одна из трех точек лежит между двумя другими (свойство взаимного расположения точек на прямой),
тогда по свойству измерения отрезков АС = АВ = ВС,
т. е. условие теоремы выполняется.