Содержание
- 2. Оглавление Лента Мёбиуса Бутылка Клейна Невозможный треугольник Невозможный трезубец Невозможная лестница Кольца Борромео Ссылки
- 3. Лента Мёбиуса Лента Мебиуса - трехмерная поверхность, имеющая только одну сторону и одну границу, обладающая математическим
- 4. Бутылка Клейна Бутылка Клейна - это математическая неориентируемая поверхность, в которой неразличимы внутренняя и внешняя стороны.
- 5. Невозможный треугольник В 1934 году Оскар Реутерсвард создал первый невозможный треугольник, составленный из серии кубиков. Хотя
- 6. Невозможный трезубец Среди всех невозможных фигур особое место занимает невозможный трезубец. Если закрыть рукой верхнюю часть
- 7. Невозможная лестница Невозможная лестница - одна из базовых невозможных фигур. Ее еще иногда называют бесконечной лестницей.
- 8. Кольца Борромео Кольца Борромео - одна из известных невозможных фигур, имеющая древнюю историю. Эта фигура основана
- 10. Скачать презентацию
Слайд 2Оглавление
Лента Мёбиуса
Бутылка Клейна
Невозможный треугольник
Невозможный трезубец
Невозможная лестница
Кольца Борромео
Ссылки
Оглавление
Лента Мёбиуса
Бутылка Клейна
Невозможный треугольник
Невозможный трезубец
Невозможная лестница
Кольца Борромео
Ссылки
Слайд 3Лента Мёбиуса
Лента Мебиуса - трехмерная поверхность, имеющая только одну сторону и одну
Лента Мёбиуса
Лента Мебиуса - трехмерная поверхность, имеющая только одну сторону и одну

границу, обладающая математическим свойством неориентируемости. Она была открыта независимо одновременно двумя математиками из Германии Августом Фердинандом Мебиусом и Иоганном Бенедиктом Листингом в 1858 году.
Одна из базовых невозможных фигур, невозможный треугольник, может быть представлен как лента Мебиуса, если сгладить некоторые его грани. При этом получится лента Мебиуса, описывающая три витка.
Тесно связанным с лентой Мебиуса является загадочный объект - бутылка Клейна. Бутылка Клейна может быть создана склеиванием двух лент Мебиуса друг с другом вдоль их границ. Эта операция не может быть произведена в трехмерном пространстве без создания пересечений внутри фигуры.
Одна из базовых невозможных фигур, невозможный треугольник, может быть представлен как лента Мебиуса, если сгладить некоторые его грани. При этом получится лента Мебиуса, описывающая три витка.
Тесно связанным с лентой Мебиуса является загадочный объект - бутылка Клейна. Бутылка Клейна может быть создана склеиванием двух лент Мебиуса друг с другом вдоль их границ. Эта операция не может быть произведена в трехмерном пространстве без создания пересечений внутри фигуры.
Слайд 4Бутылка Клейна
Бутылка Клейна - это математическая неориентируемая поверхность, в которой неразличимы внутренняя
Бутылка Клейна
Бутылка Клейна - это математическая неориентируемая поверхность, в которой неразличимы внутренняя

и внешняя стороны. Бутылка Клейна впервые была описана в 1882 году немецким математиком Феликсом Клейном. Эта поверхность тесно связана с другой загадочной поверхностью - лентой Мебиуса.
Представим себе бутылку с отверстием в дне. Теперь мысленно удлиним горлышко бутылки, изогнем его в обратном направлении и направим внутрь бутылки сквозь стенку, не касаясь ее (это невозможно произвести в трехмерном пространстве), далее удлиним горлышко до дна бутылки и соединим края горлышка с краями отверстия в дне бутылки. Настоящая бутылка Клейна в четырехмерном пространстве не пересекается сама с собой.
Если рассечь бутылку Клейна на две половинки вдоль плоскости симметрии, то получатся две зеркальных ленты Мебиуса. Фактически, возможно рассечь бутылку Клейна так, что получится одна лента Мебиуса.
Бутылка Клейна может быть создана из одного цилиндра. Один из краев цилиндра загибается в обратную сторону, проходит сквозь цилиндр и склеивается с другим краем. Чтобы совершить это склеивание, необходимо исказить ширину цилиндра. На рисунке ниже показано это преобразование.
Представим себе бутылку с отверстием в дне. Теперь мысленно удлиним горлышко бутылки, изогнем его в обратном направлении и направим внутрь бутылки сквозь стенку, не касаясь ее (это невозможно произвести в трехмерном пространстве), далее удлиним горлышко до дна бутылки и соединим края горлышка с краями отверстия в дне бутылки. Настоящая бутылка Клейна в четырехмерном пространстве не пересекается сама с собой.
Если рассечь бутылку Клейна на две половинки вдоль плоскости симметрии, то получатся две зеркальных ленты Мебиуса. Фактически, возможно рассечь бутылку Клейна так, что получится одна лента Мебиуса.
Бутылка Клейна может быть создана из одного цилиндра. Один из краев цилиндра загибается в обратную сторону, проходит сквозь цилиндр и склеивается с другим краем. Чтобы совершить это склеивание, необходимо исказить ширину цилиндра. На рисунке ниже показано это преобразование.
Слайд 5Невозможный треугольник
В 1934 году Оскар Реутерсвард создал первый невозможный треугольник, составленный из
Невозможный треугольник
В 1934 году Оскар Реутерсвард создал первый невозможный треугольник, составленный из

серии кубиков. Хотя многие художники создавали невозможные фигуры, именно Реутерсвард открыл новый мир фантазий. С тех пор Реутерсвард создал тысячи невозможных фигур. Сегодня он известен как "отец невозможных фигур". В 1980 году Шведское правительство решило разместить невозможный треугольник, а также две другие фигуры Реутерсварда, на почтовых марках, которые выпускались с 1982 года примерно два года.
В 1954 году Роджер Пенроуз после лекции голландского графика М. К. Эшера открыл заново невозможный треугольник и нарисовал его в более привычной форме. В отличие от треугольника Реутерсварда, треугольник Пенроуза нарисован с использованием линейной (а не параллельной, как у Реутерсварда) перспективы, что придает ему больше невозможности. Он опубликовал свой треугольник в 1958 году в Британском журнале психологии в соавторстве со своим отцом Лайонелом Пенроузом .
С этого времени невозможный треугольник появляется несчетное количество раз в различных работах. Благодаря своей популярности многие считают, что невозможный треугольник действительно невозможно воспроизвести в реальном мире, хотя сегодня доказано, что все невозможные фигуры на самом деле возможны. Только невозможными они выглядят лишь с одной точки обзора, а со всех других - обычной фигурой.Наиболее масштабная конструкция невозможного треугольника возведена в австралийском городе Перт в виде 13-метровой скульптуры из алюминия.
В 1954 году Роджер Пенроуз после лекции голландского графика М. К. Эшера открыл заново невозможный треугольник и нарисовал его в более привычной форме. В отличие от треугольника Реутерсварда, треугольник Пенроуза нарисован с использованием линейной (а не параллельной, как у Реутерсварда) перспективы, что придает ему больше невозможности. Он опубликовал свой треугольник в 1958 году в Британском журнале психологии в соавторстве со своим отцом Лайонелом Пенроузом .
С этого времени невозможный треугольник появляется несчетное количество раз в различных работах. Благодаря своей популярности многие считают, что невозможный треугольник действительно невозможно воспроизвести в реальном мире, хотя сегодня доказано, что все невозможные фигуры на самом деле возможны. Только невозможными они выглядят лишь с одной точки обзора, а со всех других - обычной фигурой.Наиболее масштабная конструкция невозможного треугольника возведена в австралийском городе Перт в виде 13-метровой скульптуры из алюминия.
Слайд 6Невозможный трезубец
Среди всех невозможных фигур особое место занимает невозможный трезубец.
Если закрыть рукой
Невозможный трезубец
Среди всех невозможных фигур особое место занимает невозможный трезубец.
Если закрыть рукой

верхнюю часть трезубца, то мы увидим вполне реальную картину - три круглых зуба. Если закрыть нижнюю часть трезубца, то мы тоже увидим реальную картину - два прямоугольных зубца. Но, если рассматривать всю фигуру целиком, то получается что три круглых зубца постепенно превращаются в два прямоугольных.
Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект – плоские грани верхней части трезубца становятся круглыми в нижней.
Никто не знает, кто первым придумал эту фигуру, потому что она появилась практически одновременно в различных изданиях в середине 60-х годов прошлого века. Наиболее известная иллюстрация Нормана Минго была напечатана на обложке журнала "MAD" в марте 1965 года.
Принцип невозможного трезубца используется во многих невозможных фигурах, например вот здесь.
Таким образом, можно увидеть, что передний и задний планы данного рисунка конфликтуют. То есть, то что было изначально на переднем плане уходит назад, а задний план (средний зуб) вылезает вперед. Кроме смены переднего и заднего планов в данном рисунке присутствует еще один эффект – плоские грани верхней части трезубца становятся круглыми в нижней.
Никто не знает, кто первым придумал эту фигуру, потому что она появилась практически одновременно в различных изданиях в середине 60-х годов прошлого века. Наиболее известная иллюстрация Нормана Минго была напечатана на обложке журнала "MAD" в марте 1965 года.
Принцип невозможного трезубца используется во многих невозможных фигурах, например вот здесь.
Слайд 7Невозможная лестница
Невозможная лестница - одна из базовых невозможных фигур. Ее еще иногда
Невозможная лестница
Невозможная лестница - одна из базовых невозможных фигур. Ее еще иногда

называют бесконечной лестницей. Если бы кто-то захотел бы подняться или спуститься по ней, то, пройдя совсем немного, он оказался бы в той же самой точке, откуда начал свой путь. Такую прогулку по лестнице можно продолжать до бесконечности, так и не сдвинувшись с начальной точки.
Модель невозможной лестницы разработал английский биолог Лайонел Пенроуз со своим сыном - известным математиком Роджером Пенроузом. Она была первым невозможным объектом, который М. К. Эшер использовал в своем творчестве - в литографии "Восхождение и спуск" , где изображен загадочный монастырь, на крыше которого воссоздана невозможная лестница.
Рассмотрим более подробно невозможную лестницу (см. рис. ниже). Если двигаться по лестнице по часовой стрелке, то мы будем постоянно подниматься, а если будем двигаться против часовой стрелки, то – спускаться. Хотя может показаться, что такая конструкция невозможна в реальном мире, на самом деле (как и многие из невозможных фигур) невозможную лестницу можно представить в виде реальной модели. Секрет здесь кроется в том, что в реальной модели невозможной лестницы должен быть разрыв в районе правого угла (на рисунке), которого в данном случае не видно, так как точка обзора выбрана намеренно, чтобы скрыть этот разрыв.
Модель невозможной лестницы разработал английский биолог Лайонел Пенроуз со своим сыном - известным математиком Роджером Пенроузом. Она была первым невозможным объектом, который М. К. Эшер использовал в своем творчестве - в литографии "Восхождение и спуск" , где изображен загадочный монастырь, на крыше которого воссоздана невозможная лестница.
Рассмотрим более подробно невозможную лестницу (см. рис. ниже). Если двигаться по лестнице по часовой стрелке, то мы будем постоянно подниматься, а если будем двигаться против часовой стрелки, то – спускаться. Хотя может показаться, что такая конструкция невозможна в реальном мире, на самом деле (как и многие из невозможных фигур) невозможную лестницу можно представить в виде реальной модели. Секрет здесь кроется в том, что в реальной модели невозможной лестницы должен быть разрыв в районе правого угла (на рисунке), которого в данном случае не видно, так как точка обзора выбрана намеренно, чтобы скрыть этот разрыв.
Слайд 8Кольца Борромео
Кольца Борромео - одна из известных невозможных фигур, имеющая древнюю историю.
Кольца Борромео
Кольца Борромео - одна из известных невозможных фигур, имеющая древнюю историю.

Эта фигура основана на симметричной расстановке перекрывающих друг друга колец. Предполагая, что все кольца плоские, такая фигура не может существовать в нашем мире. Для создания фигуры в трехмерном пространстве необходимы разрывы или искажения.
В математике кольца Борромео состоят из трех топологических кругов, объединенных в соединение Брунниана (Brunnian link), таким образом при удалении из конструкции одного из колец мы получаем два разомкнутых кольца.
Во все времена кольца Борромео служили символом "силы в единстве".
В математике кольца Борромео состоят из трех топологических кругов, объединенных в соединение Брунниана (Brunnian link), таким образом при удалении из конструкции одного из колец мы получаем два разомкнутых кольца.
Во все времена кольца Борромео служили символом "силы в единстве".
 Моя первая презентация
Моя первая презентация Управление материальными потоками в производственной логистике АПК
Управление материальными потоками в производственной логистике АПК Крестовые походы
Крестовые походы Компетенции учащихся и навыки, обеспечивающие безопасное участие в дорожном движении
Компетенции учащихся и навыки, обеспечивающие безопасное участие в дорожном движении Виды повреждений организма человека
Виды повреждений организма человека Презентация 1 КН
Презентация 1 КН ЛЕЧЕНИЕ ЗАБОЛЕВАНИЙ С ИСПОЛЬЗОВАНИЕМ УСТРОЙСТВА НА ОСНОВЕ МАТЕРИАЛА С УПРАВЛЯЕМОЙ ЭНЕРГЕТИЧЕСКОЙ СТРУКТУРОЙ CEM Tесн
ЛЕЧЕНИЕ ЗАБОЛЕВАНИЙ С ИСПОЛЬЗОВАНИЕМ УСТРОЙСТВА НА ОСНОВЕ МАТЕРИАЛА С УПРАВЛЯЕМОЙ ЭНЕРГЕТИЧЕСКОЙ СТРУКТУРОЙ CEM Tесн Для начала работы с документ камерой нужно навести мышь на левый нижний угол (кнопка ПУСК) и нажать левую кнопку мыши.
Для начала работы с документ камерой нужно навести мышь на левый нижний угол (кнопка ПУСК) и нажать левую кнопку мыши. Генеральная уборка горничной в номерах
Генеральная уборка горничной в номерах Cannes Festival
Cannes Festival Классификация сталей
Классификация сталей Презентация на тему Экологические факторы среды
Презентация на тему Экологические факторы среды 9 февраля 2011
9 февраля 2011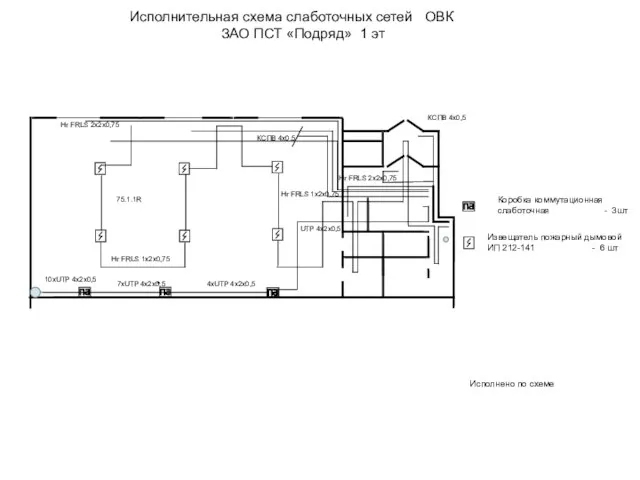 Исполнительная схема слаботочных сетей ОВК. ЗАО ПСТ Подряд 1 этаж
Исполнительная схема слаботочных сетей ОВК. ЗАО ПСТ Подряд 1 этаж Иван Грозный
Иван Грозный Живая вода (9 класс)
Живая вода (9 класс) Моя тренировка на свежем воздухе
Моя тренировка на свежем воздухе В мире призм
В мире призм «Федеральные государственные стандарты основного общего образования: от теории к практике»
«Федеральные государственные стандарты основного общего образования: от теории к практике» Опасные природные явления
Опасные природные явления Что не так с моим кодом или 7 причин моих страданий
Что не так с моим кодом или 7 причин моих страданий Возможности и ограничения применения общенаучных методов познания в методических системах предметного обучения
Возможности и ограничения применения общенаучных методов познания в методических системах предметного обучения Ivanov_Sergey_Alexeevich
Ivanov_Sergey_Alexeevich Дошкольное образование в Германии
Дошкольное образование в Германии Выразительные возможности графических материалов. Изобразительное искусство
Выразительные возможности графических материалов. Изобразительное искусство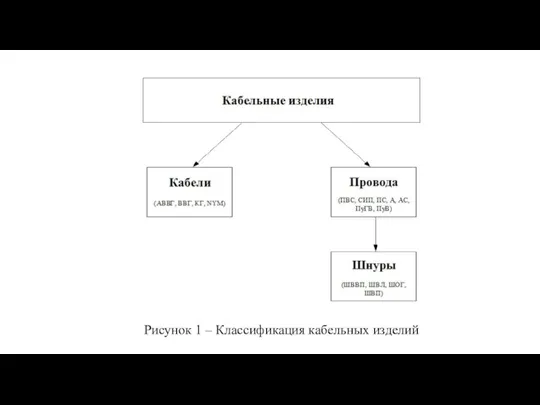 Кабельная продукция
Кабельная продукция Русские щи. 5 лет
Русские щи. 5 лет Морфологические нормы
Морфологические нормы