Новые пределы на вероятности непаулевских переходов в ядрах, полученные на данных эксперимента Борексино
Содержание
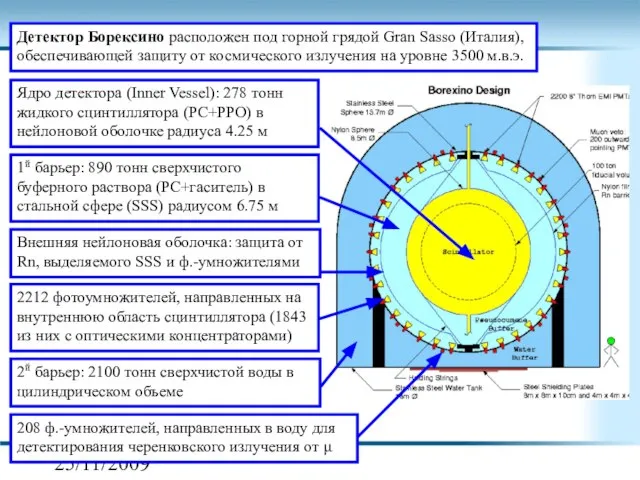
- 2. 25/11/2009 Детектор Борексино расположен под горной грядой Gran Sasso (Италия), обеспечивающей защиту от космического излучения на
- 3. 25/11/2009 Вид детектора изнутри (Inner and Outer Vessels )
- 4. 25/11/2009 Принцип запрета Паули (ПП). "There can never be two or more equivalent electrons in the
- 5. 25/11/2009 Основные эксперименты "В фундаментальной физике, если что-то может быть проверено, оно должно быть проверено." Л.Б.
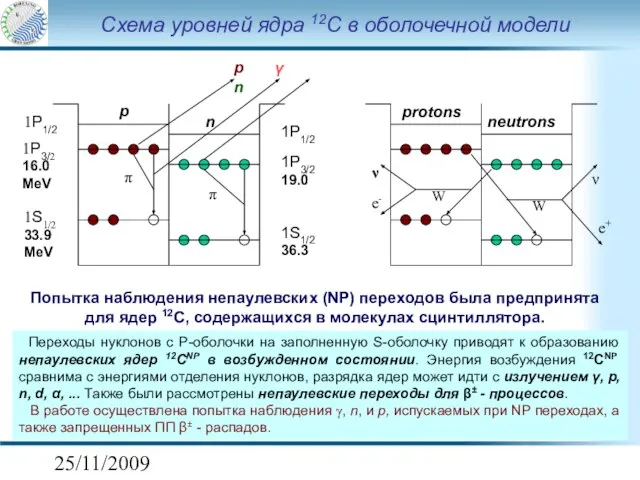
- 6. 25/11/2009 Схема уровней ядра 12C в оболочечной модели 1P1/2 1P3/2 16.0 MeV 1S1/2 33.9 MeV 1P3/2
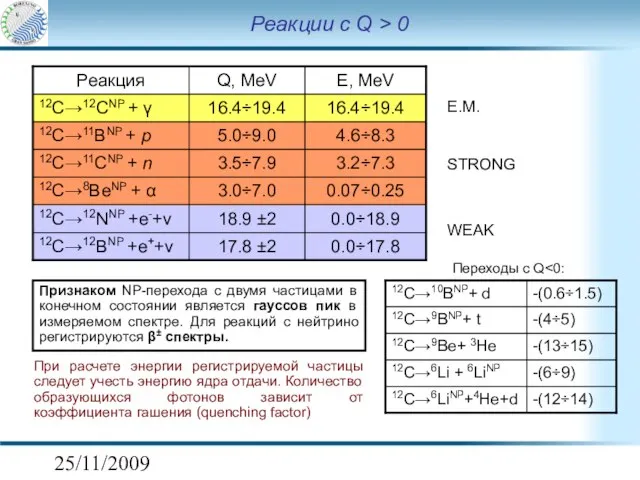
- 7. 25/11/2009 Реакции с Q > 0 При расчете энергии регистрируемой частицы следует учесть энергию ядра отдачи.
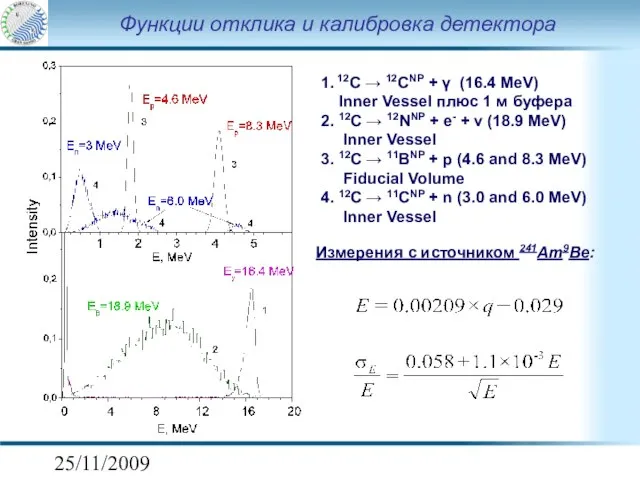
- 8. 25/11/2009 Функции отклика и калибровка детектора 1. 12C → 12CNP + γ (16.4 MeV) Inner Vessel
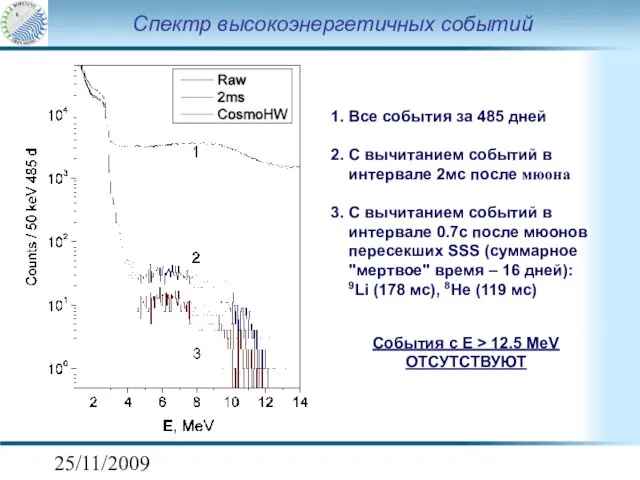
- 9. 25/11/2009 Спектр высокоэнергетичных событий 1. Все события за 485 дней 2. С вычитанием событий в интервале
- 10. 25/11/2009 τ(12C →12CNP + γ) ≥ 5.0 .1031 лет Предел на вероятность перехода 12C→12CNP+γ установлен исходя
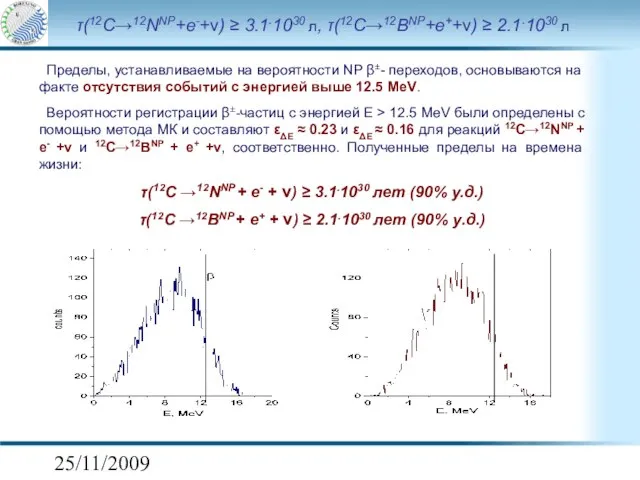
- 11. 25/11/2009 τ(12C→12NNP+e-+ν) ≥ 3.1.1030 л, τ(12C→12BNP+e++ν) ≥ 2.1.1030 л Пределы, устанавливаемые на вероятности NP β±- переходов,
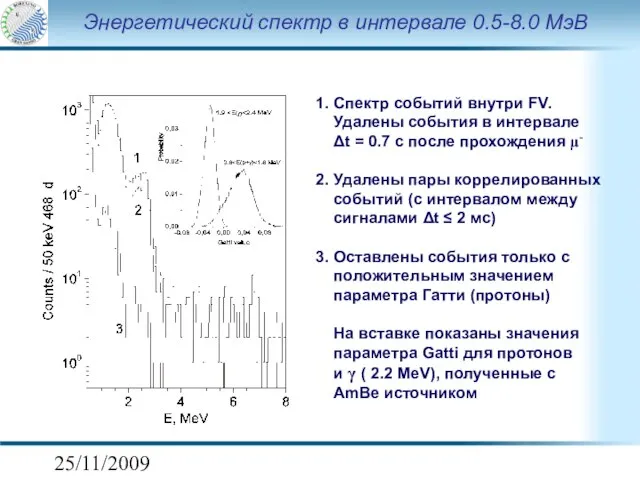
- 12. 25/11/2009 Энергетический спектр в интервале 0.5-8.0 МэВ 1. Спектр событий внутри FV. Удалены события в интервале
- 13. 25/11/2009 τ(12C→11BNP + p) ≥ 2.1.1030 лет • Положение пика: 4.6-8.3 MeV (90% CL), соответствует 1.8-4.1
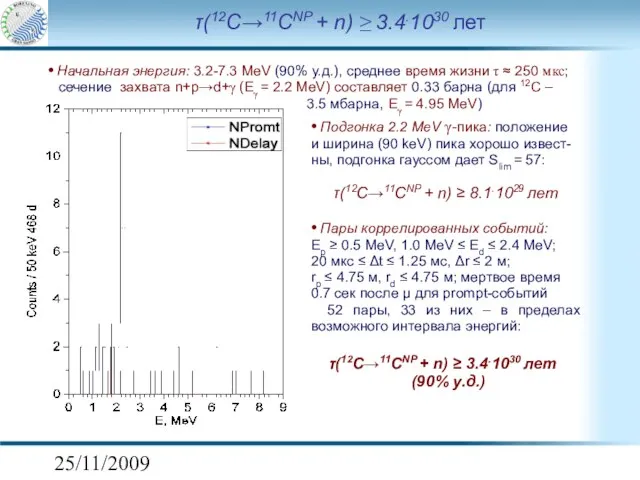
- 14. 25/11/2009 τ(12C→11CNP + n) ≥ 3.4.1030 лет • Начальная энергия: 3.2-7.3 MeV (90% у.д.), среднее время
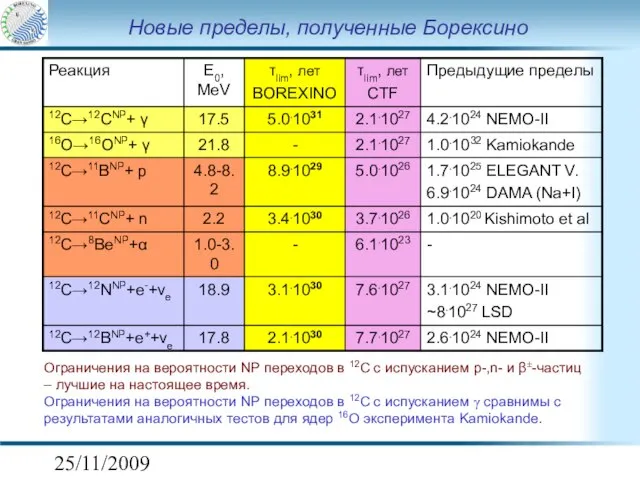
- 15. 25/11/2009 Новые пределы, полученные Борексино Ограничения на вероятности NP переходов в 12C с испусканием p-,n- и
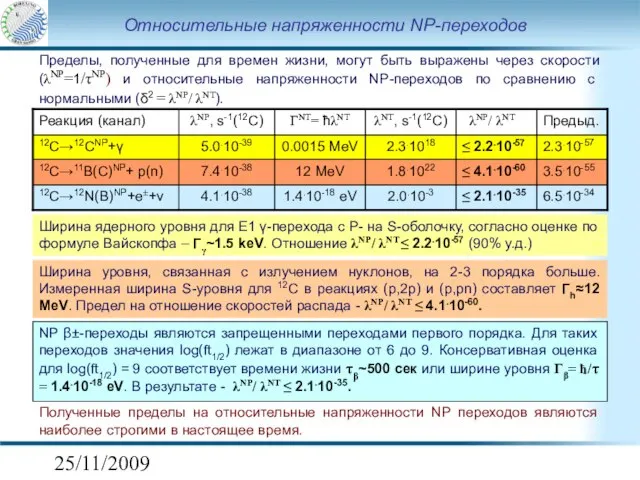
- 16. 25/11/2009 Относительные напряженности NP-переходов Пределы, полученные для времен жизни, могут быть выражены через скорости (λNP=1/τNP) и
- 17. 25/11/2009 Выводы Уникальные характеристики детектора Борексино – рекордно низкий уровень фона, большая масса сцинтиллятора и низкий
- 18. 25/11/2009 Borexino Collaboration Heidelberg (Germany) Munich (Germany)
- 19. 25/11/2009 Энергетический баланс NP переходов Q реакции есть разница между энергиями связи Eb ядер в конечном
- 21. Скачать презентацию








 Переливание крови
Переливание крови Вербальные и невербальные средства общения
Вербальные и невербальные средства общения 1 мм2
1 мм2 Feelings and emotions
Feelings and emotions Во все века героизм и мужество воинов России, мощь и слава русского оружия были неотъемлемой частью величия Российского государст
Во все века героизм и мужество воинов России, мощь и слава русского оружия были неотъемлемой частью величия Российского государст ЗАО “Актив Успеха” внедряет на предприятии систему менеджмента качества в соответствии со стандартом ISO 9001 (ГОСТ Р ИСО 9001-2001).
ЗАО “Актив Успеха” внедряет на предприятии систему менеджмента качества в соответствии со стандартом ISO 9001 (ГОСТ Р ИСО 9001-2001). Способы воздействия в межличностной коммуникации
Способы воздействия в межличностной коммуникации Псалом 19. Святорусский текст церковнославянской псалтири
Псалом 19. Святорусский текст церковнославянской псалтири Мир художественной культуры
Мир художественной культуры Зарубежная Европа. Обострение межнациональных отношений
Зарубежная Европа. Обострение межнациональных отношений Техника продаж для КП, направления II
Техника продаж для КП, направления II Изменения в культуре и быте в первой четверти 18 века
Изменения в культуре и быте в первой четверти 18 века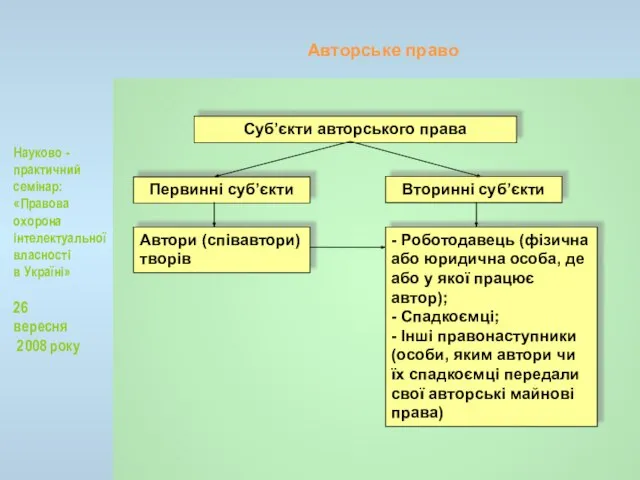 Авторское право
Авторское право Ирландские иллюминированные Евангелия
Ирландские иллюминированные Евангелия Перечень документации, которая должна быть в каждой организации
Перечень документации, которая должна быть в каждой организации Принцип работы NOTAR
Принцип работы NOTAR School of our dreams
School of our dreams Молодежные гранты и стипендии
Молодежные гранты и стипендии  Механизмы психологической защиты и совладания
Механизмы психологической защиты и совладания Music
Music THE GREAT GATSBY 1896 — 1940
THE GREAT GATSBY 1896 — 1940 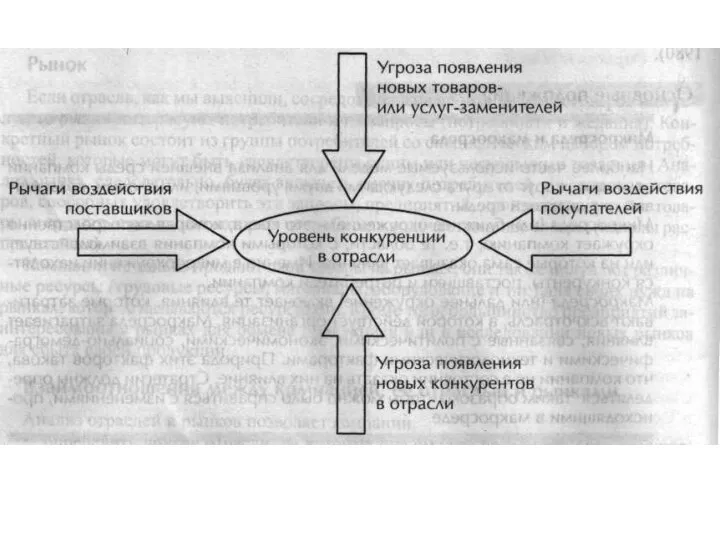 Уровень конкуренции в отрасли
Уровень конкуренции в отрасли Князь Владимир на картинах художников
Князь Владимир на картинах художников Проект постановленияПравительства Омской области «О величине прожиточного минимума на душу населения и по основным социально-
Проект постановленияПравительства Омской области «О величине прожиточного минимума на душу населения и по основным социально- Космос – история и будущее
Космос – история и будущее Использование здоровье сберегающих технологий педагогами в педагогическом процессе ДОУ
Использование здоровье сберегающих технологий педагогами в педагогическом процессе ДОУ Гидравлическая очистка вагонов водой. Модернизация установки
Гидравлическая очистка вагонов водой. Модернизация установки Form and content
Form and content