о математике и математиках

Рене Декарт
В 1637 году вышел в свет главный математический труд Декарта, «Рассуждение о методе» (полное название: «Рассуждение о методе, позволяющем направлять свой разум и отыскивать истину в науках»).
В этой книге излагалась аналитическая геометрия, а в приложениях — многочисленные результаты в алгебре, геометрии, оптике (в том числе — правильная формулировка закона преломления света) и многое другое. Создание аналитической геометрии позволило перевести исследование геометрических свойств кривых и тел на алгебраический язык, то есть анализировать уравнение кривой в некоторой системе координат. Этот перевод имел тот недостаток, что теперь надо было аккуратно определять подлинные геометрические свойства, не зависящие от системы координат (инварианты). Однако достоинства нового метода были исключительно велики, и Декарт продемонстрировал их в той же книге, открыв множество положений, неизвестных древним и современным ему математикам.
В приложении «Геометрия» были даны методы решения алгебраических уравнений (в том числе геометрические и механические), классификация алгебраических кривых. Новый способ задания кривой — с помощью уравнения — был решающим шагом к понятию функции. Декарт формулирует точное «правило знаков» для определения числа положительных корней уравнения, хотя и не доказывает его.
Декарт исследовал алгебраические функции (многочлены), а также ряд «механических» (спирали, циклоида). Для трансцендентных функций, по мнению Декарта, общего метода исследования не существует.
Комплексные числа ещё не рассматривались Декартом на равных правах с положительными, однако он сформулировал (хотя и не доказал) основную теорему алгебры: общее число вещественных и комплексных корней уравнения равно его степени. Отрицательные корни Декарт по традиции именовал ложными, однако объединял их с положительными термином действительные числа, отделяя от мнимых (комплексных). Этот термин вошёл в математику. Впрочем, Декарт проявил некоторую непоследовательность: коэффициенты a, b, c… у него считались положительными, а случай неизвестного знака специально отмечался многоточием слева.

Декарт исследовал алгебраические функции (многочлены), а также ряд «механических» (спирали, циклоида). Для трансцендентных функций, по мнению Декарта, общего метода исследования не существует.
Комплексные числа ещё не рассматривались Декартом на равных правах с положительными, однако он сформулировал (хотя и не доказал) основную теорему алгебры: общее число вещественных и комплексных корней уравнения равно его степени. Отрицательные корни Декарт по традиции именовал ложными, однако объединял их с положительными термином действительные числа, отделяя от мнимых (комплексных). Этот термин вошёл в математику. Впрочем, Декарт проявил некоторую непоследовательность: коэффициенты a, b, c… у него считались положительными, а случай неизвестного знака специально отмечался многоточием слева.
Все неотрицательные вещественные числа, не исключая иррациональные, рассматриваются Декартом как равноправные; они определяются как отношения длины некоторого отрезка к эталону длины. Позже аналогичное определение числа приняли Ньютон и Эйлер. Декарт пока ещё не отделяет алгебру от геометрии, хотя и меняет их приоритеты; решение уравнения он понимает как построение отрезка с длиной, равной корню уравнения. Этот анахронизм был вскоре отброшен его учениками, прежде всего — английскими, для которых геометрические построения — чисто вспомогательный приём.
Книга «Метод» сразу сделала Декарта признанным авторитетом в математике и оптике. Примечательно, что издана она была на французском, а не на латинском языке. Приложение «Геометрия» было, однако, тут же переведено на латинский и неоднократно издавалось отдельно, разрастаясь от комментариев и став настольной книгой европейских учёных. Труды математиков второй половины XVII века отражают сильнейшее влияние Декарта.
Декарт исследовал алгебраические функции (многочлены), а также ряд «механических» (спирали, циклоида). Для трансцендентных функций, по мнению Декарта, общего метода исследования не существует.
Комплексные числа ещё не рассматривались Декартом на равных правах с положительными, однако он сформулировал (хотя и не доказал) основную теорему алгебры: общее число вещественных и комплексных корней уравнения равно его степени. Отрицательные корни Декарт по традиции именовал ложными, однако объединял их с положительными термином действительные числа, отделяя от мнимых (комплексных). Этот термин вошёл в математику. Впрочем, Декарт проявил некоторую непоследовательность: коэффициенты a, b, c… у него считались положительными, а случай неизвестного знака специально отмечался многоточием слева.

Франсуа Виет

Джордж Буль
2 ноября – 195 лет тому назад родился Джордж Буль, или Бул, а также Буул (1815 – 1864), английский математик, основоположник математической логики. В своем произведении "Исследование законов мышления" предпринял попытку построить формальную логику в виде некоторого "исчисления", "алгебры". В современной алгебре мы встречаем так называемые булевы кольца, булевы алгебры – алгебраические системы, законы, композиции которых берут свое начало от исчисления Буля.
Математический анализ
На математические темы Булем в течение жизни были созданы два систематических трактата: «Трактат о дифференциальных уравнениях» (1859; второе издание не завершено, материалы к нему опубликованы посмертно в 1865) и задуманный как его продолжение «Трактат о конечных разностях» (1860). Эти труды внесли важный вклад в соответствующие разделы математики и в то же время продемонстрировали глубокое понимание Булем философии своего предмета.

Математическая логика
Буль был, вероятно, первым после Джона Валлиса математиком, обратившимся к логической проблематике. Идеи применения символического метода к логике впервые высказаны им в статье «Математический анализ логики» (1847). Не удовлетворённый полученными в ней результатами, Буль высказывал пожелание, чтобы о его взглядах судили по обширному трактату «Исследование законов мышления, на которых основываются математические теории логики и вероятностей» (1854). Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов. Единицей Буль обозначал универсум мыслимых объектов, буквенными символами — выборки из него, связанные с обычными прилагательными и существительными (так, если x="рогатые", а y="овцы", последовательный выбор x и y из единицы даст класс рогатых овец). Буль показал, что символика такого рода подчиняется тем же законам, что и алгебраическая, из чего следовало, что их можно складывать, вычитать, умножать и даже делить. В такой символике высказывания могут быть сведены к форме уравнений, а заключение из двух посылок силлогизма — получено путём исключения среднего термина по обычным алгебраическим правилам. Ещё более оригинальной и примечательной была часть его системы, представленной в «Законах мышления…», образующая общий символический метод логического вывода. Буль показал, как из любого числа высказываний, включающих любое число терминов, вывести любое заключение, следующее из этих высказываний, путём чисто символических манипуляций. Вторая часть «Законов мышления…» содержит аналогичную попытку обнаружить общий метод в исчислении вероятностей, позволяющий из заданных вероятностей совокупности событий определить вероятность любого другого события, логически связанного с ними. Профессор Огирко, Игорь на основе теории Буля создал теорию относительности в логике.
Математическая логика
Буль был, вероятно, первым после Джона Валлиса математиком, обратившимся к логической проблематике. Идеи применения символического метода к логике впервые высказаны им в статье «Математический анализ логики» (1847). Не удовлетворённый полученными в ней результатами, Буль высказывал пожелание, чтобы о его взглядах судили по обширному трактату «Исследование законов мышления, на которых основываются математические теории логики и вероятностей» (1854). Буль не считал логику разделом математики, но находил глубокую аналогию между символическим методом алгебры и символическим методом представления логических форм и силлогизмов. Единицей Буль обозначал универсум мыслимых объектов, буквенными символами — выборки из него, связанные с обычными прилагательными и существительными (так, если x="рогатые", а y="овцы", последовательный выбор x и y из единицы даст класс рогатых овец). Буль показал, что символика такого рода подчиняется тем же законам, что и алгебраическая, из чего следовало, что их можно складывать, вычитать, умножать и даже делить. В такой символике высказывания могут быть сведены к форме уравнений, а заключение из двух посылок силлогизма — получено путём исключения среднего термина по обычным алгебраическим правилам. Ещё более оригинальной и примечательной была часть его системы, представленной в «Законах мышления…», образующая общий символический метод логического вывода. Буль показал, как из любого числа высказываний, включающих любое число терминов, вывести любое заключение, следующее из этих высказываний, путём чисто символических манипуляций. Вторая часть «Законов мышления…» содержит аналогичную попытку обнаружить общий метод в исчислении вероятностей, позволяющий из заданных вероятностей совокупности событий определить вероятность любого другого события, логически связанного с ними. Профессор Огирко, Игорь на основе теории Буля создал теорию относительности в логике.

Пафнутий Львович Чебышев
Чебышев считается одним из основоположников теории приближения функций. Работы также в теории чисел, теории вероятностей, механике.
Учёная деятельность Чебышева, начавшаяся в 1843 году появлением в свет небольшой заметки «Note sur une classe d’intégrales définies multiples» («Journ. de Liouville», т. VIII), не прекращалась до конца его жизни. Последний его мемуар «О суммах, зависящих от положительных значений какой-либо функции», вышел в свет уже после его кончины (1895, «Mem. de l’Ас. des sc. de St.-Peters.»).
Из многочисленных открытий Чебышева надо упомянуть прежде всего работы по теории чисел. Начало их положено в прибавлениях к докторской диссертации Чебышева: «Теория сравнений», напечатанной в 1849 году. В 1850 году появился знаменитый «Mémoire sur les nombres premiers», где даны асимптотические оценки для суммы ряда по всем простым числам p.
В 1867 году во II томе «Московского Математического Сборника» появился другой весьма замечательный мемуар Чебышева «О средних величинах», в котором дана теорема, лежащая в основе различных вопросов теории вероятностей и заключающая в себе знаменитую теорему Якова Бернулли как частный случай.
Этих двух работ было бы достаточно, чтобы увековечить имя Чебышева. По интегральному исчислению особенно замечателен мемуар 1860 года, в котором для заданного многочлена x4 + αx3 + βx2 + γx + δ с рациональными коэффициентами даётся алгоритм определения такого числа A, что выражение
интегрировалось в логарифмах, и вычисления соответствующего интеграла.

Одним из любимых приёмов Чебышёва, которым он особенно часто пользовался, было приложение свойств алгебраических непрерывных дробей к различным вопросам анализа.
К работам последнего периода деятельности Чебышева относятся исследования «О предельных значениях интегралов» («Sur les valeurs limites des intégrales», 1873). Совершенно новые вопросы, поставленные здесь Чебышевым, разрабатывались затем его учениками. Последний мемуар Чебышева 1895 года относится к той же области.
Общественная деятельность Чебышева не исчерпывалась его профессурой и участием в делах Академии наук. В качестве члена Ученого комитета Министерства просвещения он рецензировал учебники, составлял программы и инструкции для начальных и средних школ. Он был одним из организаторов Московского математического общества и первого в России математического журнала — «Математический сборник».
В течение сорока лет Чебышев принимал активное участие в работе военного артиллерийского ведомства и работал над усовершенствованием дальнобойности и точности артиллерийской стрельбы. В курсах баллистики до наших дней сохранилась формула Чебышева для вычисления дальности полета снаряда. Своими трудами Чебышев оказал большое влияние на развитие русской артиллерийской науки.
Наиболее оригинальными, как по сущности вопроса, так и по методу решения, являются работы Чебышева «О функциях, наименее уклоняющихся от нуля». Важнейший из этих мемуаров — мемуар 1857 года под заглавием «Sur les questions de minima qui se rattachent à la représentation approximative des fonctions» (в «Мем. Акад. Наук»). Профессор Клейн в своих лекциях, прочитанных в Гёттингенском университете в 1901 году, называл этот мемуар «удивительным» (wunderbar). Его содержание вошло в классическое сочинение I. Bertrand Traité du Calcul diff. et integral. В связи с этими же вопросами находится и работа Чебышева «О черчении географических карт». Этот цикл работ считается основанием теории приближений. В связи с вопросами «о функциях, наименее уклоняющихся от нуля», находятся и работы Чебышева по практической механике, которой он занимался много и с большой любовью.
Также замечательны работы Чебышева об интерполировании, в которых он даёт новые формулы, важные как в теоретическом, так и практическом отношениях.
Одним из любимых приёмов Чебышёва, которым он особенно часто пользовался, было приложение свойств алгебраических непрерывных дробей к различным вопросам анализа.
К работам последнего периода деятельности Чебышева относятся исследования «О предельных значениях интегралов» («Sur les valeurs limites des intégrales», 1873). Совершенно новые вопросы, поставленные здесь Чебышевым, разрабатывались затем его учениками. Последний мемуар Чебышева 1895 года относится к той же области.
Общественная деятельность Чебышева не исчерпывалась его профессурой и участием в делах Академии наук. В качестве члена Ученого комитета Министерства просвещения он рецензировал учебники, составлял программы и инструкции для начальных и средних школ. Он был одним из организаторов Московского математического общества и первого в России математического журнала — «Математический сборник».
В течение сорока лет Чебышев принимал активное участие в работе военного артиллерийского ведомства и работал над усовершенствованием дальнобойности и точности артиллерийской стрельбы. В курсах баллистики до наших дней сохранилась формула Чебышева для вычисления дальности полета снаряда. Своими трудами Чебышев оказал большое влияние на развитие русской артиллерийской науки.

Блез Паскаль (1623-1662)
Французский математик, физик, философ, писатель. Родился в семье юриста, занимающегося математикой. Рано проявил математические способности. Имеет трактат "Опыт о конических сечениях". Сконструировал суммирующую машину. Имеет работы по теории чисел, арифметике, теории вероятностей. Нашёл общий алгоритм для нахождения признаков делимости чисел. Имеет трактат об «Арифметическом треугольнике».

Софья Васильевна Ковалевская
(1850-1891)
Софья Васильевна Ковалевская
(1850-1891)
Для оклейки комнат не хватило обоев, и стены комнаты оклеили листами литографированных лекций М. В. Остроградского по математическому анализу. Впоследствии она стала первой женщиной – математиком, доктором философии. Ей принадлежит роман «Нигилистка».
Научная деятельность
Наиболее важные исследования относятся к теории вращения твёрдого тела. Ковалевская открыла третий классический случай разрешимости задачи о вращении твёрдого тела вокруг неподвижной точки. Этим продвинула вперёд решение задачи, начатое Леонардом Эйлером и Ж. Л. Лагранжем.
Доказала существование аналитического (голоморфного) решения задачи Коши для систем дифференциальных уравнений с частными производными, исследовала задачу Лапласа о равновесии кольца Сатурна, получила второе приближение.
Решила задачу о приведении некоторого класса абелевых интегралов третьего ранга к эллиптическим интегралам. Работала также в области теории потенциала, математической физики, небесной механики.
В 1889 получила большую премию Парижской академии за исследование о вращении тяжёлого несимметричного волчка.

ЭТО ИНТЕРЕСНО
Какой знак вместо плюса используют ученики израильских школ?
Религиозные евреи стараются избегать христианской символики и вообще знаков, похожих на крест. Например, ученики некоторых израильских школ вместо знака «плюс» пишут знак, повторяющий перевёрнутую букву «т».
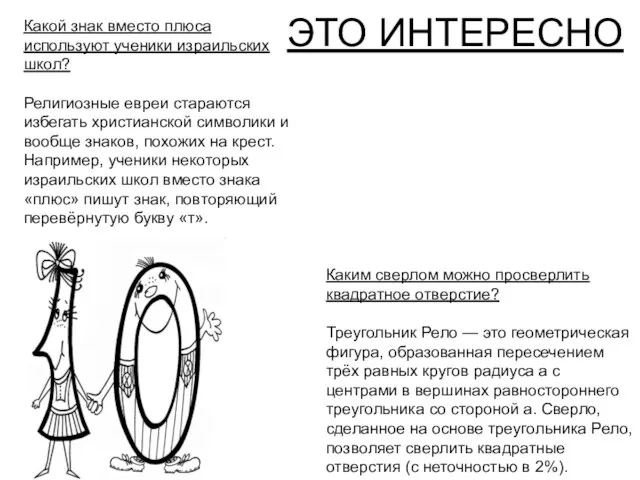
Каким сверлом можно просверлить квадратное отверстие?
Треугольник Рело — это геометрическая фигура, образованная пересечением трёх равных кругов радиуса a с центрами в вершинах равностороннего треугольника со стороной a. Сверло, сделанное на основе треугольника Рело, позволяет сверлить квадратные отверстия (с неточностью в 2%).

Английский математик Абрахам де Муавр в престарелом возрасте однажды обнаружил, что продолжительность его сна растёт на 15 минут в день. Составив арифметическую прогрессию, он определил дату, когда она достигла бы 24 часов — 27 ноября 1754 года. В этот день он и умер.

Чем русское число ноль отличается от западного?
В русской математической литературе ноль не является натуральным числом, а в западной, наоборот, принадлежит ко множеству натуральных чисел.
Чем русское число ноль отличается от западного?
В русской математической литературе ноль не является натуральным числом, а в западной, наоборот, принадлежит ко множеству натуральных чисел.
Когда празднуют день числа Пи?
У числа Пи есть два неофициальных праздника. Первый — 14 марта, потому что этот день в Америке записывается как 3.14. Второй — 22 июля, которое в европейском формате записывается 22/7, а значение такой дроби является достаточно популярным приближённым значением числа Пи.
Кто решил сложную математическую проблему, приняв её за домашнее задание?
Американский математик Джордж Данциг, будучи аспирантом университета, однажды опоздал на урок и принял написанные на доске уравнения за домашнее задание. Оно показалось ему сложнее обычного, но через несколько дней он смог его выполнить. Оказалось, что он решил две «нерешаемые» проблемы в статистике, над которыми бились многие учёные.

Наклонная
Наклонная
Подобие
Теорема Пифагора

Отрезок
Отрезок
Задача

Как записать число 100 шестью цифрами?
99+99/99
Из гнезда вылетели три ласточки. Какова вероятность того, что через 15 секунд они будут находиться в одной плоскости?
100%, три точки всегда образуют одну плоскость
Разделить 5 яблок между пятью лицами так, чтобы каждый получил по яблоку и одно яблоко осталось в корзине.
Один человек берет яблоко вместе с корзиной
Игорь идет к лесному озеру. Ему навстречу движется класс из 25 учеников и два преподавателя. Родители 10 детей также принимают участие в прогулке. Пять матерей еще везут своих детей на колясках. Преподаватель ведет с собой собаку, а двое детей ведут двух крыс.Сколько ног идут по дороге к лесному озеру?
По дороге к лесному озеру идут только две ноги, ноги Игоря. Все, кого он встретил, возвращаются с озера