О ПЛАНЕТАРНЫХ ВОЛНАХ В СИСТЕМЕ ОКЕАН - ЛЕДЯНАЯ ОБОЛОЧКА СПУТНИКА ЮПИТЕРА ЕВРОПА

Планетарные волны
Данные наблюдений миссии Галилео говорят о возможности существования планетарных волн (ротационных и упругих мод в океане спутника Юпитера Европа. Для анализа динамики соответствующих волновых процессов используются две модели.
Первая из них – это вращающийся океан с геометрической стратификацией его ледяной поверхности на отдельные ячейки с характерным размером порядка 100 км. Возможность появления таких ячеек, имеющих гидротермальную природу, содержащих «жидкие линзы», была постулирована и теоретически исследована в 2001 г. Р. Томсоном и Дж. Делане.

Ледяной покров океана
Ледяной покров океана моделируется пологой упругой оболочкой. В этой модели с помощью метода Бубнова – Галеркина найден спектр собственных колебаний жидкости в ячейках Томсона – Делане, соответствующих упруго-гироскопическим планетарным волнам. В целях исследования возможности резонансного возбуждения приливных колебаний жидкости в ячейках доминантные элементы этого спектра сравниваются с теоретическими значениями частот приливообразующих сил, связанных с эксцентриситетом орбиты Европы и возмущениями от других галилевых спутников Юпитера. Это позволяет обнаружить большое количество резонансов на доминантных модах с периодом от 3.5 до 7 суток в областях океана Европы, соответствующих широтам от 30° до 70°.

Океан в целом с ледяной оболочкой
Вторая модель – это невращающийся океан с ледяным покровом, моделируемым моментной упругой сферической оболочкой с массой, отличной от нуля. Дается постановка краевой задачи для гидроупругих планетарных волн, описываемых этой моделью, и приводится точное аналитическое решение краевой задачи в полиномах Лежандра. В полученном спектре собственных колебаний системы оболочка – жидкость обнаруживаются элементы с периодами, близкими к 10 ч. Это создает потенциальную возможность возбуждения соответствующих гидроупругих волн за счет магнитогидродинамических эффектов, связанных с нестационарным магнитным полем Европы, изменяющимся с периодом собственного вращения Юпитера, равным 10 ч.

ВВЕДЕНИЕ
Миссии NASA
Галилео и Кассини
и галилеевы спутники Юпитера

Орбиты КА
Галилео и Кассини

Сближения КА Галилео с Юпитером и его галилеевыми спутниками

Орбиты галилеевых спутников
Ио
Европа
Ганимед
Каллисто

Таблица 1
Периоды обращения
галилеевых спутников в сутках

Европа и ее ледяной покров

Океан Европы

Часть I
Планетарные гироскопические волны в ячейках Томсона - Делане
Б.И. Рабинович (ИКИ)

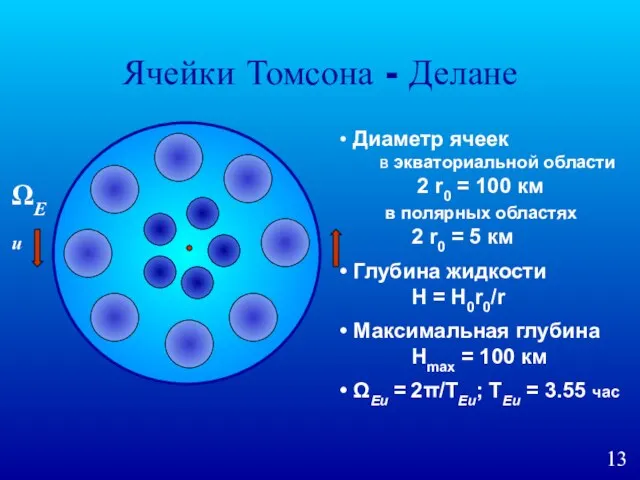
Ячейки Томсона - Делане
ΩEu
Диаметр ячеек
в экваториальной области
2 r0 = 100 км
в полярных областях
2 r0 = 5 км
Глубина жидкости
H = H0r0/r
Максимальная глубина
Hmax = 100 км
ΩEu = 2π/TEu; TEu = 3.55 час

Краевая задача

Условные обозначения (1)
v – скорость жидкости;
H – толщина слоя жидкости;
γ/g – массовая плотность жидкости;
P* – вариация давления на жидкость со стороны упругой ледяной оболочки;
w – перемещение элемента жидкости в направлении нормали к картинной плоскости;
С – контур области S, занятой жидкостью;
vν – компонент скорости в проекции на нормаль контуру C (орт внешней нормали ν);

Условные обозначения (2)
∇, Δ – двумерные операторы Гамильтона и Лапласа;
L и L0 – дифференциальные операторы теории пологих оболочек;
j – ускорение гравитационной силы на поверхности Европы;
f – параметр Кориолиса, f = 2 Ω sinϕ;
Ω - угловая скорость собственного вращения Европы: Ω = 2π/T;
T – период ее собственного вращения, равный периоду обращения вокруг Юпитера;
ϕ - широта точки области S.

Функция тока

Метод Бубнова - Галеркина

Частоты собственных колебаний жидкости

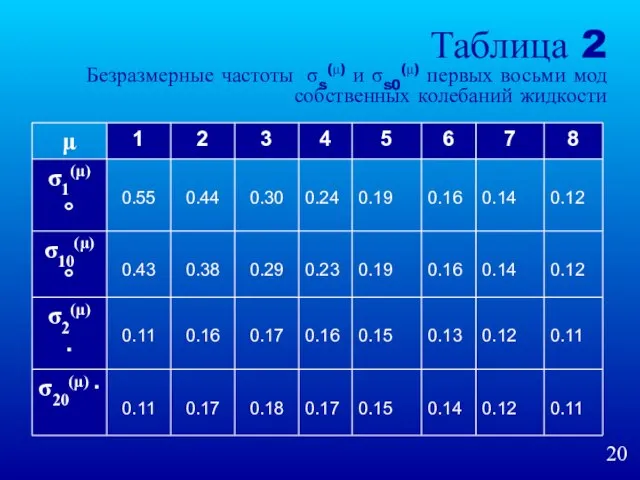
Таблица 2
Безразмерные частоты σs(μ) и σs0(μ) первых восьми мод собственных колебаний жидкости

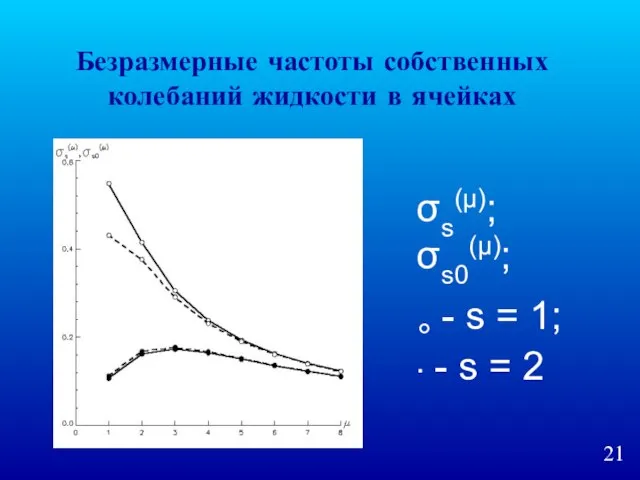
Безразмерные частоты собственных колебаний жидкости в ячейках
σs(μ); σs0(μ);
° - s = 1;
∙ - s = 2

Резонансное возбуждение приливных колебаний жидкости

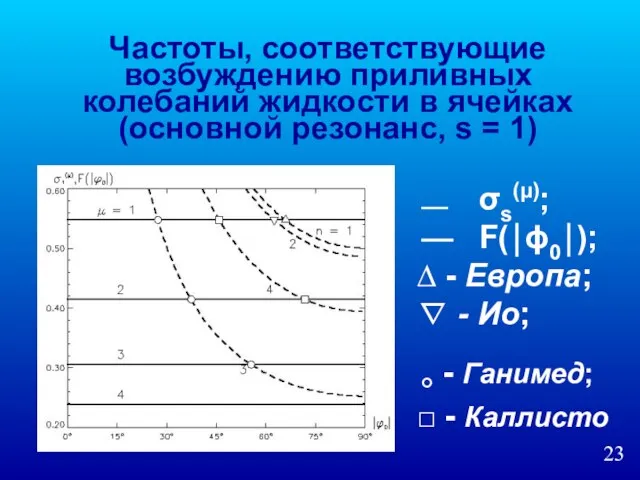
Частоты, соответствующие возбуждению приливных колебаний жидкости в ячейках
(основной резонанс, s = 1)
σs(μ);
F(⏐ϕ0⏐);
∆ - Европа;
∇ - Ио;
° - Ганимед;
□ - Каллисто

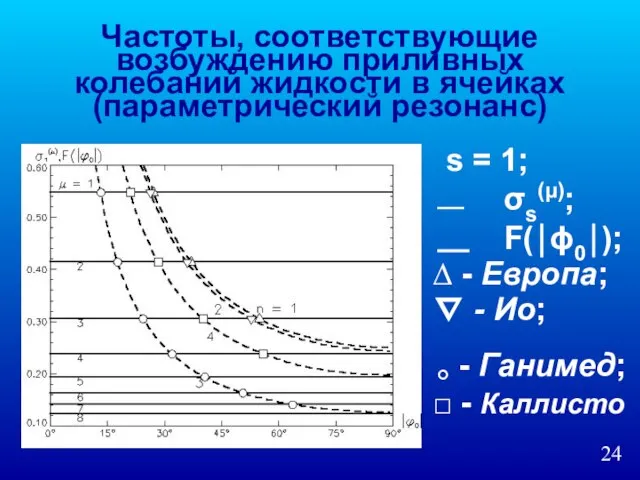
Частоты, соответствующие возбуждению приливных колебаний жидкости в ячейках (параметрический резонанс)
s = 1;
σs(μ);
F(⏐ϕ0⏐);
∆ - Европа;
∇ - Ио;
° - Ганимед;
□ - Каллисто

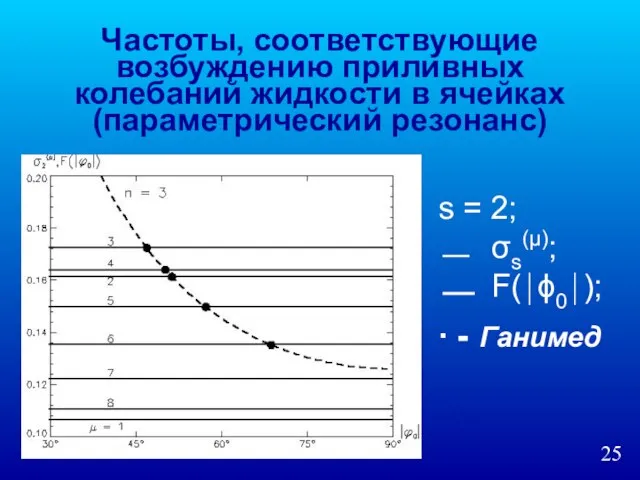
Частоты, соответствующие возбуждению приливных колебаний жидкости в ячейках (параметрический резонанс)
s = 2; σs(μ);
F(⏐ϕ0⏐);
∙ - Ганимед

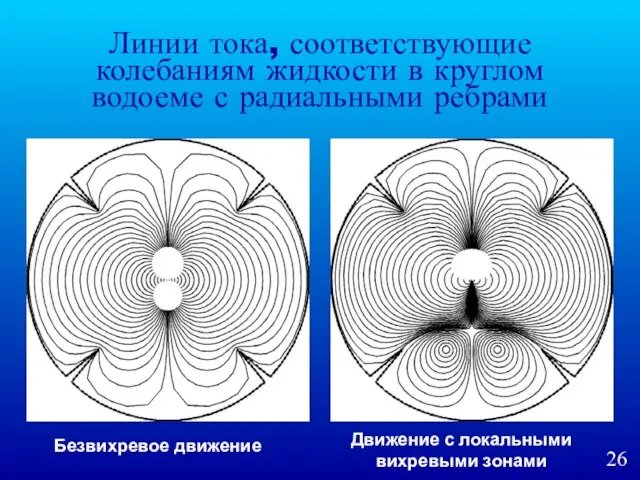
Линии тока, соответствующие колебаниям жидкости в круглом водоеме с радиальными ребрами
Безвихревое движение
Движение с локальными вихревыми зонами

Часть II
Планетарные гидроупругие волны в ледяной оболочке Европы
Л.В. Докучаев (ЦНИИМАШ)

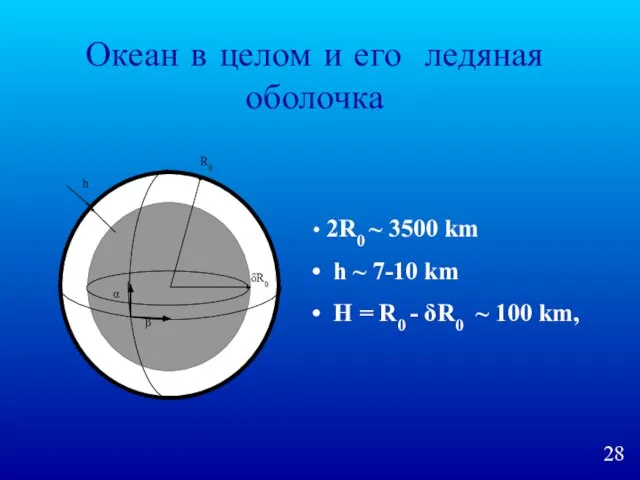
Океан в целом и его ледяная оболочка
2R0 ~ 3500 km h ~ 7-10 km
H = R0 - δR0 ~ 100 km,

Общие уравнения гидродинамики

Уравнения колебаний сферической оболочки

Вспомогательные переменные
u(α,β,t),v(α,β,t) – тангенциальные перемещения,
w(α,β,t) – перемещения по нормали,
α, β - географические широта и долгота

Потенциал смещений Краевая задача и фундаментальные решения

Разложение решений в ряды

Характеристическое уравнение 1

Характеристическое уравнение 2

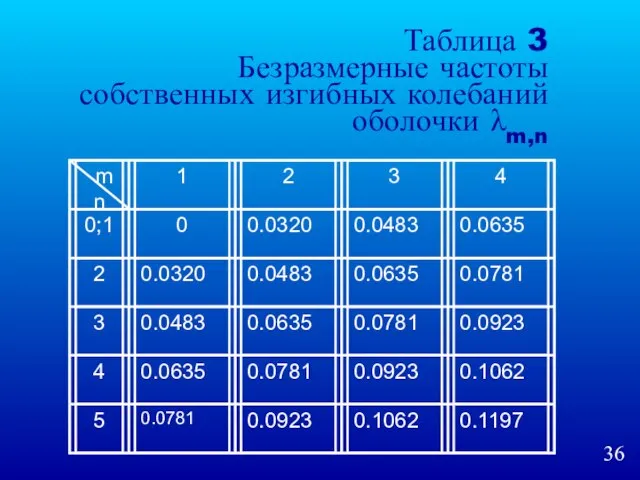
Таблица 3
Безразмерные частоты собственных изгибных колебаний оболочки λm,n

Размерные частоты и периоды
R0 = 1744000 м, h = 7500 м,
ρ = 900 кг/м3, μ = 0.1, Е = 1010 н/м2.
Период изменения магнитного поля Европы = 10 час

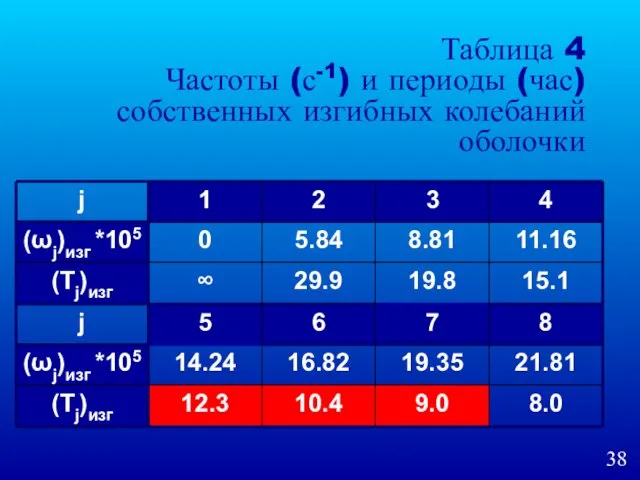
Таблица 4
Частоты (с-1) и периоды (час) собственных изгибных колебаний оболочки