О ВЛИЯНИИ ПРЕЦЕССИИ ОРБИТЫ ЛУНЫ НА ЭВОЛЮЦИЮ И ВРЕМЯ СУЩЕСТВОВАНИЯ ВЫСОКОАПОГЕЙНЫХ ОРБИТ ИСЗ

АННОТАЦИЯ
Проблема выбора орбит ИСЗ с длительным временем существования не является новой. Она всегда была актуальной, однако в последние годы эта проблема приобрела большую актуальность из-за того, что существенно повысился ресурс бортовых приборов и бортовой энергетики. Теперь необходимое время существования орбит измеряется не годами, а десятилетиями. Это заставило произвести переоценку ценностей и вернуться к рассмотрению факторов, влияющих на длительность времени существования.

Введение
Полученное в классической работе М.Л. Лидова [1961] решение для спутникового варианта двукратно- осредненной ограниченной задачи трех тел содержат необходимые, но не достаточные рекомендации для решения рассматриваемой задачи.
Численные эксперименты в рамках ретроспективного анализа времени существования спутников серии «Прогноз», запущенных на высокоапогейные орбиты в 1972 - 1995, показали существенное влияние некоторых факторов, которые лежат вне решения осредненной задачи трех тел

Введение (2)
Для орбиты «Прогноз-6» с начальным значением высоты апогея (перигея) 197 900 км (498 км) и датой старта 22.09.1977 время существования составляло около 40 лет.
Численный расчет эволюции под влиянием гравитационных возмущений от Луны и Солнца для гипотетического варианта орбиты «Прогноз-6» с измененной ровно на один год датой старта (1978) и фиксированными значениями всех остальных начальных условий дает время существования более 500 лет.
А гипотетический перенос запуска на 1988 год привел бы ко времени баллистического существования не более 7 лет.

Введение (3)
Здесь дело в прецессии орбиты Луны (которая, сохраняя постоянное наклонение к плоскости эклиптики около 5.5°, прецессирует с периодом 18.6 года).
Упомянутые орбиты типа ПРОГНОЗ-6 с разными датами старта отличаются начальными значениями углового расстояния между линиями узлов орбиты спутника и орбиты Луны на плоскости эклиптики.
Это различие никак не влияет на процесс эволюции, описываемый решением осредненной задачи.

Введение (4)
Это приводит к необходимости создания инструментов для анализа эволюции орбит с учетом новых факторов.
Использование для этих исследований численных методов решения полной системы дифференциальных уравнений требует очень больших затрат машинного времени на той технике, которой мы располагаем на сегодняшний день.
Расчет эволюции орбиты высокоапогейного спутника с учетом влияния Луны и Солнца на 10 лет требует около 50 мин машинного времени.

Введение (5)
Мы предлагаем алгоритм, основанный на использовании эволюции по Лидову в качестве невозмущенного движения, а прецессию орбиты Луны – в качестве возмущающего фактора.
В докладе обсуждаются различные аспекты разработки этого алгоритма и первые результаты его использования.

Полученные М.Л. Лидовым [1961] аналитические решения двукратно осредненной ограниченной задачи трех тел в хилловском приближении
a - большая полуось, ε = 1 - e2, e – эксцентриситет;
i, ω, и Ω - наклонение, аргумент перицентра и прямое восхождение восходящего узла орбиты ИСЗ, отнесенные к плоскости орбиты возмущающего тела; N – номер витка; ε1 – параметр ε орбиты возмущающего тела; M, M1– масса центрального и возмущающего тел
С1
С2
Область возможных значений интегральных констант с1, с2

Примечание: Здесь приведены выражения для параметров k, ϕ, ατ для c2 > 0 при c2 < 0 в выражениях (5), (6) нужно поменять местами α и β
Зависимость орбитальных элементов от времени τ
β = 1-5/2c2 ; α , γ корни уравнения:
Использование замены переменных
Tu = 2 K(k) - период изменения ε(u) ; Tτ = 2 ατ K(k) - период изменения ε(τ)
В работе Ю.Ф. Гордеевой [1968] получено выражение зависимости эволюции орбитальных элементов от времени через эллиптический интеграл первого рода.
приводит к выражению τ через эллиптический интеграл первого рода
где
где u = τ/ατ
(5)
(6)

Безразмерный период либрационных составляющих эволюции орбитальных элементов
Выразим период либрации T через безразмерный период TC , который в свою очередь выражается через безразмерные параметры
⎟LС(c1, c2)⎜ = 2 ατ K(k);
K (k)- полный эллиптический интеграл первого рода.
a* - большая полуось спутника;
LD - параметр подобия возмущений;
(7)
(8)

Используемые варианты безразмерного времени и соответствующие им значения либрационного периода
t* = t/χ (либрационный период TC)
τ = t* /B (либрационный период ⎟Lc⎜)
u = τ/ατ (либрационный период 2K)
φ = π u/K(k)+ π/2 (либрационный период 2π)

Выражение для Ω в функции параметра τ
Далее возможны два пути :
Использование полученного М.А Вашковьяком [1999] решения, основанного на представлении ε через sn эллиптический, что приводит к выражению Ω (τ) через эллиптические интегралы третьего рода
Использование приближенной апроксимации ε с помощью sin(φ), что позволяет выразить Ω (τ) через элементарные функции

Применение гармонической апроксимации
Табличный интеграл I(φ)
Замена переменной φ = 2π τ/⎟Lc⎜+ π/2
(9)
(10)

Представление Ω в функции параметра φ в виде суммы ротационной и либрационной составляющих
(11)
(12)
(13)
(14)

Период ротационной составляющей эволюции Ω, при аппроксимации синусом
(15)
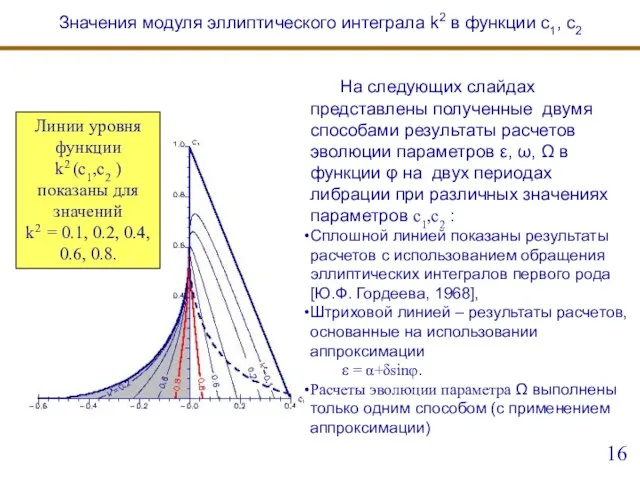
(16)

На следующих слайдах представлены полученные двумя способами результаты расчетов эволюции параметров ε, ω, Ω в функции φ на двух периодах либрации при различных значениях параметров с1,с2 :
Сплошной линией показаны результаты расчетов с использованием обращения эллиптических интегралов первого рода [Ю.Ф. Гордеева, 1968],
Штриховой линией – результаты расчетов, основанные на использовании аппроксимации
ε = α+δsinφ.
Расчеты эволюции параметра Ω выполнены только одним способом (с применением аппроксимации)
Линии уровня функции
k2 (c1,c2 ) показаны для значений
k2 = 0.1, 0.2, 0.4, 0.6, 0.8.
Значения модуля эллиптического интеграла k2 в функции с1, с2

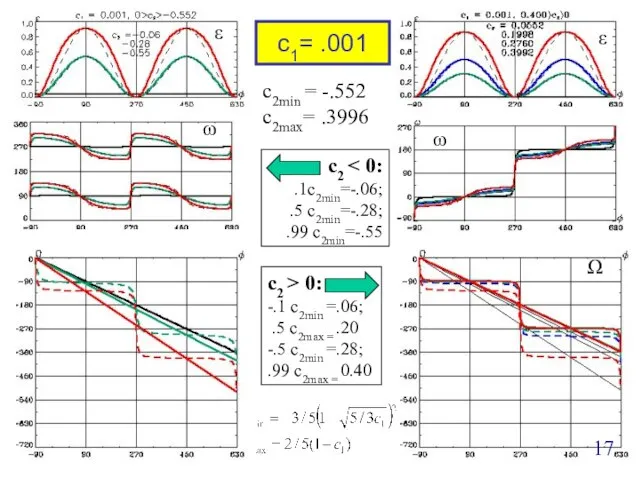
Ω
ε
ω
c1= .001
Ω
ω
ε
c2min = -.552
c2max= .3996
c2 < 0:
.1c2min=-.06;
.5 c2min=-.28;
.99 c2min=-.55
c2 > 0:
-.1 c2min =.06;
.5 c2max = .20
-.5 c2min =.28;
.99 c2max = 0.40

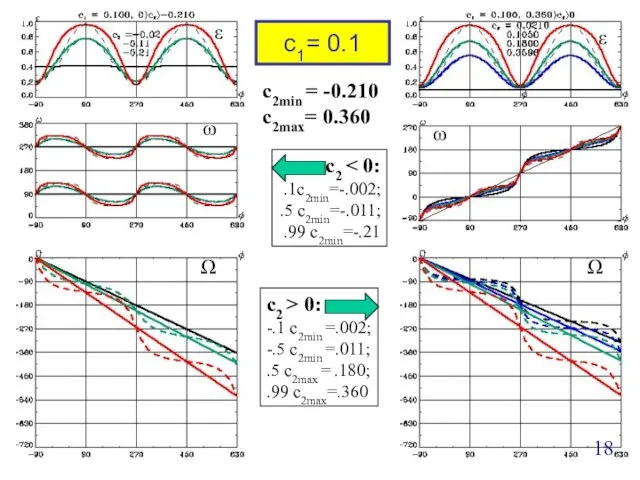
Ω
ε
ω
c1= 0.1
Ω
ω
ε
c2min = -0.210
c2max= 0.360
c2 < 0:
.1c2min=-.002;
.5 c2min=-.011;
.99 c2min=-.21
c2 > 0:
-.1 c2min =.002;
-.5 c2min =.011;
.5 c2max = .180;
.99 c2max=.360

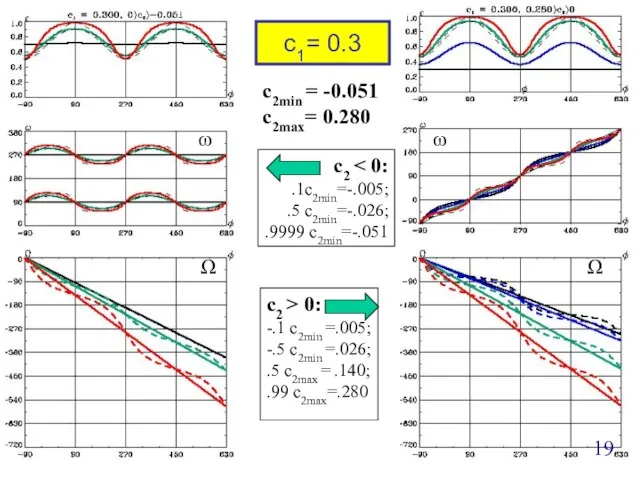
Ω
ε
ω
c1= 0.3
c2 < 0:
.1c2min=-.005;
.5 c2min=-.026;
.9999 c2min=-.051
c2 > 0:
-.1 c2min =.005;
-.5 c2min =.026;
.5 c2max = .140;
.99 c2max=.280
Ω
ω
ε
c2min = -0.051
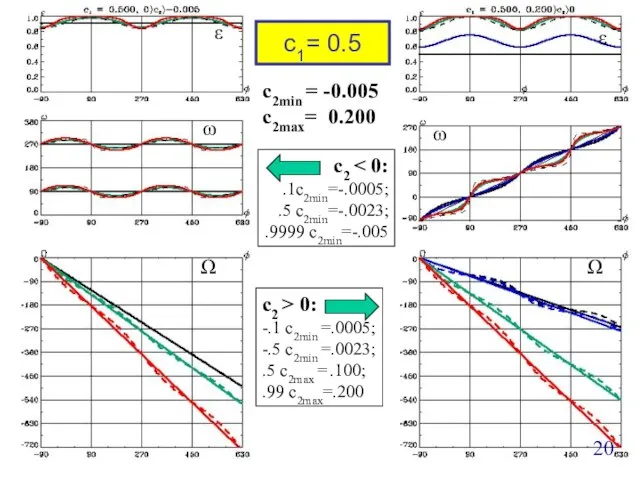
c2max= 0.280

Ω
ε
ω
c1= 0.5
Ω
ω
ε
c2min = -0.005
c2max= 0.200
c2 < 0:
.1c2min=-.0005;
.5 c2min=-.0023;
.9999 c2min=-.005
c2 > 0:
-.1 c2min =.0005;
-.5 c2min =.0023;
.5 c2max = .100;
.99 c2max=.200

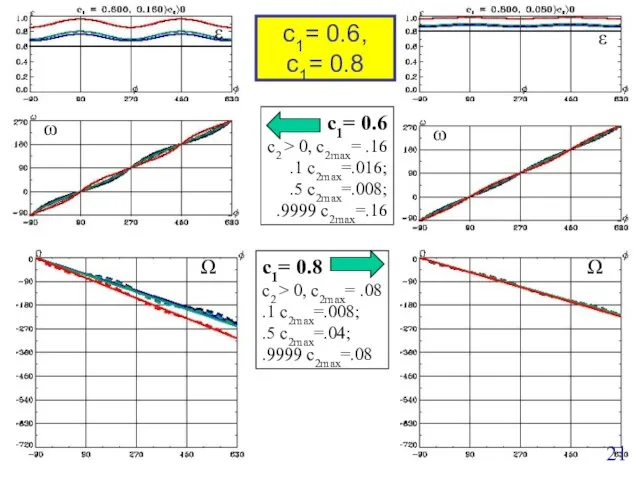
c1= 0.6
c2 > 0, c2max= .16
.1 c2max=.016;
.5 c2max=.008;
.9999 c2max=.16
Ω
ε
ω
c1= 0.6, c1= 0.8
c1= 0.8
c2 > 0, c2max= .08
.1 c2max=.008;
.5 c2max=.04;
.9999 c2max=.08
Ω
ω
ε

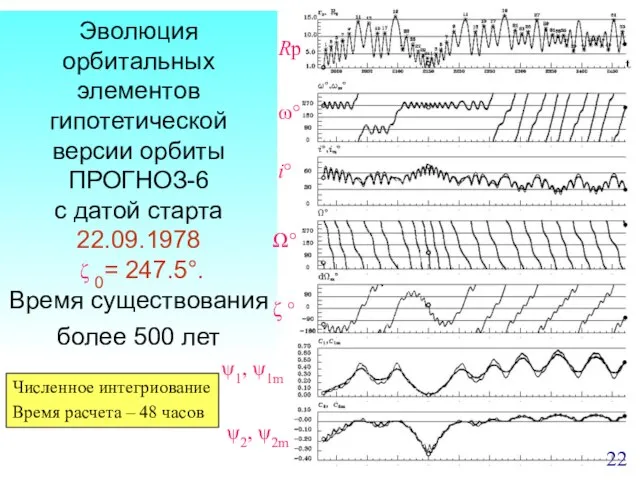
Эволюция орбитальных элементов гипотетической версии орбиты ПРОГНОЗ-6
с датой старта
22.09.1978
ζ 0= 247.5°.
Время существования
более 500 лет
Rp
ω°
i°
Ω°
ζ °
ψ1, ψ1m
ψ2, ψ2m
Численное интегриование
Время расчета – 48 часов

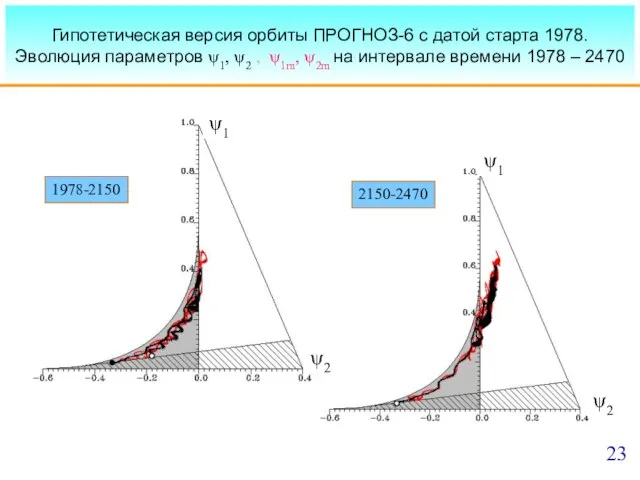
Гипотетическая версия орбиты ПРОГНОЗ-6 с датой старта 1978. Эволюция параметров ψ1, ψ2 , ψ1m, ψ2m на интервале времени 1978 – 2470
1978-2150
2150-2470
ψ1
ψ2
ψ2
ψ1

Полуаналитический метод прогноза эволюции орбит под влиянием гравитационных возмущений внешнего тела с учетом прецессии орбиты возмущающего тела
В качестве основной плоскости отсчета будем использовать плоскость, перпендикулярную к оси прецессии орбиты возмущающего тела и проходящую через центральную точку. В нашей задаче возмущающее тела это Луна, а основная плоскость совпадает с плоскостью эклиптики.
На следующе слайдах представлены тригонометрические формулы используемые для перехода от одной плоскости отсчета к другой.

Связь между угловыми элементами i, ω, отсчитанными относительно плоскости эклиптики, и соответствующими элементами im, ωm, отсчитанными относительно плоскости орбиты Луны
Зависимость значений im, ωm от i, ω и углового расстояния ζ между восходящими узлами орбит спутника и Луны на плоскости эклиптики определяется следующими соотношениями:
cos im = cos ζ sin i sin δ + cos i cos δ; Δi = im - i;
cos Δω = (sin i cos δ - cos ζ cos i sinδ) / sin im;
sin Δω= - sin δ sin ζ / sin im; ωm = ω + Δω
cos ζ m = (sin im cos i - cos Δω cos im sin i)/sin δ;
cos ζ m = (-sin δ cos i + cos ζ cos δ sin i) / sin im;
sin ζ m = sin i sin ϕ / sin im; Δ ζ = ζ m – ζ
где δ = 5.5° - наклонение плоскости орбиты Луны к плоскости эклиптики,
ζ m - угловое расстояние линии узлов орбиты спутника на плоскости орбиты Луны от линии пересечения орбиты Луны с плоскостью эклиптики
(17)
(18)

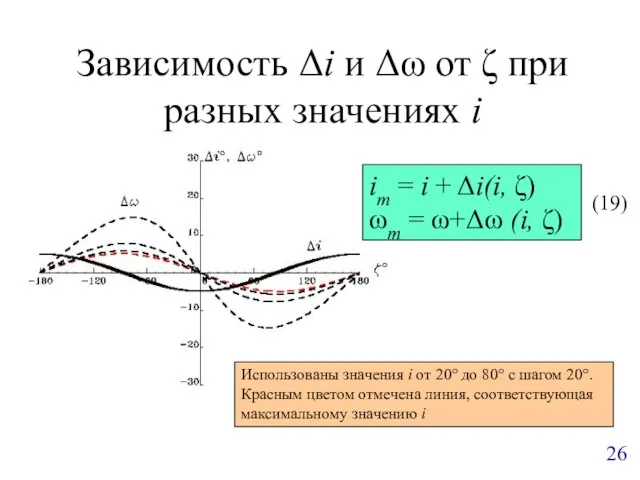
Зависимость Δi и Δω от ζ при разных значениях i
im = i + Δi(i, ζ)
ωm = ω+Δω (i, ζ)
Использованы значения i от 20° до 80° с шагом 20°.
Красным цветом отмечена линия, соответствующая максимальному значению i
(19)

Описание алгоритма (1)
Исходя из начальных условий a0, ε0 , i0, ω0, Ω0, ζ0 = Ω0 - Ω0M , заданных в момент времени t0 относительно плоскости эклиптики, рассчитываем значения ψ10 , ψ20 по формулам, правые части которых совпадают с правыми частями первых интегралов c1 , c2 (4) Лидовского решения осредненной задачи.
Переходим к плоскости орбиты Луны, рассчитываем угловые элементы i0m, ω0m относительно этой плоскости по формулам (17) и значения ψ10m , ψ20m по формулам (4) .

Описание алгоритма (2)
Делаем шаг Δt , используя Лидовское решение (6 - 16) учитывающее в качестве орбита возмущающего тела орбиту Луны замороженную на момент времени t0. Получаем значения ε1 , i1m, ω1m, ζ1m, соответствующие моменту времени t1 = t0 + Δt.
Возвращаемся к плоскости эклиптики, преобразуем угловые элементы по формулам (17), (18), получаем i1, ω1, ζ1 , Ω1 = Ω0M + ζ1 . Первый шаг завершен.
Для нового шага используем орбиту Луны, замороженную на момент времени t1

Сопоставление результатов полуаналитического расчета эволюции орбитальных элементов и результатов численного интегрирования
На следующих слайдах на примере орбиты типа ПРОГНОЗ-6 с гипотетическим стартом в 1978 году приводится сопоставление результатов полуаналитического расчета эволюции орбитальных элементов и результатов численного интегрирования на интервале времени 150 лет.
И в том и в другом расчете учитываются гравитационные возмущений от Луны и Солнца и прецессия орбиты Луны
Для сопоставления используются следующих параметры: три угловых элемента орбиты ω, i, Ω; угловое расстояния ζ между линиями узлов орбиты спутника и орбиты Луны на плоскости эклиптики; параметры ψ1, ψ2, правые части которых соответствуют двум первым интегралам двукратно-осредненной задачи трех тел.
Различие состоит параметре, характеризующем форму орбиты: в первом случае используется параметр ε= 1-e2, а во втором случае – Rp, радиус перицентра (измеряемый в радиусах земли). Эти параметры связаны между собой взаимно однозначным соответствием при известном значении большой полуоси a и имеют аналогичный характер эволюции.

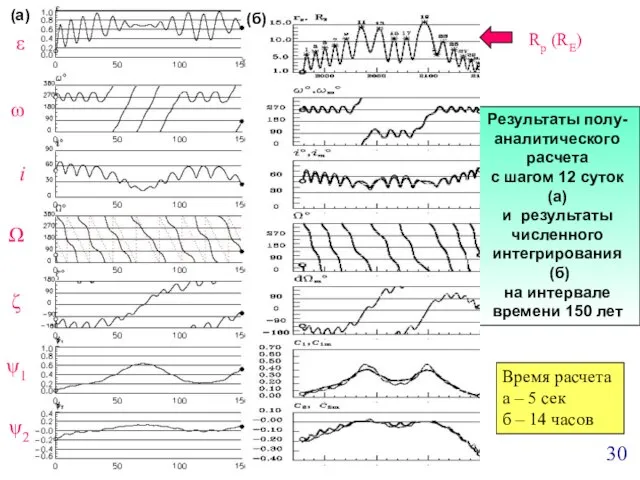
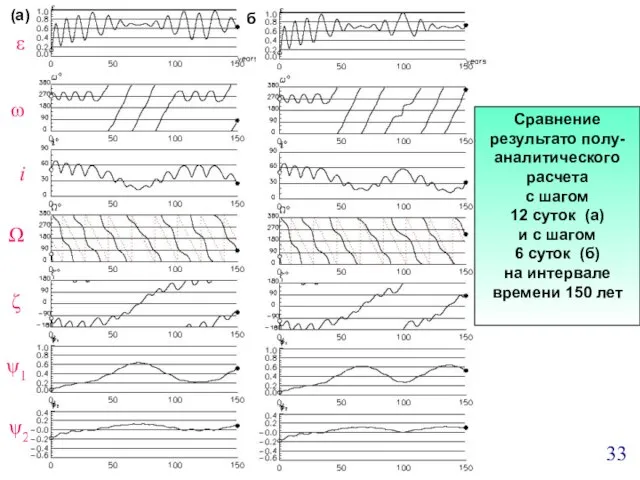
Результаты полу- аналитического расчета
с шагом 12 суток (а)
и результаты численного интегрирования
(б)
на интервале времени 150 лет
ε
ω
Ω
i
ζ
ψ1
ψ2
Rp (RE)
(а)
(б)
Время расчета
а – 5 сек
б – 14 часов

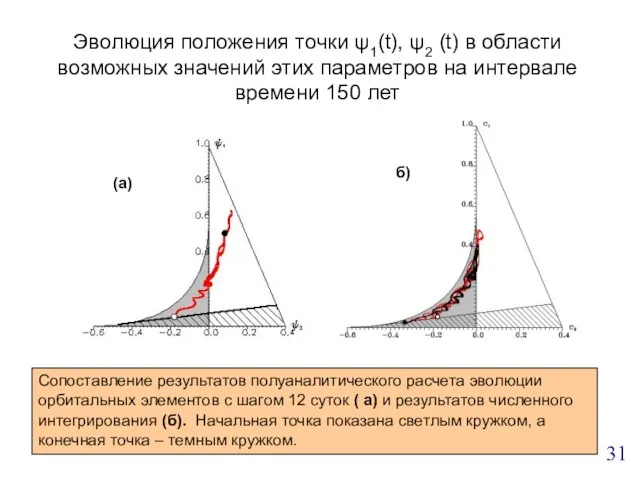
Эволюция положения точки ψ1(t), ψ2 (t) в области возможных значений этих параметров на интервале времени 150 лет
(а)
б)
Сопоставление результатов полуаналитического расчета эволюции орбитальных элементов с шагом 12 суток ( а) и результатов численного интегрирования (б). Начальная точка показана светлым кружком, а конечная точка – темным кружком.

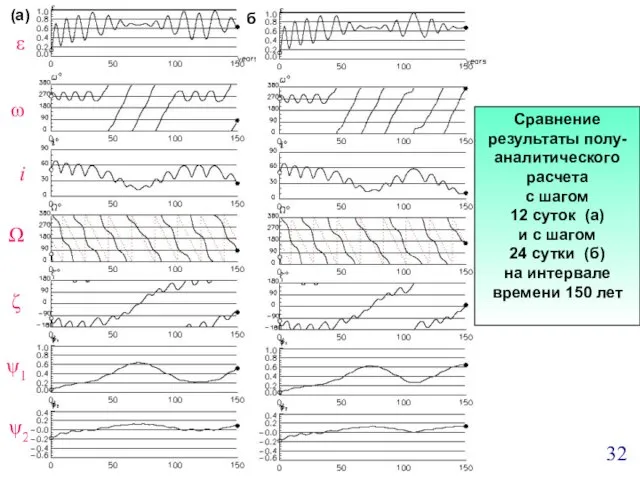
ε
ω
Ω
i
ζ
ψ1
ψ2
б)
(а)
Сравнение результаты полу- аналитического расчета
с шагом
12 суток (а)
и с шагом
24 сутки (б)
на интервале времени 150 лет

ε
ω
Ω
i
ζ
ψ1
ψ2
б)
(а)
Сравнение результато полу- аналитического расчета
с шагом
12 суток (а)
и с шагом
6 суток (б)
на интервале времени 150 лет

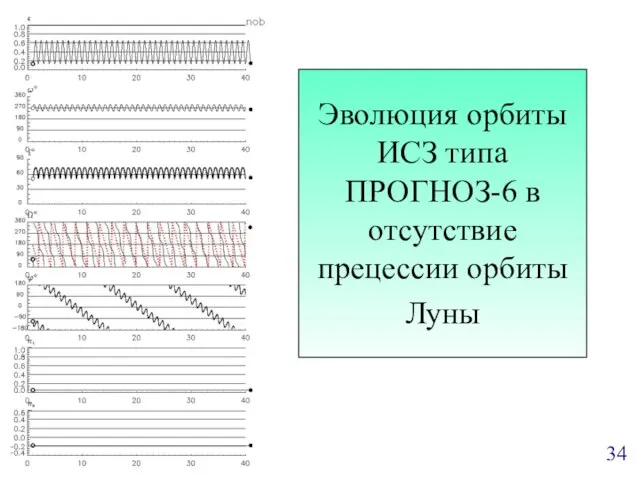
Эволюция орбиты ИСЗ типа ПРОГНОЗ-6 в отсутствие прецессии орбиты Луны

Заключение
Разработан эффективный инструмент исследования эволюции и времени существования орбит ИСЗ подверженных гравитационных возмущений от Луны и Солнца.
Полученный алгоритм отличается очень большим быстродействием. Расчет эволюции орбиты на 150 лет занимает не более 5 секунд против 14 часов при численном интегрировании.
Это открывает широкие возможности для его применения как для выбора орбит, так и для исследования закономерностей эволюции различных классов орбит.