Об одном удивительном математическом парадоксе связанном с обратимыми клеточными автоматами(Наша презентация состоит из двух ч

1. Введение
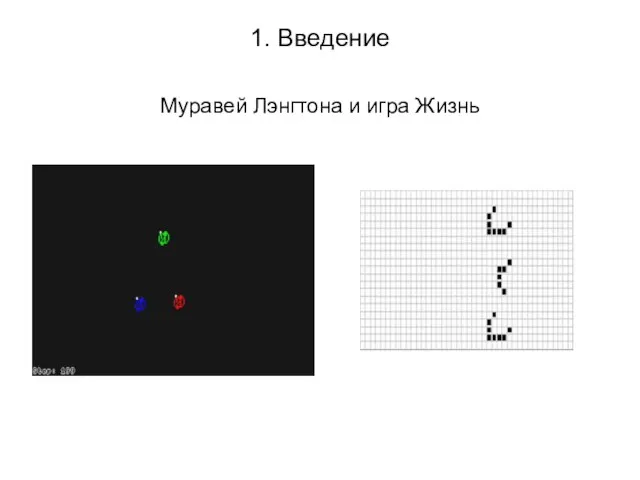
Муравей Лэнгтона и игра Жизнь

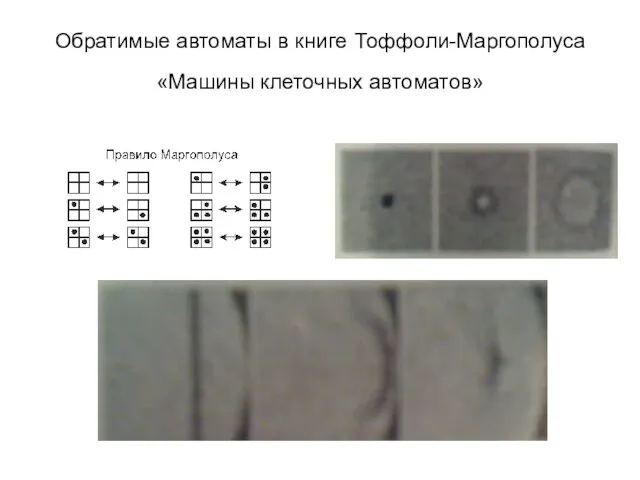
Обратимые автоматы в книге Тоффоли-Маргополуса
«Машины клеточных автоматов»

2. Обратимые клеточные автоматы
Утверждения: 1) Если ОКА начал двигаться, то он
никогда не остановится; 2) При своём движении он
обязательно пройдёт через свою начальную точку!

Книга Тоффоли-Маргополуса
«Машины клеточных автоматов»

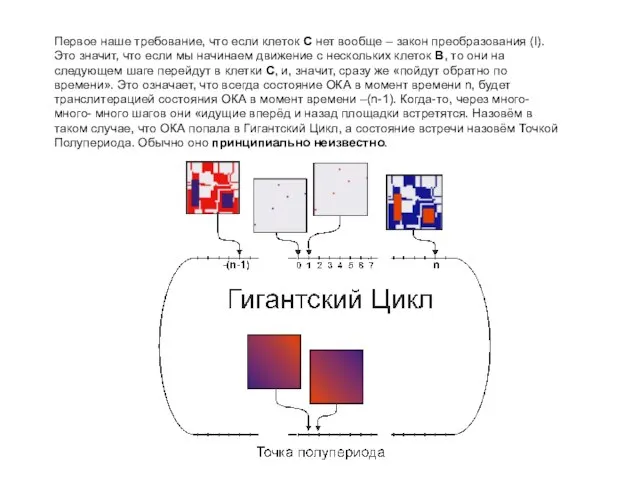
Первое наше требование, что если клеток С нет вообще – закон преобразования (I).
Это значит, что если мы начинаем движение с нескольких клеток B, то они на
следующем шаге перейдут в клетки С, и, значит, сразу же «пойдут обратно по
времени». Это означает, что всегда состояние ОКА в момент времени n, будет
транслитерацией состояния ОКА в момент времени –(n-1). Когда-то, через много-
много- много шагов они «идущие вперёд и назад площадки встретятся. Назовём в
таком случае, что ОКА попала в Гигантский Цикл, а состояние встречи назовём Точкой
Полупериода. Обычно оно принципиально неизвестно.

3. Наши «стандартные» ОКА, описание и программа.
(Цель программы (была) чисто развлекательная. Придумать такую
программу, которая по щелчку мыши генерила бы случайные ОКА,
(отсекая внутри себя откровенно неинтересные), и выводила на экран
результаты их работы. «Жмёшь, жмёшь… интересные записываешь»).
Что нужно для работы...
1) Задать размер квадратной площадки (в нашем случае = 131) и определить замыкается она в
тор или окружена «замороженными А» клетками
2) Задать ОКА («как», описано ниже)
3) Задать начальные условия (несколько случайных клеток В, или одну)
4) Задать «период» - стробоскоп с которым мы будем рассматривать своё иэображение
и нажать кнопку GO!
(+ служба случайного поиска наших «интересных» ОКА)
Всё это есть в нашей программе)
Ещё в любой момент можно «обратить время», поставить на ОКА кластер любых клеток,
кластер «замороженных А» клеток и т.д.

«Стабильные» ОКА. («Улучшение» их).

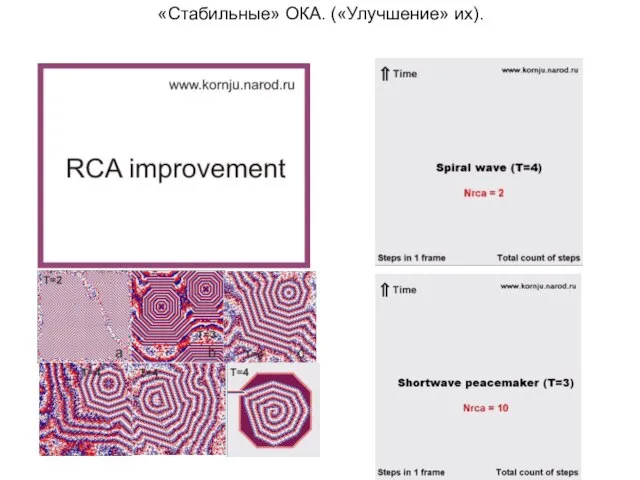
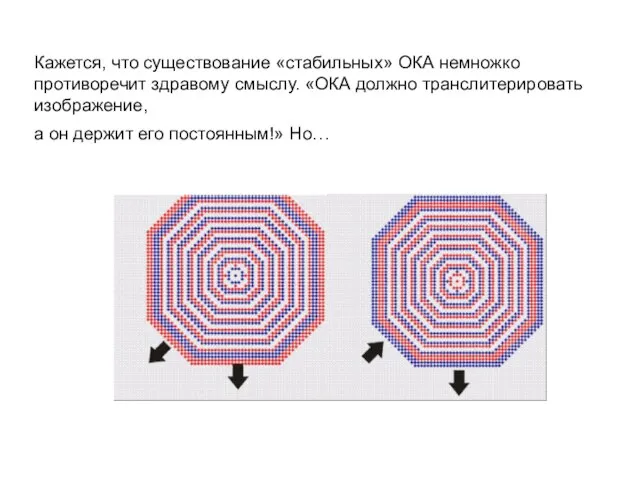
Кажется, что существование «стабильных» ОКА немножко противоречит здравому смыслу. «ОКА должно транслитерировать изображение,
а он держит его постоянным!» Но…

«Эксклюзивные» ОКА

Забавная реакция на возмущение.
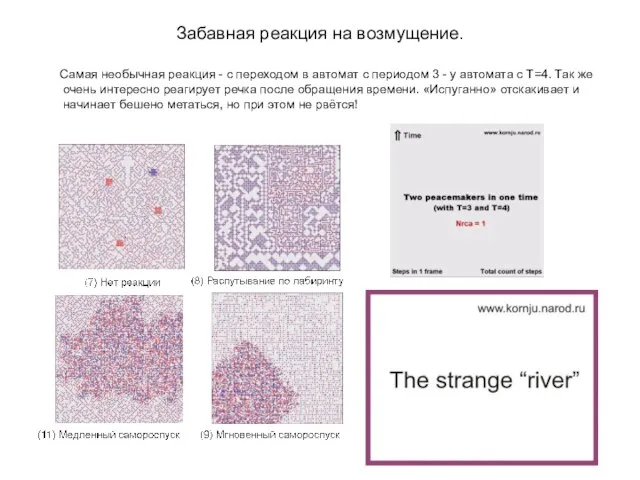
Самая необычная реакция - с переходом в автомат с периодом 3 - у автомата с Т=4. Так же очень интересно реагирует речка после обращения времени. «Испуганно» отскакивает и начинает бешено метаться, но при этом не рвётся!

Интересная реакция на «замороженные А»

Резюме.
У обратимых автоматов есть своя «фишка». Они всегда возвращаются в своё начальное состояние!
Но, вместе с тем, обратимые автоматы обладают и врождённым дефектом! (Эта «фищка», так сказать, недостижима!) Все они при своей работе обязаны «умереть» в Гигантском Цикле. И НИКОГДА, за исключением тривиальных симметричных случаев не смогут быстро вернуться в него.

И, значит «сути» у них – нет! (Отмечено у Тоффоли- Маргополуса!)
…
Итак… все ОКА делают одно и тоже! Уходят в Гигантский Цикл, превращая «порядок» в «беспорядок». Увеличивают энтропию.
А может ли существовать «антиэнтропийный» ОКА. Который превращает «беспорядок» в «порядок»? И здравый смысл, и всё, что мы знаем о «математической природе» однозначно говорят, что это НЕВОЗМОЖНО!
Создать подобный ОКА НЕЛЬЗЯ!!
…
Но… если нельзя, но очень хочется?..

4. «ОКА с периодом 6».
Ничто не может сравнится с «самым простым случаем». Все R=1.
Если сделать это сделать, то произойдёт… чудо!