Обобщающий урок по теме:«Теорема Пифагора»

Значение теоремы Пифагора
Из теоремы Пифагора или с её помощью можно вывести большинство теорем геометрии.
Пребудет вечной истина, как скоро
Её познает слабый человек!
И ныне теорема Пифагора верна,
Как и в его далёкий век.
А.Шамиссо

Пифагоровы
тройки
числа
треугольники
Х2+У2=Z2
3, 4, 5
6, 8, 10
7, 24, 25
8, 15, 17
а
с
в
а2+в2=с2
египетский
3, 4, 5

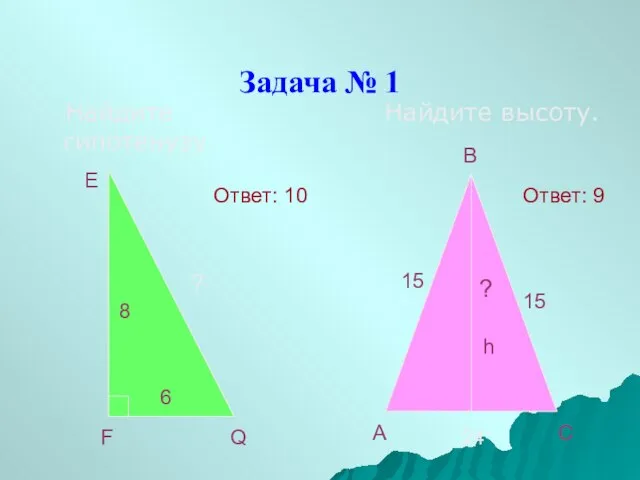
Задача № 1
Найдите гипотенузу.
Найдите высоту.
E
F
Q
8
6
?
B
A
C
15
15
24
?
h Ответ: 10
Ответ: 9

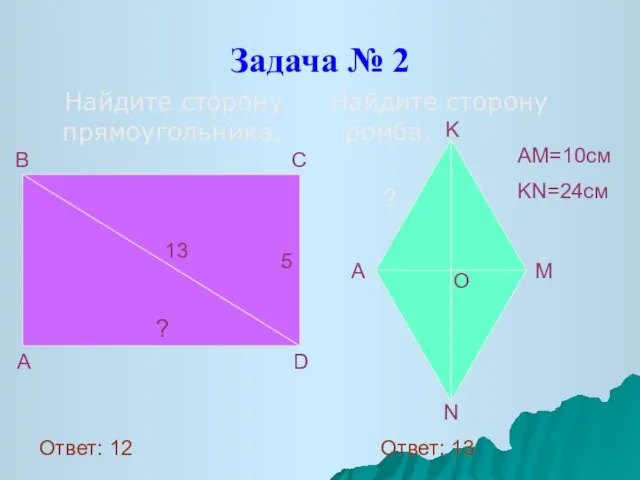
Задача № 2
Найдите сторону прямоугольника.
Найдите сторону ромба.
13
5
?
A D
B
C
O
K
A
M
N
?
AM=10см
KN=24см
Ответ: 12 Ответ: 13

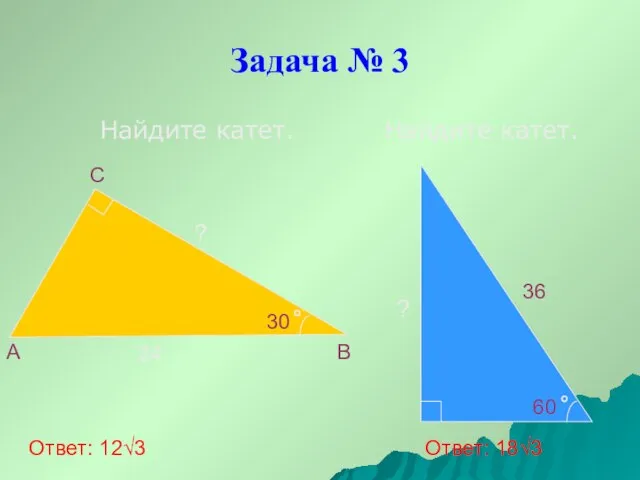
Задача № 3
Найдите катет.
Найдите катет.
A
B
C
24
30
60
36
?
Ответ: 12√3 Ответ: 18√3
?

Задача о бамбуке
из древнекитайского трактата «Гоу-гу»
Имеется бамбук высотой
в 1 чжан. Вершину его со-
гнули так, что она касает-
ся земли на расстоянии
3 чи от корня. Какова вы-
сота бамбука после сгиба-
ния?
1 чжан=10 чи
Ответ: 4,55 чи

Задача индийского математика ХII века Бхаскары
На берегу реки рос тополь одинокий.
Вдруг ветра порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С теченьем реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки.
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?
.

Задача о лотосе
из сочинения Бхаскары (XII век)
На стебле с полфута над озером
тихим,
Рос лотоса цвет.
Он рос одиноко. И ветер порывом
Отнёс его в сторону. Нет
Больше цветка над водой.
Нашёл же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода здесь глубока?
Ответ: 3,75

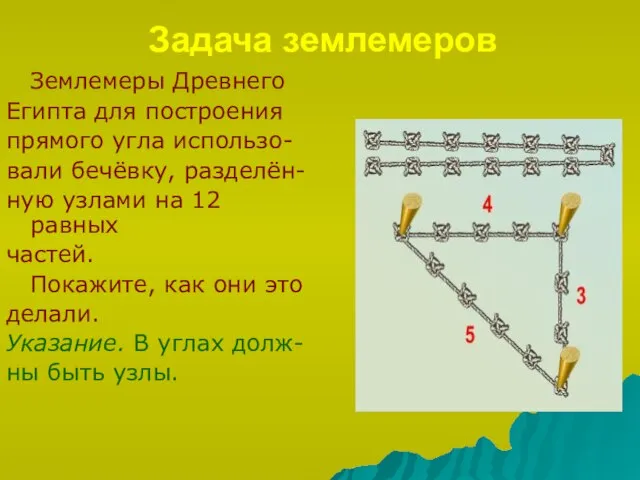
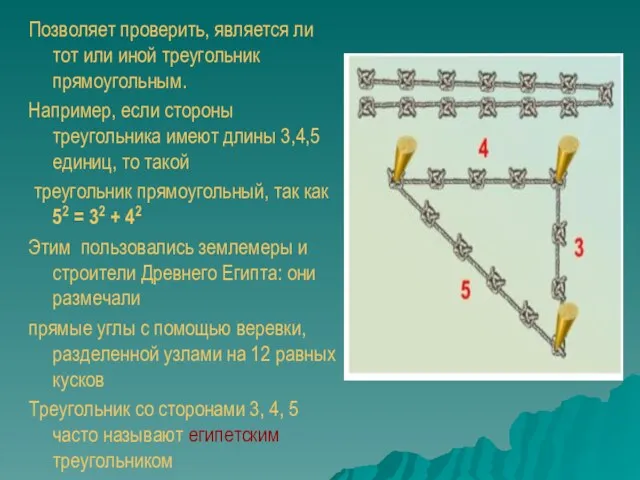
Задача землемеров
Землемеры Древнего
Египта для построения
прямого угла использо-
вали бечёвку, разделён-
ную узлами на 12 равных
частей.
Покажите, как они это
делали.
Указание. В углах долж-
ны быть узлы.

Позволяет проверить, является ли тот или иной треугольник прямоугольным.
Например, если стороны треугольника имеют длины 3,4,5 единиц, то такой
треугольник прямоугольный, так как 52 = 32 + 42
Этим пользовались землемеры и строители Древнего Египта: они размечали
прямые углы с помощью веревки, разделенной узлами на 12 равных кусков
Треугольник со сторонами 3, 4, 5 часто называют египетским треугольником