Содержание
- 2. Задача №1. Решим следующее неравенство методом интервалов: (x+3)2(x2+x+1) ≥ 0 (4-x)x
- 4. Описанный выше метод с небольшими изменениями может быть использован не только для решения рациональных неравенств, но
- 5. Задача №2. Решим неравенство: Алгоритм решения неравенств: 1. ОДЗ 2. Нули функции (т.е. нули числителя и
- 14. Скачать презентацию




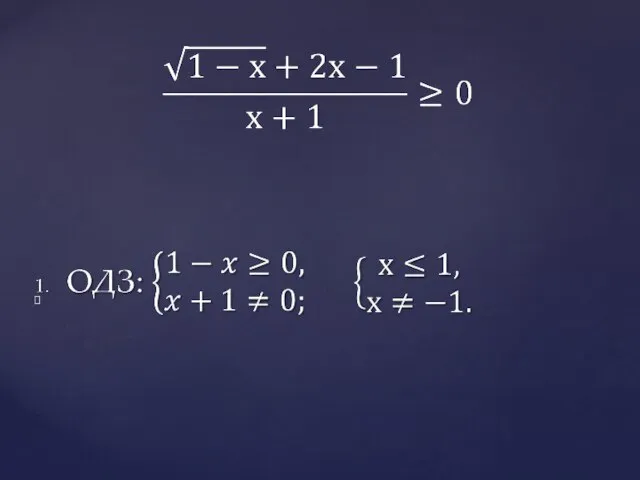
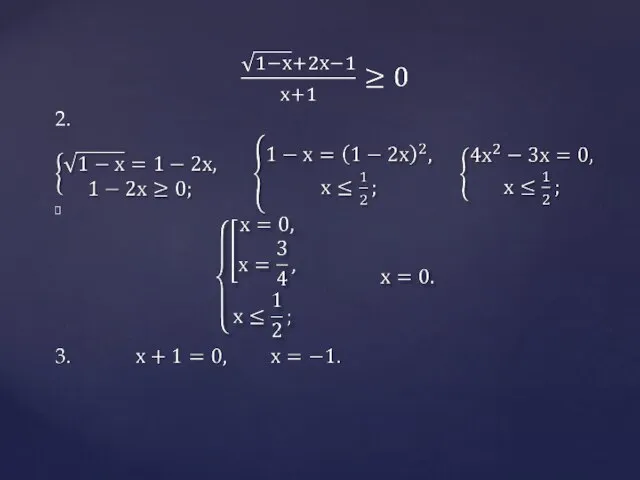





 Вводный инструктаж по технике безопасности на уроках физической культуры
Вводный инструктаж по технике безопасности на уроках физической культуры ВПР по математике 5 класс
ВПР по математике 5 класс Философия мечты
Философия мечты Неформальные движения молодёжи
Неформальные движения молодёжи Чувство прекрасного
Чувство прекрасного Концептуальные основы корпоративной социальной ответственности
Концептуальные основы корпоративной социальной ответственности  Потолочная система охлаждения панельного типа Uponor Comfort
Потолочная система охлаждения панельного типа Uponor Comfort Тема 1.1.Организация производства как система научных знаний
Тема 1.1.Организация производства как система научных знаний Кафтан Урок №4
Кафтан Урок №4 Көксерек в театре
Көксерек в театре Моря Атлантического океана
Моря Атлантического океана Сходство и различие фразеологизмов и пословиц
Сходство и различие фразеологизмов и пословиц Кинесика как составной элемент невербальной коммуникации
Кинесика как составной элемент невербальной коммуникации Правовое регулирование оборота земель сельскохозяйственного назначения
Правовое регулирование оборота земель сельскохозяйственного назначения Гражданственность
Гражданственность Естественный ядерный реактор Окло
Естественный ядерный реактор Окло Презентация на тему Реки России
Презентация на тему Реки России План местности. Условные знаки
План местности. Условные знаки 10 години в 10 минути Христина Машкова “Четиринадесети рекламен форум”
10 години в 10 минути Христина Машкова “Четиринадесети рекламен форум” Моё блюдо: Яичница с овощами
Моё блюдо: Яичница с овощами Энде Михаэль Андреас Гельмут 1929-1995
Энде Михаэль Андреас Гельмут 1929-1995 Изменение состояния региональной гемодинамики у больных с ОАСНК с различной тяжестью ишемии нижних конечностей при лечении мето
Изменение состояния региональной гемодинамики у больных с ОАСНК с различной тяжестью ишемии нижних конечностей при лечении мето Русская кухня
Русская кухня Решение задач
Решение задач Исследование статической устойчивости асинхронной нагрузки при питании их от шин бесконечной мощности
Исследование статической устойчивости асинхронной нагрузки при питании их от шин бесконечной мощности Презентация на тему Инфаркт миокарда
Презентация на тему Инфаркт миокарда  Lecture 1
Lecture 1 Правда или ложь
Правда или ложь