ОБЪЕМ ПРИЗМЫ.Решение задач.

Цель урока:
-обучить решению задач на вычисление объема призм, обобщить и систематизировать имеющиеся у учащихся сведения о призме и ее элементах, формировать умения решать задачи повышенной сложности;
-развивать логическое мышление, умение самостоятельно работать, навыки взаимоконтроля и самоконтроля, умение говорить и слушать;
-выработать привычку к постоянной занятости каким- либо полезным делом, воспитание отзывчивости, трудолюбия, аккуратности.

САМОКОНКОЛЬ И ВЗАИМОКОНТРОЛЬ
Класс Фамилия имя Основные линейные элементы: max 8
С помощью рисунка назовите: max 8 Домашнее задание max 10
Задачи max 8
Тест max10
Итоговая Оценка
11 «В»
Иванова Варвара
7
7
7
8
8
37
Оценка 8,4=8

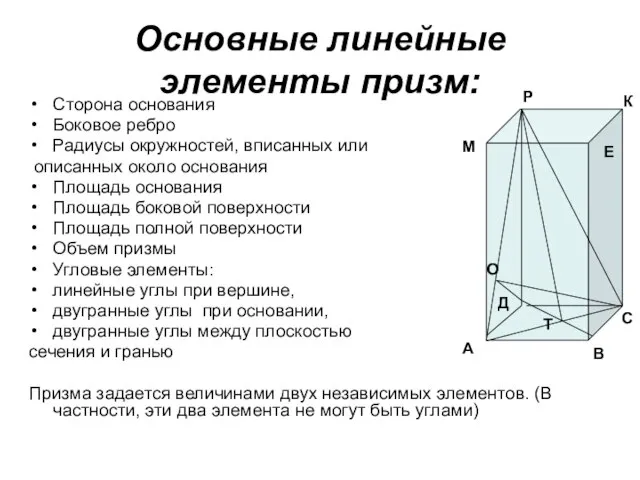
Основные линейные элементы призм:
Сторона основания
Боковое ребро
Радиусы окружностей, вписанных или
описанных около основания
Площадь основания
Площадь боковой поверхности
Площадь полной поверхности
Объем призмы
Угловые элементы:
линейные углы при вершине,
двугранные углы при основании,
двугранные углы между плоскостью
сечения и гранью
Призма задается величинами двух независимых элементов. (В частности, эти два элемента не могут быть углами)
А
В
С
Д
М
Р
К
Е
Т
О

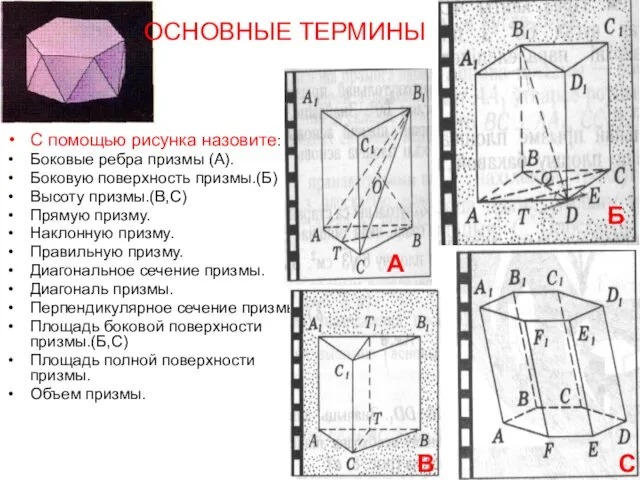
С помощью рисунка назовите:
Боковые ребра призмы (А).
Боковую поверхность призмы.(Б)
Высоту призмы.(В,С)
Прямую призму.
Наклонную призму.
Правильную призму.
Диагональное сечение призмы.
Диагональ призмы.
Перпендикулярное сечение призмы.
Площадь боковой поверхности призмы.(Б,С)
Площадь полной поверхности призмы.
Объем призмы.
ОСНОВНЫЕ ТЕРМИНЫ
А
Б
В
С

ОБЪЕМ ПРИЗМЫ
Теорема.
Объем призмы равен произведению площади основания на высоту.
Следствие.
Объем прямой призмы равен произведению площади основания на длину бокового ребра:V=Sосн∙b (Sосн -площадь основания, b- длина бокового ребра)

ПРОВЕРКА
ДОМАШНЕГО ЗАДАНИЯ
Обменяйтесь тетрадями, проверьте
и выставьте отметку

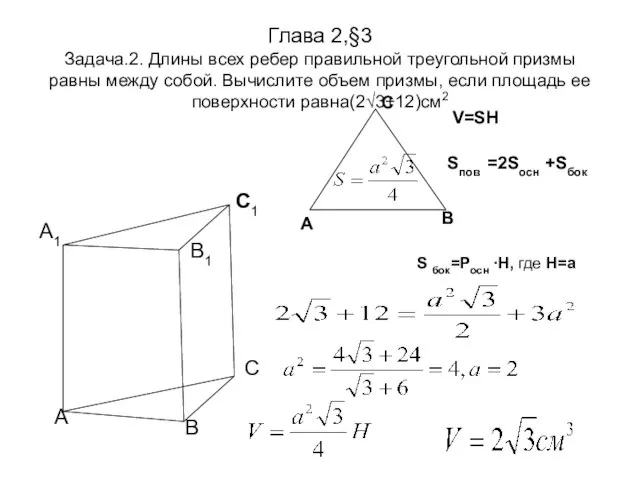
Глава 2,§3
Задача.2. Длины всех ребер правильной треугольной призмы равны между собой. Вычислите объем призмы, если площадь ее поверхности равна(2√3+12)cм2
А
B
C
A1
B1
C1
Sпов =2Sосн +Sбок
А
В
С
S бок=Pосн ∙H, где H=a
V=SH

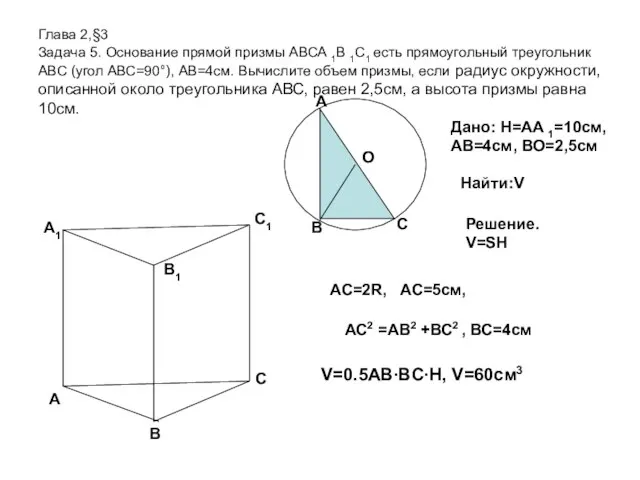
Глава 2,§3
Задача 5. Основание прямой призмы АВСА 1В 1С1 есть прямоугольный треугольник АВС (угол АВС=90°), АВ=4см. Вычислите объем призмы, если радиус окружности, описанной около треугольника АВС, равен 2,5см, а высота призмы равна 10см.
о
А
В
С
А1
В1
С1
А
В
С
О
Дано: H=AA 1=10cм,
АВ=4см, ВО=2,5см
Найти:V
Решение.
V=SH
AC=2R, AC=5cм,
АС2 =АВ2 +ВС2 , ВС=4см
V=0.5AB∙BC∙H, V=60см3

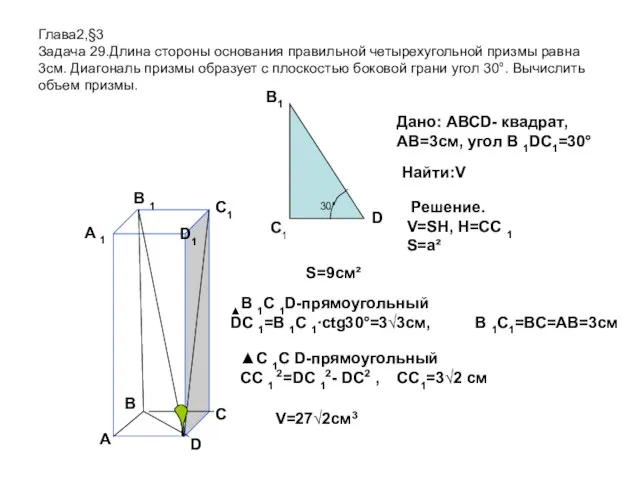
Глава2,§3
Задача 29.Длина стороны основания правильной четырехугольной призмы равна 3см. Диагональ призмы образует с плоскостью боковой грани угол 30°. Вычислить объем призмы.
А
В
С
D
A 1
B 1
C1
D1
C1
B1
D
30°
Дано: АВСD- квадрат, АВ=3см, угол В 1DC1=30°
Найти:V
Решение.
V=SH, H=СС 1
S=a²
S=9cм²
▲В 1С 1D-прямоугольный
DC 1=B 1C 1∙ctg30°=3√3см, В 1С1=ВС=АВ=3см
▲С 1С D-прямоугольный
СC 1 2=DC 12- DC2 , СС1=3√2 см
V=27√2см3

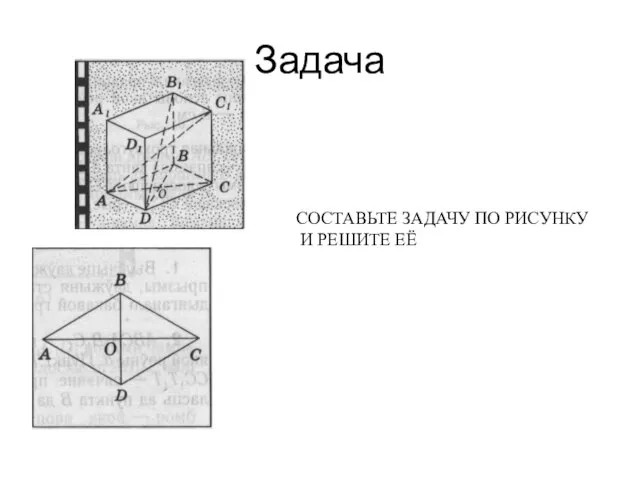
Задача
СОСТАВЬТЕ ЗАДАЧУ ПО РИСУНКУ
И РЕШИТЕ ЕЁ

РЕШЕНИЕ ЗАДАЧ
Глава 2,§3
№ 8 (устно)
№ 9 (устно)
№ 14
№ 30
№ 32

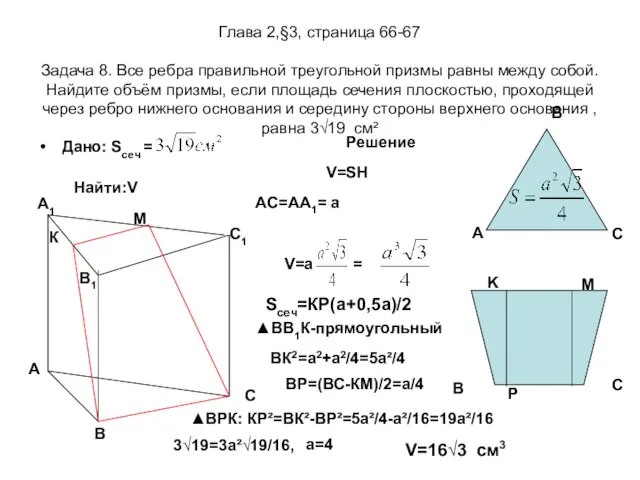
Глава 2,§3, страница 66-67
Задача 8. Все ребра правильной треугольной призмы равны между собой. Найдите объём призмы, если площадь сечения плоскостью, проходящей через ребро нижнего основания и середину стороны верхнего основания , равна 3√19 см²
Дано: Sсеч =
А
В
С
А1
В1
С1
К
М
Найти:V
Решение
V=SH
A
B
C
AC=АА1= a
V=a =
B
K
M
C
P
Sсеч=КР(а+0,5а)/2
▲ВВ1К-прямоугольный
ВК2=а2+а2/4=5а²/4
ВР=(ВС-КМ)/2=а/4
▲ВРК: КР²=ВК²-ВР²=5а²/4-а²/16=19а²/16
3√19=3a²√19/16,
a=4
V=16√3 cм3

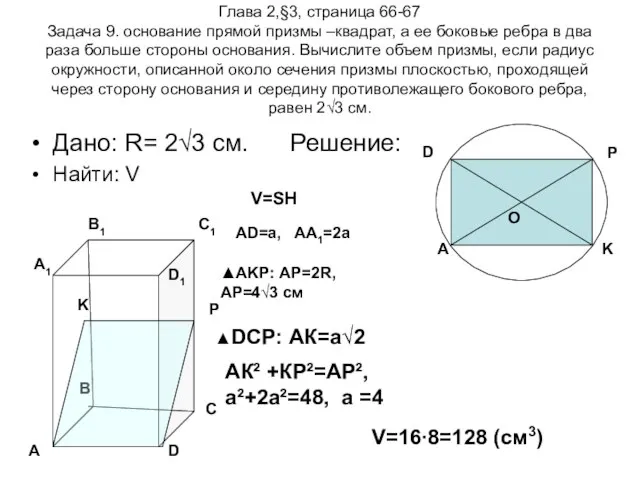
Глава 2,§3, страница 66-67
Задача 9. основание прямой призмы –квадрат, а ее боковые ребра в два раза больше стороны основания. Вычислите объем призмы, если радиус окружности, описанной около сечения призмы плоскостью, проходящей через сторону основания и середину противолежащего бокового ребра, равен 2√3 см.
Дано: R= 2√3 см. Решение:
Найти: V
А
В
С
D
A1
B1
C1
D1
K
P
V=SH
А
D
P
K
O
AD=a, AA1=2a
▲AKP: АР=2R,
АР=4√3 см
▲DCP: АК=a√2
АК² +КР²=АР²,
а²+2а²=48, a =4
V=16∙8=128 (см3)

ФИЗКУЛЬТМИНУТКА

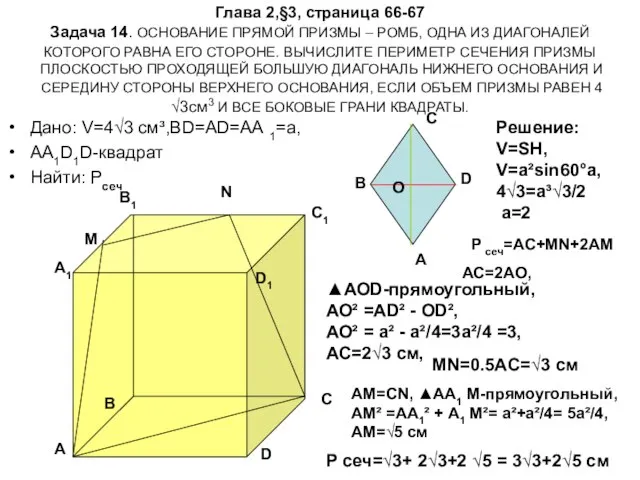
Глава 2,§3, страница 66-67
Задача 14. ОСНОВАНИЕ ПРЯМОЙ ПРИЗМЫ – РОМБ, ОДНА ИЗ ДИАГОНАЛЕЙ КОТОРОГО РАВНА ЕГО СТОРОНЕ. ВЫЧИСЛИТЕ ПЕРИМЕТР СЕЧЕНИЯ ПРИЗМЫ ПЛОСКОСТЬЮ ПРОХОДЯЩЕЙ БОЛЬШУЮ ДИАГОНАЛЬ НИЖНЕГО ОСНОВАНИЯ И СЕРЕДИНУ СТОРОНЫ ВЕРХНЕГО ОСНОВАНИЯ, ЕСЛИ ОБЪЕМ ПРИЗМЫ РАВЕН 4 √3см3 И ВСЕ БОКОВЫЕ ГРАНИ КВАДРАТЫ.
A
B
C
D
A1
B1
C1
D1
A
B
C
D
Дано: V=4√3 см³,BD=AD=АА 1=а,
AA1D1D-квадрат
Найти: Рсеч
M
N
Решение:
V=SH,
V=a²sin60°a,
4√3=a³√3/2
a=2
P сеч=AC+MN+2AM
АС=2АО,
О
▲АОD-прямоугольный,
АО² =АD² - ОD²,
АО² = а² - а²/4=3а²/4 =3,
АС=2√3 см,
MN=0.5AC=√3 см
AM=CN, ▲AA1 M-прямоугольный,
АМ² =АА1² + А1 М²= а²+а²/4= 5а²/4,
АМ=√5 см
P сеч=√3+ 2√3+2 √5 = 3√3+2√5 см

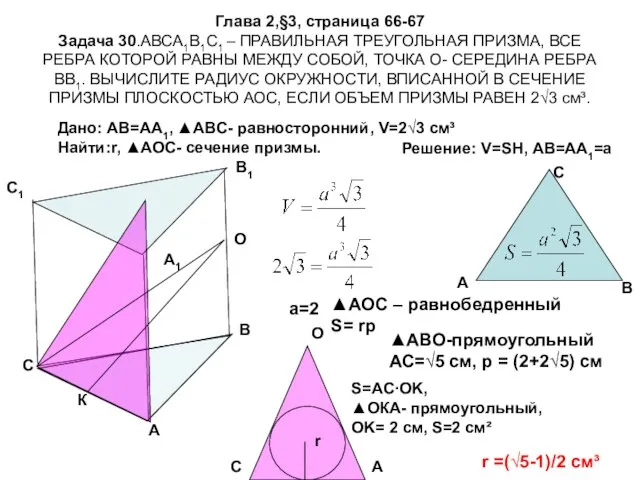
Глава 2,§3, страница 66-67
Задача 30.АВСА1В1С1 – ПРАВИЛЬНАЯ ТРЕУГОЛЬНАЯ ПРИЗМА, ВСЕ РЕБРА КОТОРОЙ РАВНЫ МЕЖДУ СОБОЙ, ТОЧКА О- СЕРЕДИНА РЕБРА ВВ1. ВЫЧИСЛИТЕ РАДИУС ОКРУЖНОСТИ, ВПИСАННОЙ В СЕЧЕНИЕ ПРИЗМЫ ПЛОСКОСТЬЮ АОС, ЕСЛИ ОБЪЕМ ПРИЗМЫ РАВЕН 2√3 см³.
А
В
С
А1
В1
С1
О
Дано: АВ=АА1, ▲АВС- равносторонний, V=2√3 cм³
Найти:r, ▲АОС- сечение призмы.
Решение: V=SH, АВ=АА1=а
A
B
C
a=2
А
С
О
r
▲АОС – равнобедренный
S= rp
▲ABO-прямоугольный
АС=√5 см, р = (2+2√5) см
К
S=AC∙OK,
▲ОКА- прямоугольный,
OK= 2 см, S=2 cм²
r =(√5-1)/2 cм³

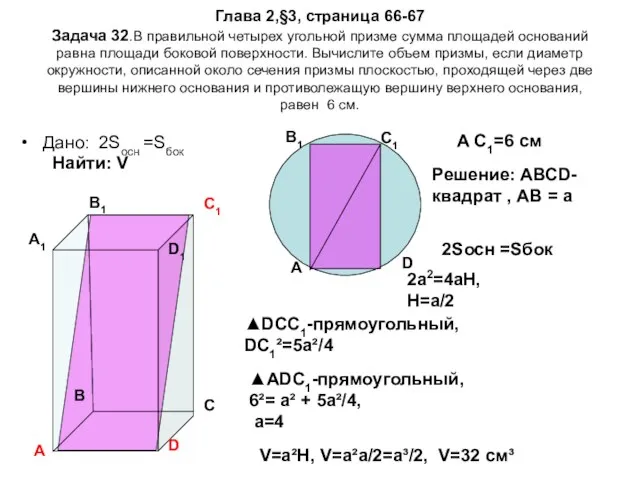
Глава 2,§3, страница 66-67
Задача 32.В правильной четырех угольной призме сумма площадей оснований равна площади боковой поверхности. Вычислите объем призмы, если диаметр окружности, описанной около сечения призмы плоскостью, проходящей через две вершины нижнего основания и противолежащую вершину верхнего основания, равен 6 см.
Дано: 2Sосн =Sбок
А
В
С
D
A1
B1
C1
D1
А
D
C1
B1
A C1=6 см
Решение: АВСD-квадрат , АВ = а
2Sосн =Sбок
2а2=4аH,
H=a/2
▲DCC1-прямоугольный,
DC1²=5a²/4
▲ADC1-прямоугольный,
6²= а² + 5a²/4,
а=4
V=a²H, V=a²a/2=a³/2, V=32 см³
Найти: V

ПРОВЕРЬ СВОИ ЗНАНИЯ
Работа с тестом за компьютером.