Оценка трудозатрат при разработке ПО

Оценка трудозатрат
Рассмотрим методы прогнозирования трудозатрат, которые:
Позволяют оценивать трудозатраты на ранних этапах, в условиях неопределенности.
Позволяют учесть влияние рисков в сроках прогнозов.
Снижают влияние тенденции экспертов к систематической недооценке сложности задач.
Дают механизмы проверки достоверности сроков, основанные на метриках.
При этом, практичны и просты в применении.

Оценка вариации сроков
Как учесть неопределенность в прогнозе

Оценка вариации срока
Оценки сроков неточны:
Эксперты часто имеют тенденцию к систематической недооценке сложности;
Присутствие рисков не позволяет дать точных оценок;
Имея единственную оценку нельзя понять, на что заложился эксперт, когда ее давал.
Выход – давать оценки оптимистичного и пессимистичного сценариев.
Critical Chain Project Management
PERT

Метод PERT Estimation
Обрабатывает три экспертных оценки срока.
L - «раньше не справлюсь точно, даже если повезет»;
H - «успею гарантированно, даже если все риски сыграют»;
M – «наиболее вероятно успею»
Формулы PERT:
PERT Estimation (μ) =( L + 4M + H ) / 6
PERT Deviation (σ) = ( H – L ) / 6
Задача уложится в срок μ+σ с вероятностью 72 %.

Основа PERT Estimation
Длительность задачи - случайная величина, имеющая бета-распределение.
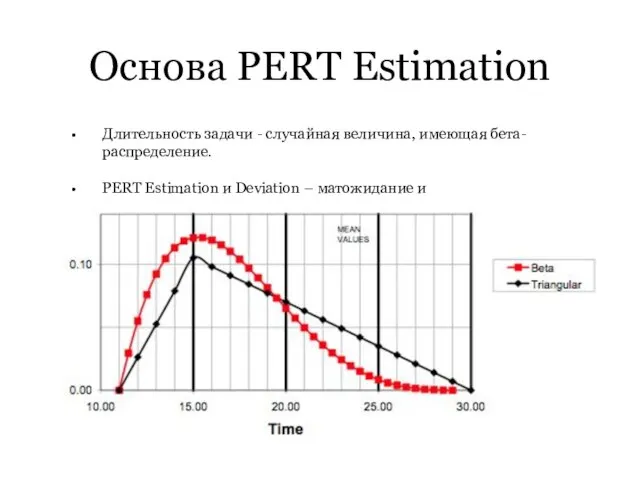
PERT Estimation и Deviation – матожидание и среднеквадратичное отклонение
Между крайними оценками – 6 сигм

Свойства задач с независимыми прогнозами
Для суммы независимых случайных величин верно:
σ = √(σ12 + σ22 + … + σn2)
Сигма суммы независимых случайных величин в процентах уменьшается при увеличении их количества:
Таким образом, чем больше в плане «независимых» задач, тем точнее суммарная оценка сроков. Погрешности планирования разных задач компенсируют друг друга.

Зависимость сигмы от количества задач
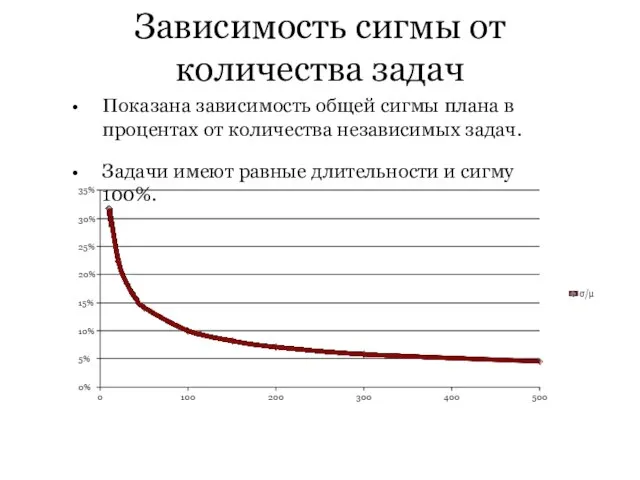
Показана зависимость общей сигмы плана в процентах от количества независимых задач.
Задачи имеют равные длительности и сигму 100%.

Какие задачи независимы?
Независимых задач в разработке много:
Все задачи разработки, которые могут выполняться независимо друг от друга и впараллель;
Все задачи, относящиеся к непересекающемуся функционалу;
Большинство заданий, возникающих при поддержке ПО (исправление дефектов, реализация feature requests, и прочее).
Прогнозы задач зависимы, если их реальные длительности зависят от одних и тех же факторов
Зависимые задачи обычно связанны связью «окончание-начало». Например, фазы разработки зависимы по прогнозу между собой.

Оценки для группы задач
Для суммы случайных величин верно:
μ = μ1 + μ2 + ... + μn;
Ожидаемое время выполнения задач просто суммируется.
Сигма для группы задач:
Суммируется для зависимых прогнозов;
Может быть оценена как корень из суммы квадратов для независимых прогнозов.
Распределение суммы случайных величин меняется, приближаясь к нормальному, при увеличении их количества.
PERT: сумма задач уже не имеет бета-распределения.

Нормальное распределение
«Не справлюсь точно» (вероятность <2%)
= μ - 2σ
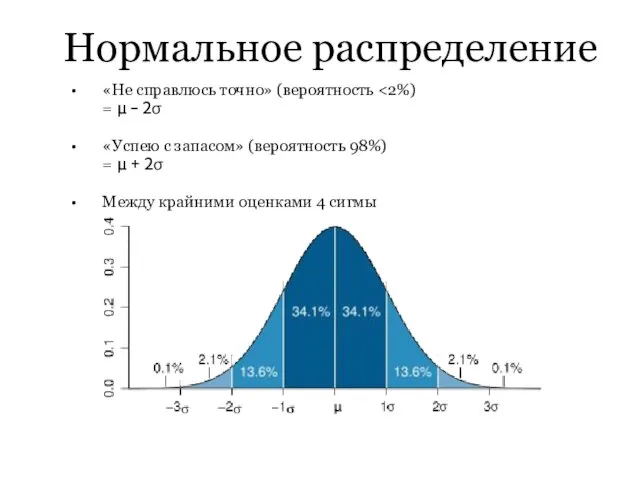
«Успею с запасом» (вероятность 98%)
= μ + 2σ
Между крайними оценками 4 сигмы

PERT Estimation
PERT Deviation лишен внятного смысла для суммы задач.
«Задача уложится в μ+σ с вероятностью 72 %» - для суммы задач уже не верно.
Сколько сигм надо добавить к прогнозу сроков всего проекта, чтобы успеть с вероятностью 85% («скорее всего»)?
PERT Estimation не лучше простой пары оценок «оптимистичная – пессимистичная»
Центральная оценка с весом 4 забивает крайние, и доминирует в прогнозе.
В результате, PERT на практике не позволяет работать с большой неопределенностью в прогнозе.

Модифицируем формулу PERT
В предположении, что срок выполнения задачи имеет нормальное распределение:
«Не справлюсь точно» (вероятность <2%)
= μ - 2σ
«Успею с запасом» (вероятность 98%)
= μ + 2σ
«Normal Estimation»:
μ =( L + H ) / 2
σ = ( H – L ) / 4
Распределение сохраняется при суммировании.
Проект уложится в срок μ+σ c вероятностью ≈85%.

Применение метрик в планировании
Практический подход

Основные метрики
Базовые метрики
Время работы (дни, часы)
Объем работы
Строки кода (SLOC)
Функциональные точки
Количество классов, функций, и т. д.
Количество ошибок
Производные метрики
Продуктивность = Объем / Время
Плотность ошибок = Количество / Объем

Свойства метрик
Базовые метрики дают корелляции
Объем vs Время
Объем vs количество ошибок
Производные метрики устойчивы и колеблются в границах коридора.
Фактические значения метрик с завершенных проектов могут быть измерены и использованы при планировании.
PSP/TSP – пример методологии разработки построенной на применении метрик.

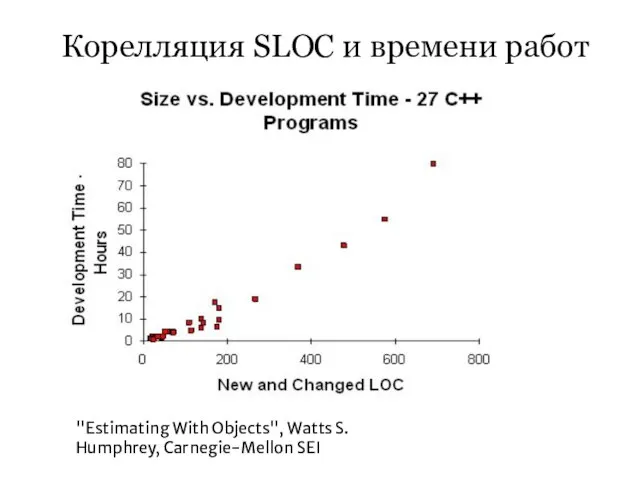
Корелляция SLOC и времени работ
"Estimating With Objects", Watts S. Humphrey, Carnegie-Mellon SEI

Метрика SLOC
Дает лучшие корелляции с временем и количеством ошибок.
Учитываются только те строки, в которых можно допустить ошибки.
Не учитываются комментарии, пустые строки, и автоматически генерируемый код.
Можно не учитывать операторные скобоки (begin-end, { }, прочее).
Может быть посчитана автоматически.
Может быть использована как промежуточная метрика (proxy-based estimation), рассчитанная из других метрик объема (классы, функции, функциональные точки, и т.д.)

Время разработки
Время должно включать в себя все основные активности разработки, на которых вносятся ошибки:
проектирование;
кодирование;
отладка;
а, также, возможно, работу с требованиями.
Корелляции с объемом проявляются:
На законченных проектах;
На задачах, которые могут быть раздельно протестированы.

Метрика «продуктивности»
Осмысленна при наличии корелляции время-объем.
Более стабильна на больших отрезках времени, в том числе и для группы программистов.
Колеблется в некотором коридоре, зависящем от:
языка программирования;
характера и сложности задачи;
стиля программиста – разные люди решают одинаковые задачи с разным размером кода;
качества результата – чем меньше в нем ошибок, тем меньше «продуктивность».
Нельзя применять как показатель эффективности работы.
Программист, тратящий меньше времени на проектирование, и пишущий больше кода для той же задачи – покажет высокую «продуктивность».

Применение в планировании
Получение сроков от оценки объема:
Выполнить прогноз объема в удобной метрике (например – количество модулей или классов)
Перейти к SLOC (proxy-based estimation).
Пользуясь корелляцией SLOC/time, выполнить прогноз времени.
Недостатки
Сложно учесть в прогнозе риски.
Сложно учесть тенденцию экспертов к недооценке сложности.
Требуется аккуратно подойти к выбору базы для снятия метрик.
Альтернатива:
Выполнить раздельный прогноз сроков и объема
Использовать «продуктивность» как проверочный коэффициент

Правила проверки
Метрика «продуктивности» должна находится в коридоре исторических колебаний по аналогичным завершенным проектам.
Вылет за коридор чаще всего означает грубую ошибку в прогнозе срока или объема.
«Продуктивность» должна отражать представление о сложности задачи.
Сложная задача не может иметь «продуктивность» у верхней границы коридора, и наоборот.
Для двух задач, одна из которых сложнее другой – «продуктивность» более сложной должна быть меньше.
Невыполнение правила указывает на ошибку в оценках как минимум одной из задач.