Однофазные линейные электрические цепи синусоидального тока. Электродвижущие силы, напряжения и токи
Содержание
- 2. Основные понятия Основные понятия Цепи синусоидального напряжения – электрические величины изменяются по синусоидальному закону. В частности
- 3. Почему применяют синусоидальный ток Основные понятия В практике применяются частоты переменного тока от долей герца до
- 4. Почему применяют синусоидальный ток Основные понятия Почему синусоидальный? Форма кривой периодически изменяющегося переменного тока может быть
- 5. Получение синусоидального напряжения Основные понятия Электротехника и электроника. Лекция 4
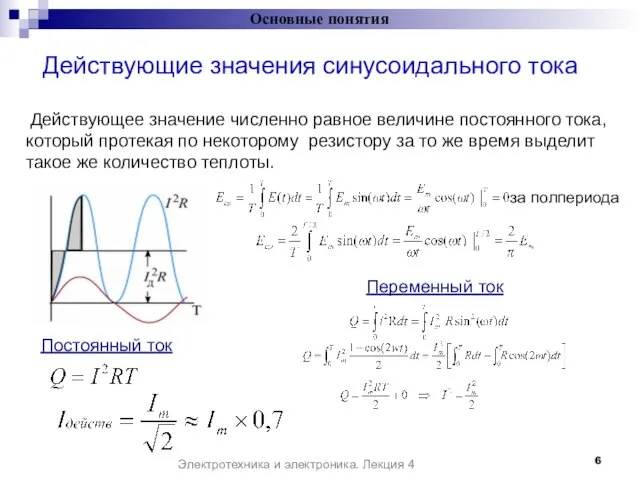
- 6. Действующие значения синусоидального тока Основные понятия Действующее значение численно равное величине постоянного тока, который протекая по
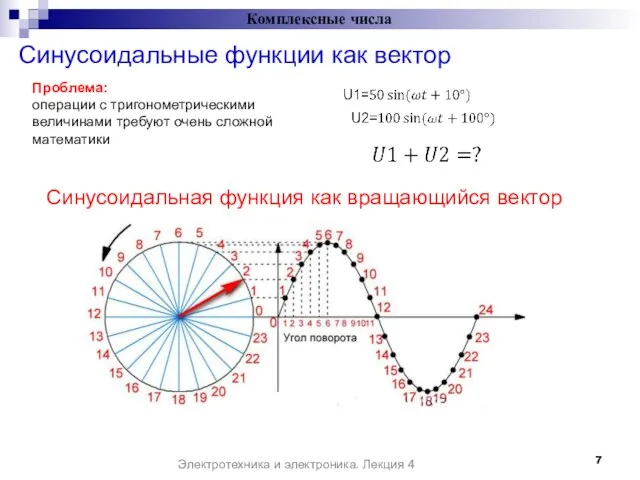
- 7. Комплексные числа Синусоидальная функция как вращающийся вектор Проблема: операции с тригонометрическими величинами требуют очень сложной математики
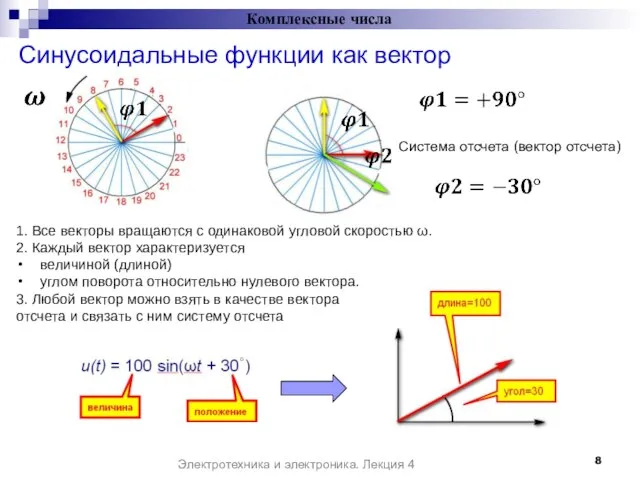
- 8. Комплексные числа Система отсчета (вектор отсчета) 1. Все векторы вращаются с одинаковой угловой скоростью ω. 2.
- 9. Комплексные числа 1. Теперь можно действия над тригонометрическими функциями заменить алгебраическими действиями над комплексными числами. 2.
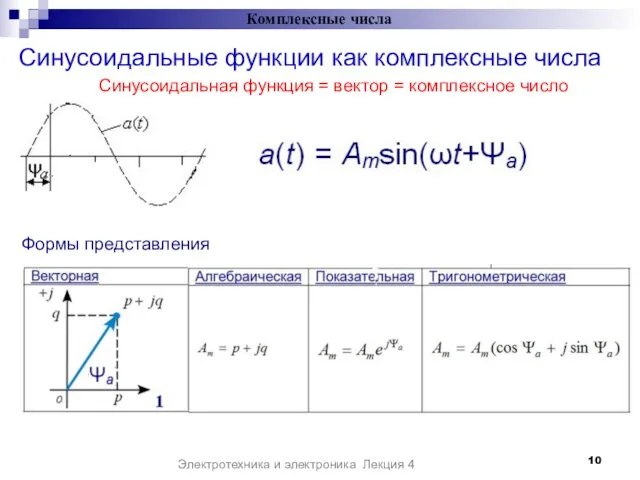
- 10. Синусоидальные функции как комплексные числа Комплексные числа Электротехника и электроника Лекция 4 Формы представления Синусоидальная функция
- 11. Связь между формами комплексных чисел Комплексные числа Векторная Алгебраическая Показательная Электротехника и электроника. Лекция 4
- 12. Действия над комплексными числами Комплексные числа Электротехника и электроника. Лекция 4
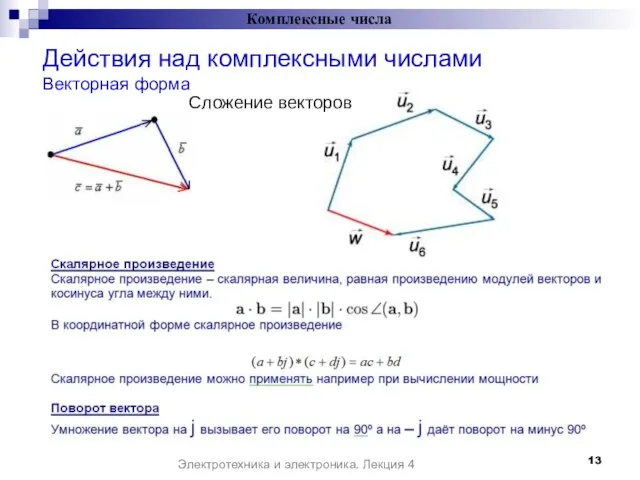
- 13. Действия над комплексными числами Векторная форма Комплексные числа Сложение векторов Электротехника и электроника. Лекция 4
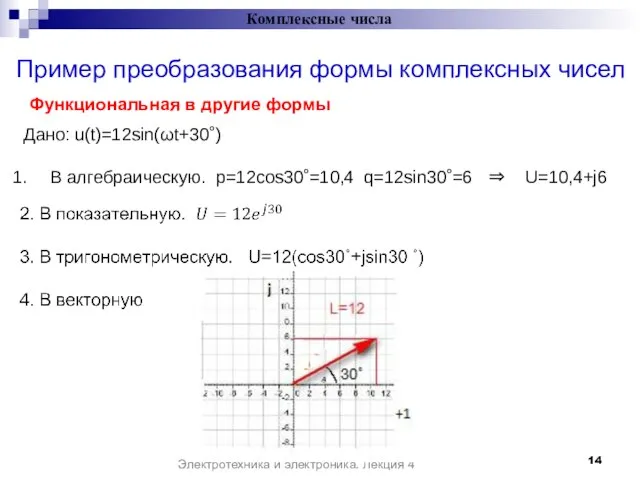
- 14. Пример преобразования формы комплексных чисел Комплексные числа Электротехника и электроника. Лекция 4 Дано: u(t)=12sin(ωt+30˚) В алгебраическую.
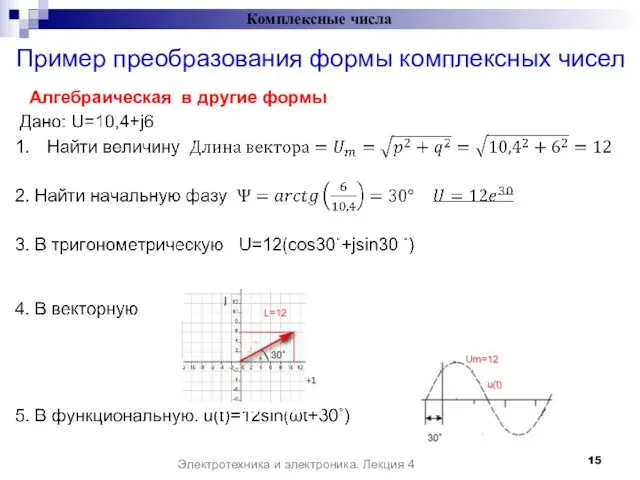
- 15. Пример преобразования формы комплексных чисел Комплексные числа Электротехника и электроника. Лекция 4 Алгебраическая в другие формы
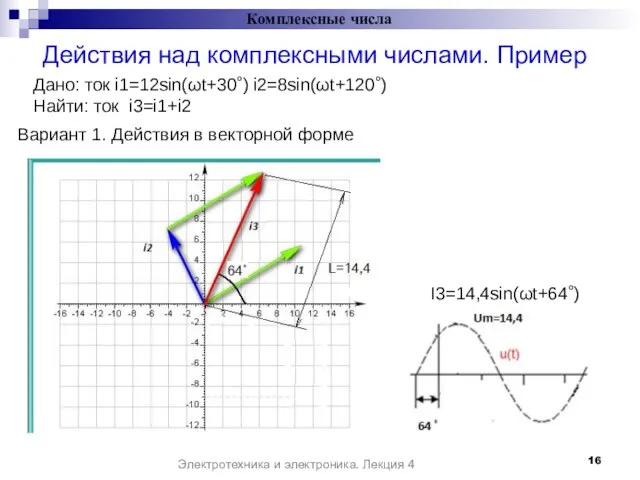
- 16. Действия над комплексными числами. Пример Комплексные числа Электротехника и электроника. Лекция 4 Дано: ток i1=12sin(ωt+30˚) i2=8sin(ωt+120˚)
- 17. Действия над комплексными числами. Пример Комплексные числа Электротехника и электроника. Лекция 4 Дано: ток i1=12sin(ωt+30˚) i2=8sin(ωt+120˚)
- 19. Скачать презентацию








 Мастер украшения помогает сделать праздник
Мастер украшения помогает сделать праздник Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году
Отчет о научно-организационной деятельности Президиума АН РБ в 2009 году Глянец в дизайне. Фотоальбом
Глянец в дизайне. Фотоальбом Проблема адекватности восприятия текста
Проблема адекватности восприятия текста Презентация на тему Оборона Сталинграда
Презентация на тему Оборона Сталинграда  Красная книга России (4 класс)
Красная книга России (4 класс) Введение в техническую графику. Тест
Введение в техническую графику. Тест Этапы проектной деятельности
Этапы проектной деятельности Особенности питания детей грудного возраста
Особенности питания детей грудного возраста До свидания! До новых встреч!
До свидания! До новых встреч! Устройство компьютера
Устройство компьютера Автомат световых эффектов. Схема
Автомат световых эффектов. Схема Изменяющаяся роль медицинских представителей и фармацевтов в аптеках Евгения Домнина Руководитель проектов Москва. 7 декабря 2
Изменяющаяся роль медицинских представителей и фармацевтов в аптеках Евгения Домнина Руководитель проектов Москва. 7 декабря 2 I возрастная ступень комплекса ГТО (от 6 до 8 лет)
I возрастная ступень комплекса ГТО (от 6 до 8 лет) Сказка в картинках - презентация
Сказка в картинках - презентация Презентация на тему Применение солей
Презентация на тему Применение солей Иконопись на Смоленщине
Иконопись на Смоленщине Создание портфолио
Создание портфолио Демократическое правовое государство
Демократическое правовое государство Информационная безопасность в юриспруденции. Лекция №2
Информационная безопасность в юриспруденции. Лекция №2 Роль стандартизации в инновационной сфере
Роль стандартизации в инновационной сфере Дестабилизирующие факторы современности
Дестабилизирующие факторы современности Презентация на тему Сахарный диабет
Презентация на тему Сахарный диабет Литвин, преза, готовая
Литвин, преза, готовая Деньги и инстинкты
Деньги и инстинкты Построение Сечения объемных фигур в Paint
Построение Сечения объемных фигур в Paint Город мечты
Город мечты Страхование строительно-монтажных рисков и послепусковых гарантийных обязательств
Страхование строительно-монтажных рисков и послепусковых гарантийных обязательств