Презентация по физике для проведения урока по теме: R,C,L в цепи переменного тока Вопросы для изучения: Действующие значения тока и
Содержание
- 2. R C L @ Краснополянская школа № 1 Домнин Константин Михайлович 2006 год в цепи переменного
- 3. Действующие значения тока и напряжения. Активное сопротивление в цепи переменного тока
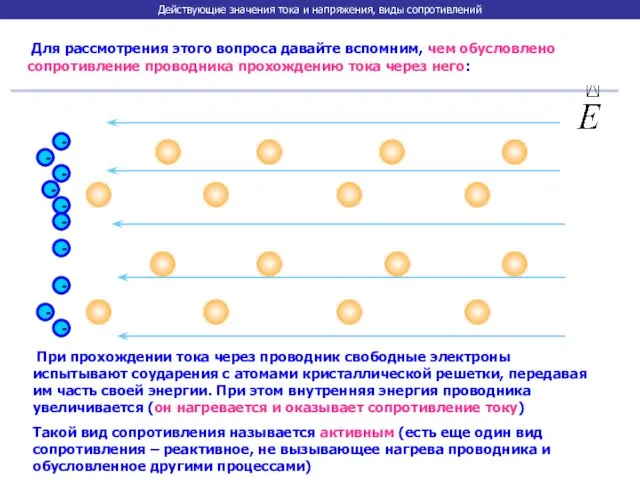
- 4. Действующие значения тока и напряжения, виды сопротивлений Для рассмотрения этого вопроса давайте вспомним, чем обусловлено сопротивление
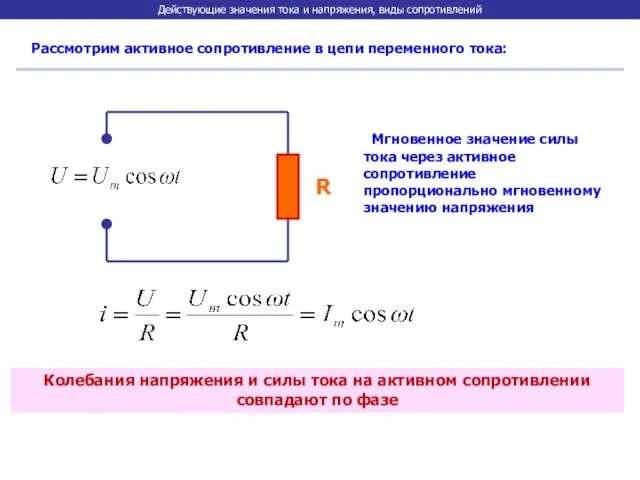
- 5. Действующие значения тока и напряжения, виды сопротивлений Рассмотрим активное сопротивление в цепи переменного тока: R Мгновенное
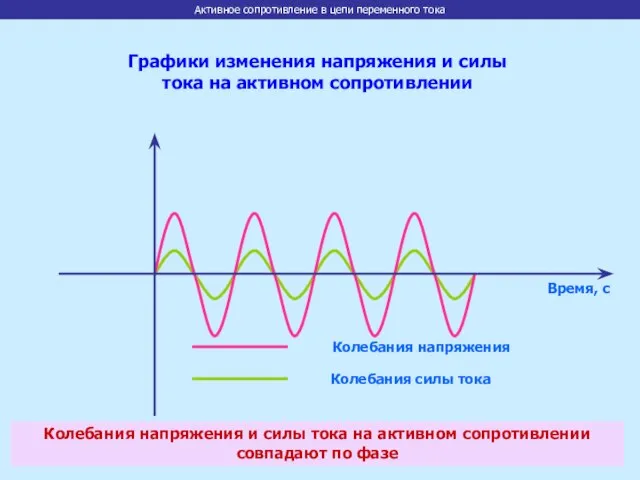
- 6. Время, с Колебания напряжения Колебания силы тока Графики изменения напряжения и силы тока на активном сопротивлении
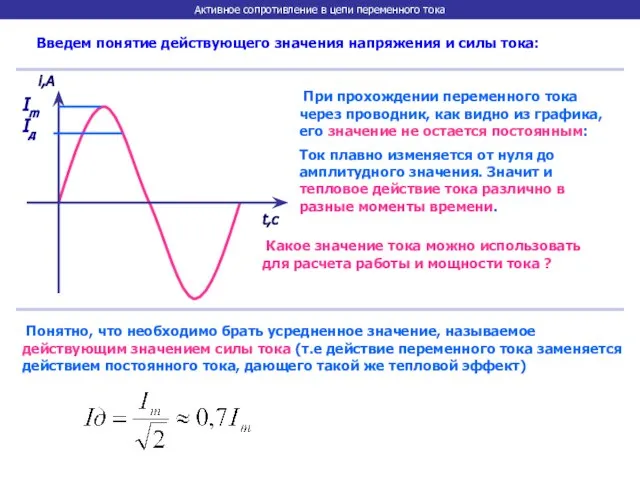
- 7. Активное сопротивление в цепи переменного тока Введем понятие действующего значения напряжения и силы тока: При прохождении
- 8. Активное сопротивление в цепи переменного тока Аналогично действующее значение напряжения: Тогда действующая мощность (средняя мощность): а
- 9. 2. Конденсатор в цепи переменного тока C
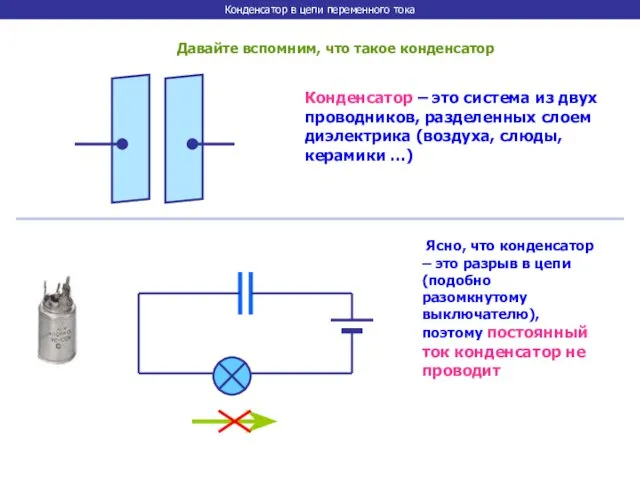
- 10. Конденсатор в цепи переменного тока Давайте вспомним, что такое конденсатор Конденсатор – это система из двух
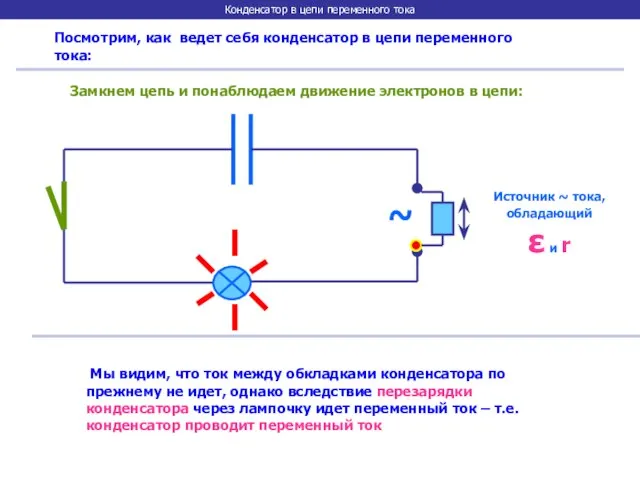
- 11. Конденсатор в цепи переменного тока Посмотрим, как ведет себя конденсатор в цепи переменного тока: ~ Источник
- 12. Конденсатор в цепи переменного тока Итак, конденсатор проводит переменный ток, однако он оказывает току сопротивление, которое
- 13. Конденсатор в цепи переменного тока Проанализируем формулу емкостного сопротивления: Из формулы видно, что сопротивление конденсатора обратно
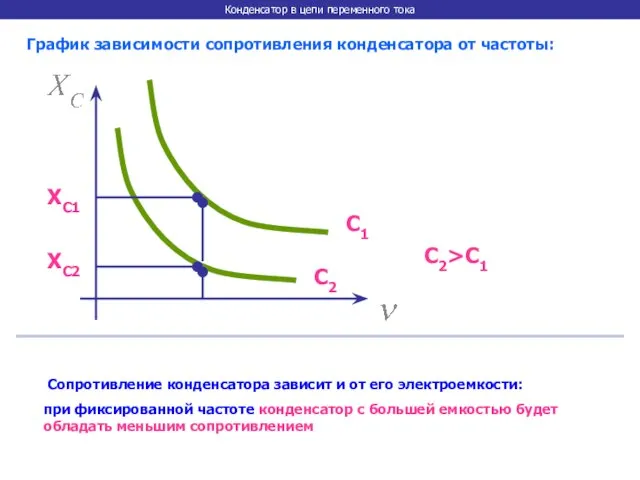
- 14. Конденсатор в цепи переменного тока График зависимости сопротивления конденсатора от частоты: Сопротивление конденсатора зависит и от
- 15. Конденсатор в цепи переменного тока Сдвиг фаз между напряжением и током: Если напряжение на конденсаторе меняется
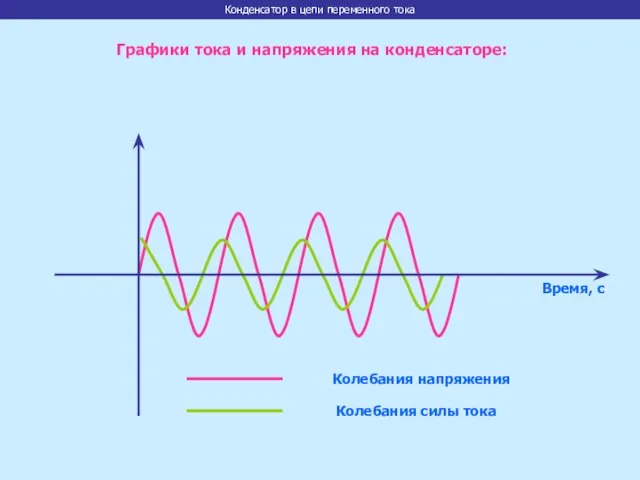
- 16. Время, с Колебания напряжения Колебания силы тока Графики тока и напряжения на конденсаторе: Конденсатор в цепи
- 17. 3. Индуктивность в цепи переменного тока L
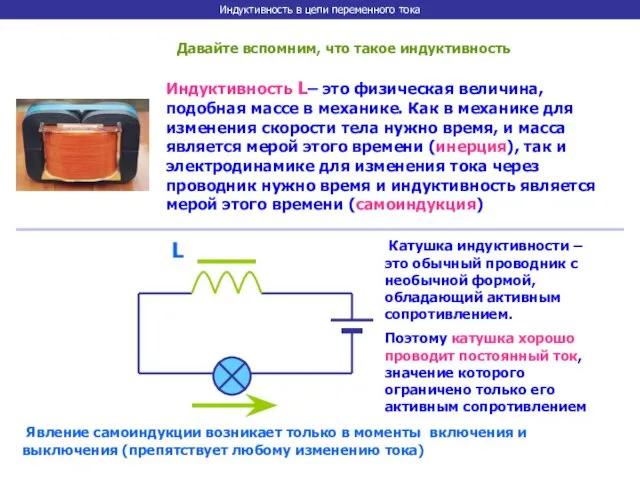
- 18. Индуктивность в цепи переменного тока Давайте вспомним, что такое индуктивность Индуктивность L– это физическая величина, подобная
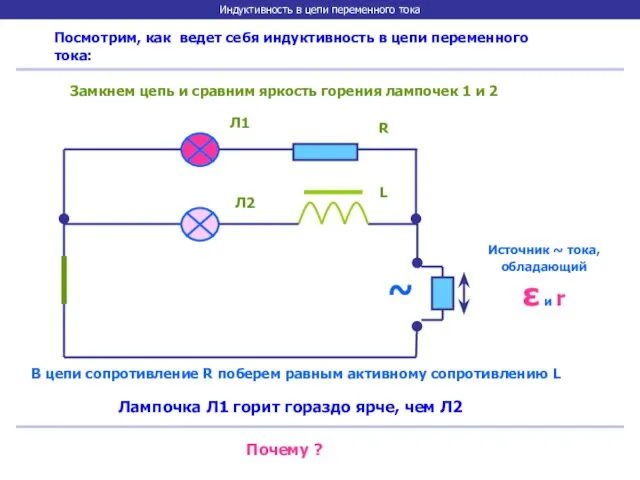
- 19. Индуктивность в цепи переменного тока Посмотрим, как ведет себя индуктивность в цепи переменного тока: ~ Источник
- 20. Индуктивность в цепи переменного тока Все дело в явлении самоиндукции, возникающей в катушке при любом изменении
- 21. Индуктивность в цепи переменного тока Проанализируем формулу индуктивного сопротивления: Из формулы видно, что индуктивное сопротивление прямо
- 22. Сдвиг фаз между напряжением и током: Если ток в катушке изменяется по закону: то напряжение на
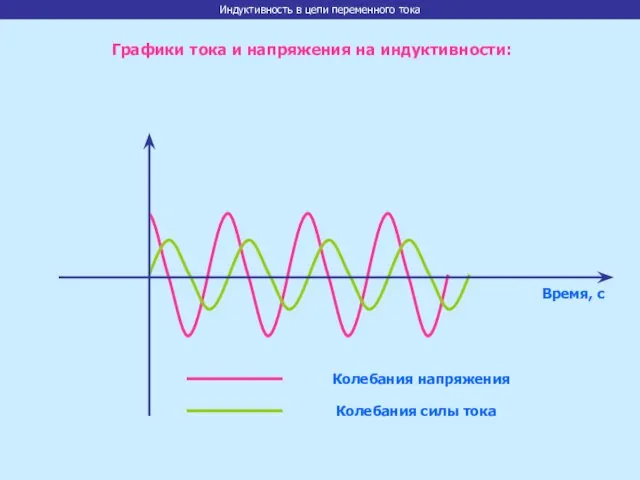
- 23. Время, с Колебания напряжения Колебания силы тока Индуктивность в цепи переменного тока Графики тока и напряжения
- 24. 4. Использование частотных свойств конденсатора и катушки индуктивности
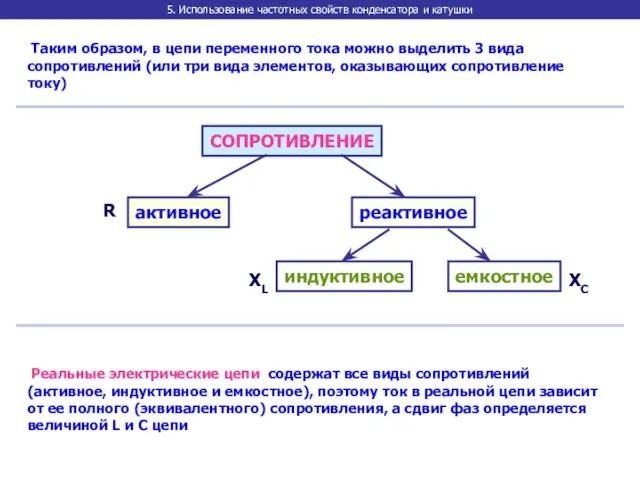
- 25. 5. Использование частотных свойств конденсатора и катушки Таким образом, в цепи переменного тока можно выделить 3
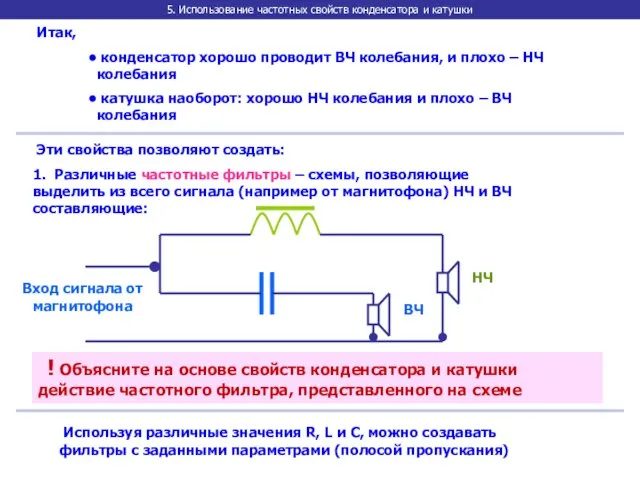
- 26. 5. Использование частотных свойств конденсатора и катушки Итак, конденсатор хорошо проводит ВЧ колебания, и плохо –
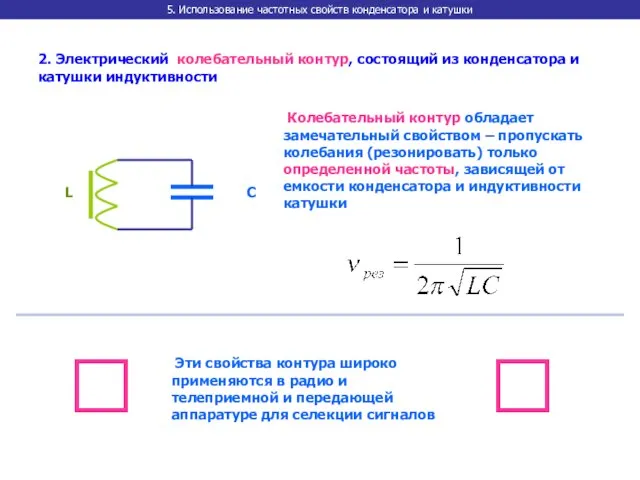
- 27. 5. Использование частотных свойств конденсатора и катушки 2. Электрический колебательный контур, состоящий из конденсатора и катушки
- 28. На этом урок закончен, на следующем уроке мы рассмотрим примеры решения задач на частотные свойства конденсатора
- 30. Скачать презентацию













 «Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами»
«Обзор законодательства Республики Казахстан в сфере социальной поддержки и обеспечения социальными услугами» Роспись петуха по мотивам Филимоновской росписи
Роспись петуха по мотивам Филимоновской росписи Гражданское право. Понятие и виды сроков в гражданском праве
Гражданское право. Понятие и виды сроков в гражданском праве Модернизм
Модернизм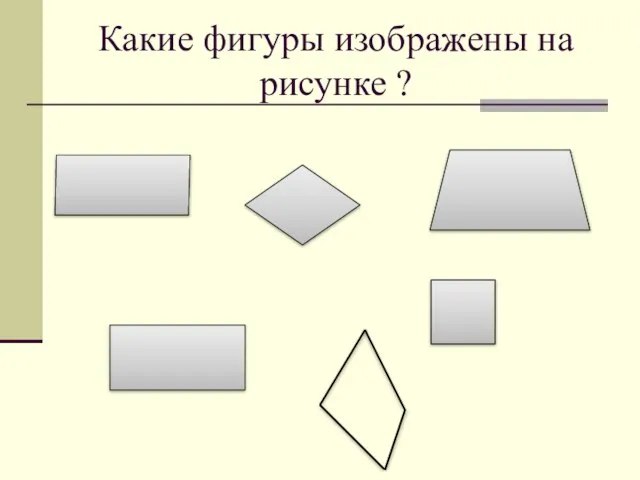 Какие фигуры изображены на рисунке ?
Какие фигуры изображены на рисунке ? Перенос слова переносятся по слогам
Перенос слова переносятся по слогам Принтеры
Принтеры Методическая разработка «Создание презентаций» Элективный курс для 10 класса.
Методическая разработка «Создание презентаций» Элективный курс для 10 класса. Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне
Вейк-лебедка - летний бизнес. Вейкпарк в пляжной зоне Федеральное Собрание РФ
Федеральное Собрание РФ Инжиниринг нефтехимии и нефтегазопереработки
Инжиниринг нефтехимии и нефтегазопереработки Китайский клуб МИИТа
Китайский клуб МИИТа Мой город, с тебя начинается Родина (город Сатка)
Мой город, с тебя начинается Родина (город Сатка) Спартакиада пенсионеров муниципального образования Город Гатчина
Спартакиада пенсионеров муниципального образования Город Гатчина Эры. Основные события органического мира
Эры. Основные события органического мира Презентация на тему Операционные системы на мобильных устройствах
Презентация на тему Операционные системы на мобильных устройствах  Живопись
Живопись Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы
Михайленко Юлия Борисовна учитель начальных классов ГБОУ гимназии № 1518 г. Москвы Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70
Муниципальное общеобразовательное учреждение лингвистическая гимназия № 70 МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942)
МОСКВА- ГОРОД ГЕРОЙ . Битва за Москву(30 сентября 1941- 20 апреля 1942) Векторы в пространстве и не только
Векторы в пространстве и не только Презентация на тему История развития отечественной вычислительной техники
Презентация на тему История развития отечественной вычислительной техники Трансформация изображения через трансформацию формы - серия открыток
Трансформация изображения через трансформацию формы - серия открыток ОРНАМЕНТЫ в национальном костюме
ОРНАМЕНТЫ в национальном костюме Цветник для солнечного места “Степной бриз ”
Цветник для солнечного места “Степной бриз ” Презентация на тему Тургенев. Стихи в прозе
Презентация на тему Тургенев. Стихи в прозе 287 Воскресшему служу я
287 Воскресшему служу я Берлину заменить Северный поток-2 другим проектом
Берлину заменить Северный поток-2 другим проектом