Однопараметрические семейства линий

Найти все точки плоскости ХоY,через которые:
(а) проходит только одна парабола;
(б) не проходит ни одна парабола;
(в) проходит более одной параболы семейства
y=x²+(4p+2)x+2p²

ax+by=p
Например, уравнение
x-2y=p
задает семейство прямых с угловым коэффициентом k=1/2 и пересекающих ось oX в точке (0; - p /2)

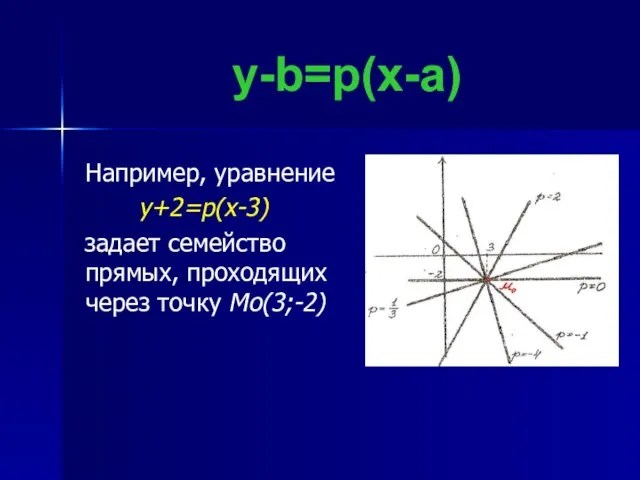
y-b=p(x-a)
Например, уравнение
y+2=p(x-3)
задает семейство прямых, проходящих через точку Mo(3;-2)

(x-a)²+(y-b)²=p
Например, уравнение
x²+2x+y²-6y+p=0<=>(x+1)²+(y-3)²=10-p задает (при p<10) семейство окружностей радиуса R=√10-p с
центром в точке С:(-1;- З)

x²+y²=px
Семейство окружностей радиуса 1/2׀p׀ c центром на оси oX в точке (p /2;0). Все они проходят через начало координат.
Действительно, x²+y²=px<=>(x-p/2)²+y²=p²/2

x²+y²=py
Семейство окружностей радиуса1/2׀p׀ c центром на оси oУ в точке (0; p /2); все они также проходят через начало координат.

(x-a)(y-b)=p
При p=0 уравнение задает пару пересекающихся прямых: x=b и y=p. При p≠0 это две ветви гиперболы-y=b( p/x-a)
Ее асимптотами являются вышеуказанные прямые x=a и y=b точка пересечения которых является их центром симметрии. При р>0 гипербола занимает первую и третью четверти (относительно асимптот),
семейства (x+3)(y+2)=p для значений p=0, p= -4, p=6, p=15.
а при p <0 - вторую и четвертую на рисунке представлены линии

y=f(x-p) y-p=f(x)
Например, (x-p)²+(y-1)²=4 задает семейство окружностей радиуса R=2 с центром в точке С (p;1).
А уравнение у = p-√x+4 семейство «полупарабол», получающихся из графика y= -√x+4 сдвигом по вертикали на p.

y=f(x/p) y/p=f(x)
На рисунке представлено семейство парабол y=p(x²-2x) для значений р=1,p=3,p=1/2, p=-1,p= -2 и p=0 (это прямая у=0).
Все параболы этого семейства пересекают ось оХ при х=0 и x = 2.

Определить вид семейства линий, заданных данными уравнениями, и нарисовать несколько типичных линий
(x+p-2)²+(y-p²/4+1)²=9
семейства, отвечающих конкретным значениям р
Данное уравнение представляет собой окружность радиуса R=3 с центром в точке С с координатами x= -p+2 y=p²/4-1. Исключив из этой системы параметр p , получим уравнение y=1/4(x-2)²-1. Значит, все центры этих окружностей лежат на параболе y=(1/4)x²-x
р=0 (с центром С(2; -1) ), р=2 (с центром С(0;0) ), р=4(с центром С(6;3) ), р=5 (с центром С(-3;5 ¼)).

y= -x²+4px+2-3p-4p²
Ясно, что это параболы с ветвями, направленными вниз:y=-(x-2p)²+2-3p вершина которых V имеет координаты x=2p y=2-3p исключив параметр р из предыдущей системы, получим y=2-3|2x
Т. е. все вершины парабол лежат на Прямой y=2-3|2 x.Поскольку
коэффициент при х² постоянен (равен -1), то все параболы имеют одинаковую форму, т.е. получаются друг из ,друга параллельным переносом.
Здесь представлены параболы семейства при
р=0, р=4 и р= -2.